Distribute Coins in Binary Tree

Problem

You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.

In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.

Return the minimum number of moves required to make every node have exactly one coin.

Examples

Example 1:

1
2
3

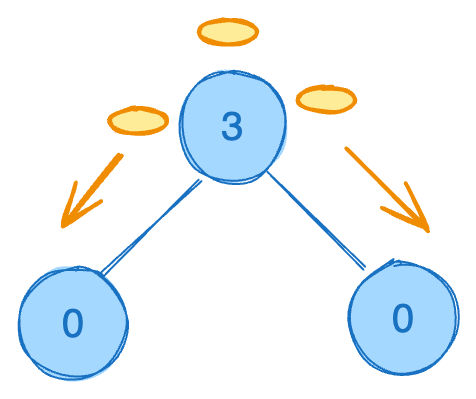
Input: root = [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

1
2
3

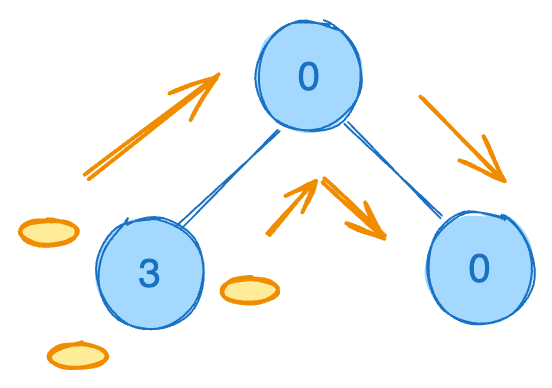
Input: root = [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

Solution

Method 1 - Post-order traversal with global variable

Intuition

We have to distribute the coins from nodes with coins to others. These nodes with coin can be parent or child. If they are parent, we can go downwards and distribute them like we saw in example 1. But if they are child, we have to distribute it to parents and other nodes. In binary tree, it is easy to go from parent to child, but we have to also go from child to parent, and hence we can use post-order traversal. In post-order traversal we process children first, and then parent.

Algorithm

0. Initiate global variable move to 0
1. Base case - if root is null, we return 0 as no coins are required because null node is already balanced
2. Now, we start post-order dfs on left and right children and get coinsLeft and coinsRight which are extra coins available in left and right subtree
3. Now we add coins as sum of coinsLeft and coinsRight
4. Now, we process current node root.
   1. root.val == 0 ⇨ root node cannot contribute, but needs coin from its parent ⇨ coins is reduced by 1, as current node will use one of the coin for itself.
   2. root.val >= 1
      1. root.val == 1 ⇨ root is coin neutral - it cannot contribute but is self-sufficient.
      2. root.val > 1 ⇨ root node can also contribute to other nodes. (If coins was negative, it will contribute some to children in away but if it was positive, it will send it to its parent). This will increase number of coins available at current node by root.val - 1.
   3. So, basically we coins += (root.val - 1)
5. Based on 4, we can calculate move as Math.abs(coins) - where if coins < 0, this node takes the coin, but coin > 0 this node gives it back, but both will cost those many moves, as we are allowed to move only 1 coin at a time.

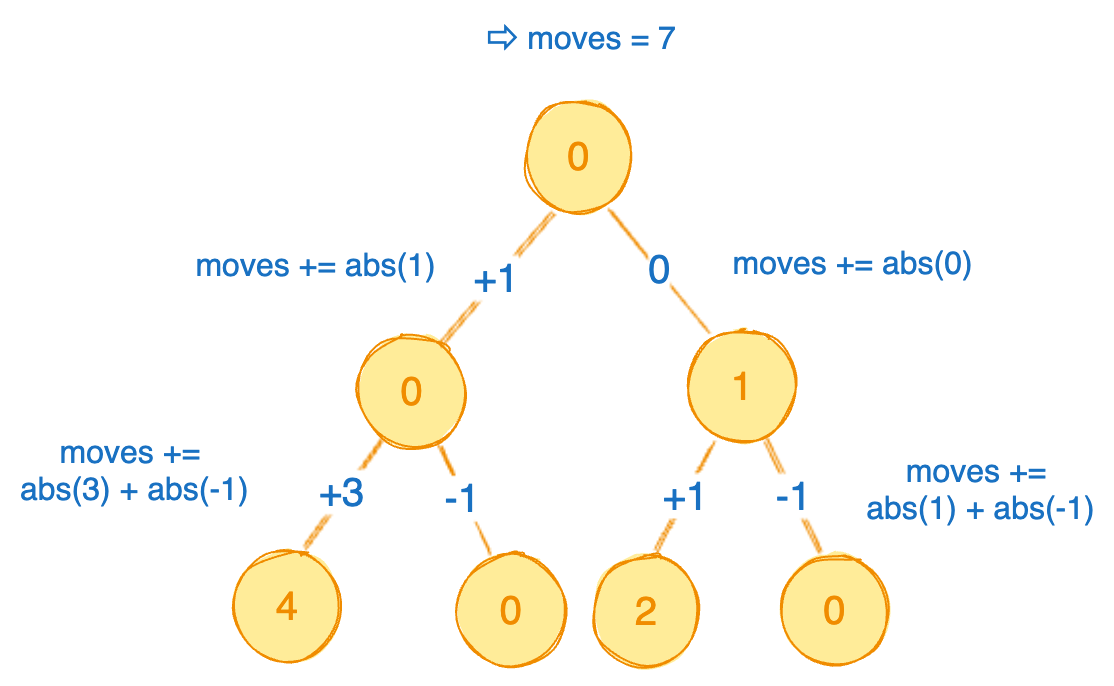
Dry Run

Lets look at coins returned by dfs from different nodes:

Video Explanation

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
	int moves = 0; // our answer
	public int distributeCoins(TreeNode root) {
		helper(root);
		return moves;
	}

	private int helper(TreeNode root) {
		if (root == null) {
			return 0;
		}

		int coinsLeft = helper(root.left);
		int coinsRight = helper(root.right);

		int coins = coinsLeft + coinsRight;

		coins += (root.val - 1);

		moves += Math.abs(coins);

		return coins;
	}
}

Complexity

• ⏰ Time complexity: O(n)
• 🧺 Space complexity: O(h) => O(n) (assuming recursive stack)