Problem

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

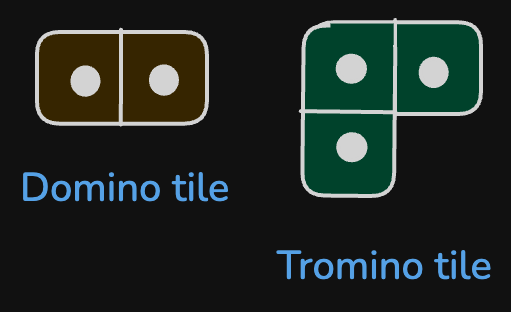
Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 10^9 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Examples

Example 1:

1
2
3

Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

1
2

Input: n = 1
Output: 1

Solution

Method 1 - Naive recursion

We are given a 2 × n grid, and we need to find the number of ways to tile the grid using the following tiles:

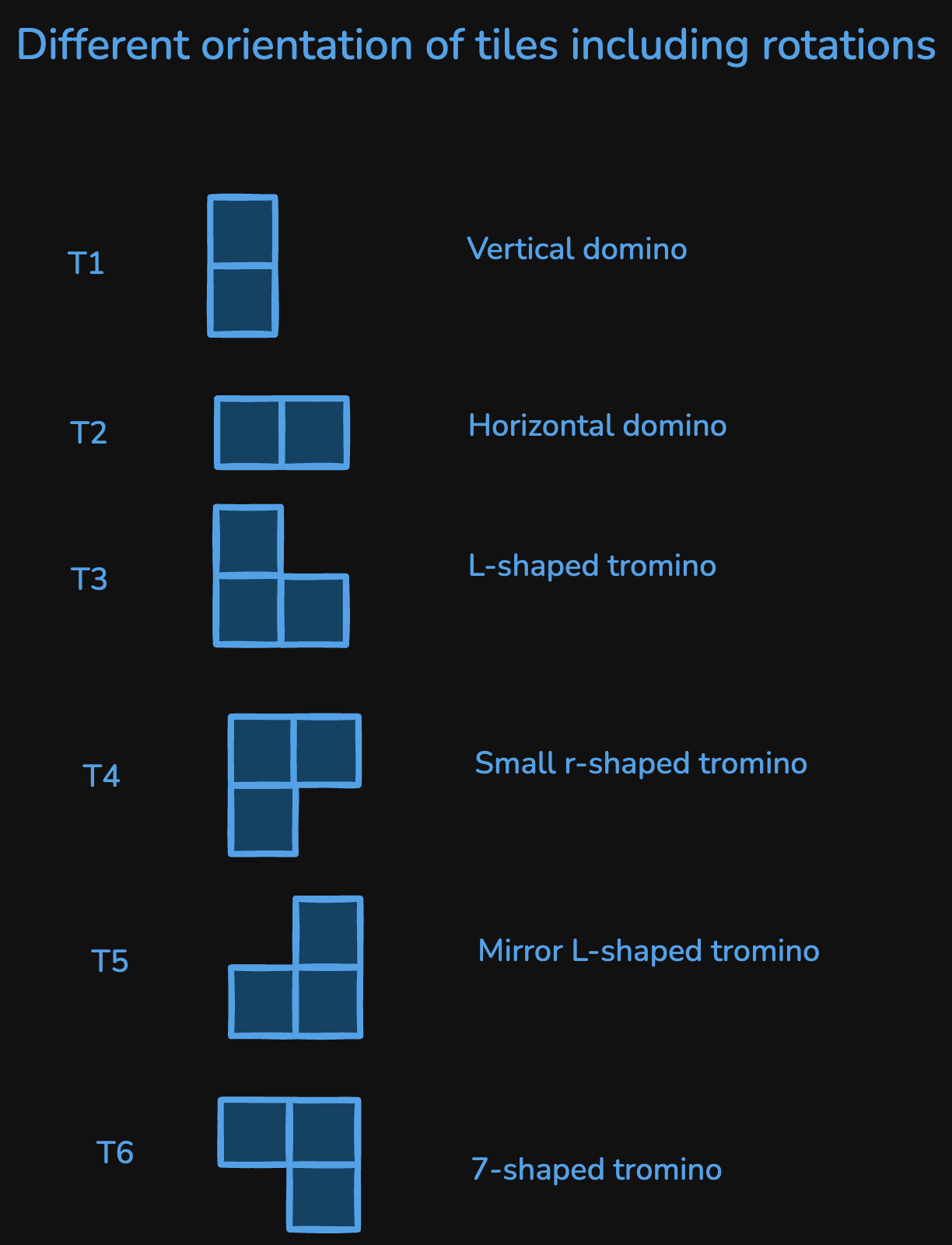
So, in total, we have 6 different types of tiles:

  • T1 and T2 (from dominoes)
  • T3, T4, T5, and T6 (from trominoes)

Let’s see how we can approach this problem using brute-force approach. Since we are only given a 2xn grid, let our current position on the grid be denoted by an index i which denotes that we are currently at ith column of grid.

Filling the rows

To fill in the 2 rows, we need:

  • The parameter n represents the number of columns remaining in the grid that we need to tile.
    • Each tile placement reduces the number of remaining columns based on its dimensions (how much of the grid it covers).
  • and the column state

Column states

Based on that we may have a column state:

  • 0 → gap in row 1 only (▉▉▃)
  • 1 → gap in row 1 only (▉▉▀)
  • 2 → no gaps (▉▉▉)

At each column, we have the choice to choose any form of the above 6 tiles. However, the current choice will be limited by our previous choices.

Column state is 0

This means the top row has a gap at column i, while the bottom row is fully tiled up to column i.

From this configuration, let’s consider the valid tile placement cases:

  1. Case 1: Place an L-shaped tromino (T6) to fill the top-row gap:
    • This tromino extends across two columns (i and i+1).
    • It fills the top-row gap at column i while leaving no gaps in column i+1 (both rows now fully filled).
    • The grid state transitions to colState = 2 (no gaps), which refers to a fully tiled state.
    • Now, 2 columns are properly fixed thanks to this, hence we have n - 2 columns to fill in afterwards
  2. Case 2: Place a horizontal domino to fill the top-row gap at column i:
    • This domino fills the gap in the top row.
    • However, it introduces a gap in the bottom row in the next column (i+1).
    • The grid state transitions to colState = 1, which indicates a bottom-row gap.
    • This time, only 1 column is properly fixed, leaving the remaining n - 1 columns to be tiled.
Column state is 1

When colState == 1, the current configuration of the grid indicates:

  • The bottom row has a gap at column i.
  • The top row is fully tiled up to column i.

At this point, we can place tiles to progress in two valid ways:

  1. Case 1: Place an L-shaped tromino (T4 or mirrored T5) to fill the bottom-row gap

    • This tromino spans two columns (i and i+1).
    • It fills the bottom-row gap at column i while leaving no gaps in column i+1 (both rows now become fully tiled).
    • The grid state transitions to colState = 2, indicating no gaps remain, meaning both rows are fully tiled at this point.
    • Since 2 columns are fully tiled, the recursive function reduces the problem by considering the remaining n - 2 columns.

  2. Case 2: Place a horizontal domino to fill the bottom-row gap

    • This domino spans one column and fills the bottom-row gap at column i, but it introduces a gap in the top row at column i+1.
    • The grid state transitions to colState = 0, indicating a new gap in the top row at the next column.
    • Since 1 column is tiled in this step, the recursive function reduces the problem by considering the remaining n - 1 columns.
Column state is 2

When colState == 2, both rows up to column i are fully tiled (there are no gaps in column i or earlier). From this fully tiled state, we consider all possible ways to progress while tiling the remaining grid.

  1. Case 1: Place a vertical domino (n - 1, 0)

    • A vertical domino spans 1 column (column i), filling the top and bottom rows completely at that column.
    • However, this introduces a gap into the top row of the next column (i + 1).
    • The grid state transitions to colState = 0 (gap introduced in the top row).
    • Since a vertical domino covers 1 column, the recursive function progresses with n - 1 columns remaining.

  2. Case 2: Place a vertical domino (n - 1, 1)

    • A vertical domino spans 1 column (column i), filling the top and bottom rows completely at that column.
    • This introduces a gap into the bottom row of the next column (i + 1).
    • The grid state transitions to colState = 1 (gap introduced in the bottom row).
    • Since a vertical domino covers 1 column, the recursive function progresses with n - 1 columns remaining.

  3. Case 3: Place two horizontal dominoes (n - 1, 2)

    • Two horizontal dominoes span 1 column each, covering both rows at column i.
    • After placing two horizontal dominoes, both rows are fully tiled at this state.
    • The grid state remains colState = 2 (fully tiled).
    • Since two horizontal dominoes are used, the recursive function progresses with n - 1 columns remaining.

  4. Case 4: Place a tromino to cover 2 × 3 (n - 2, 2)

    • A tromino spans 2 columns, completely filling both rows at those columns.
    • This does not introduce any gaps, leaving both rows fully tiled.
    • The grid state remains colState = 2 (fully tiled).
    • Since a tromino spans 2 columns, the recursive function progresses with n - 2 columns remaining.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    private static final int MOD = 1_000_000_007;

    public int numTilings(int n) {
        return numTilingsForFinalStateOf(n, 2);
    }

    public int numTilingsForFinalStateOf(int n, int colState) {
        if (n < 0) return 0;

        // Goal achieved when no columns remain and no gaps exist
        if (n == 0) {
            return colState == 2 ? 1 : 0;
        }

        long ways = 0;
        if (colState == 0) { // Current configuration: ▉▉▀
            ways += numTilingsForFinalStateOf(n - 2, 2); // ▉
            ways += numTilingsForFinalStateOf(n - 1, 1); // ▉▃
        } else if (colState == 1) { // Current configuration: ▉▉▃
            ways += numTilingsForFinalStateOf(n - 2, 2); // ▉
            ways += numTilingsForFinalStateOf(n - 1, 0); // ▉▀
        } else if (colState == 2) { // Current configuration: ▉▉▉
            ways += numTilingsForFinalStateOf(n - 1, 0); // ▉▀
            ways += numTilingsForFinalStateOf(n - 1, 1); // ▉▃
            ways += numTilingsForFinalStateOf(n - 1, 2); // ▉▉
            ways += numTilingsForFinalStateOf(n - 2, 2); // ▉
        }

        return (int) (ways % MOD);
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution:
    MOD = 10**9 + 7

    def numTilings(self, n: int) -> int:
        def num_tilings_for_final_state(n: int, col_state: int) -> int:
            if n < 0:
                return 0
            
            # Goal achieved when no columns remain and no gaps exist
            if n == 0:
                return 1 if col_state == 2 else 0
            
            ways = 0
            if col_state == 0:  # Current configuration: ▉▉▀
                ways += num_tilings_for_final_state(n - 2, 2)  # ▉
                ways += num_tilings_for_final_state(n - 1, 1)  # ▉▃
            elif col_state == 1:  # Current configuration: ▉▉▃
                ways += num_tilings_for_final_state(n - 2, 2)  # ▉
                ways += num_tilings_for_final_state(n - 1, 0)  # ▉▀
            elif col_state == 2:  # Current configuration: ▉▉▉
                ways += num_tilings_for_final_state(n - 1, 0)  # ▉▀
                ways += num_tilings_for_final_state(n - 1, 1)  # ▉▃
                ways += num_tilings_for_final_state(n - 1, 2)  # ▉▉
                ways += num_tilings_for_final_state(n - 2, 2)  # ▉

            return ways % self.MOD

        return num_tilings_for_final_state(n, 2)

Complexity

  • ⏰ Time complexity: O(3^n). The naive approach involves exploring all possible tile combinations at each column n, leading to 3 recursive branches (colState values). The total number of recursive calls grows exponentially, resulting in O(3^n) due to the branching factor.
  • 🧺 Space complexity: O(n). The space complexity arises from the recursion stack depth, which is proportional to the number of columns (n). Without memoisation, only the stack is used, making the space complexity O(n).

Method 2 - Top Down DP

Caching (or memoisation) is critical to avoid redundant calculations for overlapping subproblems. Without caching, similar states (e.g., (n, colState)) are recomputed, leading to inefficiency. Memoisation stores already computed results, reducing the time complexity from exponential to linear.

We use a hash map (in Java) or a dictionary (in Python) to store the results for each state (n, colState):

  • Before performing recursive calls, we check if the result for a given state is already cached in the map/dictionary.
  • If cached, directly return the stored result.
  • Otherwise, calculate the result, store it in the map/dictionary, and return it.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
    private static final int MOD = 1_000_000_007;
    private Map<String, Integer> memo = new HashMap<>(); // For caching results

    public int numTilings(int n) {
        return numTilingsForFinalState(n, 2);
    }

    private int numTilingsForFinalState(int n, int colState) {
        if (n < 0) return 0;
        if (n == 0) return colState == 2 ? 1 : 0; // Base case: fully tiled
        
        String key = n + "|" + colState; // Key for caching based on column state
        if (memo.containsKey(key)) return memo.get(key); // Return cached result if present

        long ways = 0;
        if (colState == 0) {
            ways += numTilingsForFinalState(n - 2, 2);
            ways += numTilingsForFinalState(n - 1, 1);
        } else if (colState == 1) {
            ways += numTilingsForFinalState(n - 2, 2);
            ways += numTilingsForFinalState(n - 1, 0);
        } else if (colState == 2) {
            ways += numTilingsForFinalState(n - 1, 0);
            ways += numTilingsForFinalState(n - 1, 1);
            ways += numTilingsForFinalState(n - 1, 2);
            ways += numTilingsForFinalState(n - 2, 2);
        }

        ways = Math.floorMod(ways, MOD); // Apply modulo constraint
        memo.put(key, (int) ways); // Cache computed result for this state
        return (int) ways;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution:
    MOD = 10**9 + 7
    
    def __init__(self):
        self.memo = {}  # For caching results

    def numTilings(self, n: int) -> int:
        return self.num_tilings_for_final_state(n, 2)

    def num_tilings_for_final_state(self, n: int, col_state: int) -> int:
        if n < 0:
            return 0
        if n == 0:
            return 1 if col_state == 2 else 0  # Base case: fully tiled
        
        key = (n, col_state)  # Key for caching based on column state
        if key in self.memo:  # Return cached result if present
            return self.memo[key]
        
        ways = 0
        if col_state == 0:  # Top-row gap
            ways += self.num_tilings_for_final_state(n - 2, 2)
            ways += self.num_tilings_for_final_state(n - 1, 1)
        elif col_state == 1:  # Bottom-row gap
            ways += self.num_tilings_for_final_state(n - 2, 2)
            ways += self.num_tilings_for_final_state(n - 1, 0)
        elif col_state == 2:  # Fully tiled
            ways += self.num_tilings_for_final_state(n - 1, 0)
            ways += self.num_tilings_for_final_state(n - 1, 1)
            ways += self.num_tilings_for_final_state(n - 1, 2)
            ways += self.num_tilings_for_final_state(n - 2, 2)
        
        self.memo[key] = ways % self.MOD  # Cache computed result for this state
        return ways % self.MOD

Complexity

  • ⏰ Time complexity: O(n)
    • Using memoisation ensures every unique state (n, colState) is calculated only once.
    • For n columns with 3 possible states (colState = 0, 1, 2), the total number of unique states is O(3 * n).
    • Each state is computed in constant time (O(1)), so the overall time complexity is O(n).
  • 🧺 Space complexity: O(n).
    • The memoisation structure stores 3 * n states, requiring O(n) space.
    • The recursion stack depth is at most n, also contributing O(n) space.
    • Total space complexity: O(n).

Method 3 - Bottom up DP

The bottom-up DP approach avoids recursion by iteratively solving subproblems starting from smaller grids. The key idea is to represent the state of each column using three configurations:

  1. Column State Definitions:
    • colState = 0 (▉▉▀): Top row has a gap, bottom row is fully tiled.
    • colState = 1 (▉▉▃): Bottom row has a gap, top row is fully tiled.
    • colState = 2 (▉▉▉): Both rows are fully tiled (no gaps).
  2. Transition Logic:
    • Compute the number of ways to reach each state (colState = 0, 1, 2) for column i based on previous columns (i-1 and i-2).
    • Update the state using predefined transitions that depend on tile placements (domino and tromino tiles).
  3. Base Cases:
    • colState = 2: Only 1 way to tile an empty grid.
    • colState = 0 & colState = 1: Impossible to start with a gap in row 1 or row 2 for n = 1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class Solution {
    public int numTilings(int n) {
        int mod = 1_000_000_007;
        long dp[][] = new long[n + 1][3]; // DP table storing states for n columns

        // Base cases
        dp[0][0] = 1; // Fully tiled empty grid
        dp[0][1] = 1; // Fully tiled empty grid
        dp[0][2] = 1; // Fully tiled empty grid
        dp[1][0] = 0; // Cannot start with a gap for n = 1
        dp[1][1] = 0; // Cannot start with a gap for n = 1
        dp[1][2] = 1; // Fully tiled grid with n = 1

        // Iterate from 2 to n and compute states
        for (int i = 2; i <= n; i++) {
            // Calculate ways to transition to ▉▉▀ (colState = 0)
            dp[i][0] += dp[i - 1][1]; // Transition from bottom-row gap ▉▃
            dp[i][0] += dp[i - 2][2]; // Transition from fully tiled ▉▉▉ and adding ▉▀
            dp[i][0] = Math.floorMod(dp[i][0], mod);

            // Calculate ways to transition to ▉▉▃ (colState = 1)
            dp[i][1] += dp[i - 1][0]; // Transition from top-row gap ▉▀
            dp[i][1] += dp[i - 2][2]; // Transition from fully tiled ▉▉▉ and adding ▉▃
            dp[i][1] = Math.floorMod(dp[i][1], mod);

            // Calculate ways to transition to ▉▉▉ (colState = 2)
            dp[i][2] += dp[i - 1][2]; // Transition from fully tiled ▉▉▉
            dp[i][2] += dp[i - 2][2]; // Transition from fully tiled and adding ▉═▉═
            dp[i][2] += dp[i - 1][0]; // Transition from top-row gap ▉▀ with additional ▉▃
            dp[i][2] += dp[i - 1][1]; // Transition from bottom-row gap ▉▃ with additional ▉▀
            dp[i][2] = Math.floorMod(dp[i][2], mod);
        }

        return (int) dp[n][2]; // Fully tiled state for n columns
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution:
    def numTilings(self, n: int) -> int:
        MOD = 10**9 + 7
        dp = [[0] * 3 for _ in range(n + 1)]  # DP table storing states for n columns

        # Base cases
        dp[0][0] = 1  # Fully tiled empty grid
        dp[0][1] = 1  # Fully tiled empty grid
        dp[0][2] = 1  # Fully tiled empty grid
        dp[1][0] = 0  # Cannot start with a gap for n = 1
        dp[1][1] = 0  # Cannot start with a gap for n = 1
        dp[1][2] = 1  # Fully tiled grid with n = 1

        # Iterate from 2 to n and compute states
        for i in range(2, n + 1):
            # Calculate ways to transition to ▉▉▀ (colState = 0)
            dp[i][0] = (dp[i - 1][1] + dp[i - 2][2]) % MOD  # ▉▃ + ▉▀

            # Calculate ways to transition to ▉▉▃ (colState = 1)
            dp[i][1] = (dp[i - 1][0] + dp[i - 2][2]) % MOD  # ▉▀ + ▉▃

            # Calculate ways to transition to ▉▉▉ (colState = 2)
            dp[i][2] = (dp[i - 1][2] + dp[i - 2][2] + dp[i - 1][0] + dp[i - 1][1]) % MOD  # Fully tiled states
        return dp[n][2]  # Fully tiled state for n columns

Complexity

  • ⏰ Time complexity: O(n).
    • We compute the DP table for n columns and evaluate 3 states (colState = 0, 1, 2) for each column.
    • Each state calculation takes constant time (O(1)).
    • Overall time complexity: O(n).
  • 🧺 Space complexity: O(n)
    • The DP table requires O(n * 3) space since we store results for 3 states for each column.
    • Hence, space complexity is O(n).