Edge-Disjoint Hamiltonian Circuits and the Round Table Seating ProblemShow thinking

Problem

Given a complete graph with N vertices, how many edge-disjoint Hamiltonian circuits exist? (A Hamiltonian circuit is a cycle that visits every vertex exactly once and returns to the starting vertex.)

OR

Suppose there are N people who meet each evening for dinner at a round table. They want to arrange their seating so that every member has different neighbors every evening. For how many days can this arrangement last?

OR

Given a list of N cities and roads connecting them, can a salesman visit each city exactly once and return to the start? (This is the Hamiltonian cycle problem.)

Examples

Example 1

Input:
N = 21

Output:
10

Explanation:
Each evening, the group sits in a new arrangement so that no two people have the same neighbors as any previous evening. The maximum number of such days is (N-1)/2 = 10.

Example 2

Input:
N = 7

Output:
3

Explanation:
For 7 people, there are 3 edge-disjoint Hamiltonian circuits in the complete graph, so the arrangement can last 3 days.

Solution

Method 1 – Backtracking

Intuition

For a general graph (not necessarily complete), we can use backtracking to search for a Hamiltonian circuit. The idea is to try all possible paths starting from a vertex, marking vertices as visited, and backtracking if a dead end is reached. If we return to the starting vertex after visiting all vertices exactly once, we have found a Hamiltonian circuit.

Approach

1. Start from any vertex (commonly vertex 0).
2. Use a recursive function to try to extend the current path by visiting unvisited neighbors.
3. Mark each visited vertex to avoid revisiting.
4. If all vertices are visited and there is an edge back to the start, a Hamiltonian circuit is found.
5. Backtrack if no further progress can be made.

Code

C++

class Solution {
public:
  bool hamiltonianCircuit(vector<vector<int>>& graph) {
    int n = graph.size();
    vector<bool> vis(n, false);
    vector<int> path;
    path.push_back(0);
    vis[0] = true;
    return dfs(graph, 0, path, vis, n);
  }
private:
  bool dfs(vector<vector<int>>& graph, int u, vector<int>& path, vector<bool>& vis, int n) {
    if (path.size() == n) return graph[u][0] == 1;
    for (int v = 0; v < n; ++v) {
      if (!vis[v] && graph[u][v]) {
        vis[v] = true;
        path.push_back(v);
        if (dfs(graph, v, path, vis, n)) return true;
        vis[v] = false;
        path.pop_back();
      }
    }
    return false;
  }
};

Java

class Solution {
  public boolean hamiltonianCircuit(int[][] graph) {
    int n = graph.length;
    boolean[] vis = new boolean[n];
    List<Integer> path = new ArrayList<>();
    path.add(0);
    vis[0] = true;
    return dfs(graph, 0, path, vis, n);
  }
  private boolean dfs(int[][] graph, int u, List<Integer> path, boolean[] vis, int n) {
    if (path.size() == n) return graph[u][0] == 1;
    for (int v = 0; v < n; ++v) {
      if (!vis[v] && graph[u][v] == 1) {
        vis[v] = true;
        path.add(v);
        if (dfs(graph, v, path, vis, n)) return true;
        vis[v] = false;
        path.remove(path.size() - 1);
      }
    }
    return false;
  }
}

Python

class Solution:
  def hamiltonian_circuit(self, graph: list[list[int]]) -> bool:
    n = len(graph)
    vis = [False] * n
    path = [0]
    vis[0] = True
    def dfs(u: int) -> bool:
      if len(path) == n:
        return graph[u][0] == 1
      for v in range(n):
        if not vis[v] and graph[u][v]:
          vis[v] = True
          path.append(v)
          if dfs(v):
            return True
          vis[v] = False
          path.pop()
      return False
    return dfs(0)

Complexity

• ⏰ Time complexity: O(n!), as all possible permutations of vertices may be checked in the worst case.
• 🧺 Space complexity: O(n), for the recursion stack and path/visited arrays.

Method 2 – Combinatorics

Intuition

A Hamiltonian circuit is a closed path in a graph that visits every vertex exactly once and returns to the starting vertex. In a complete graph (where every vertex is connected to every other vertex), it is possible to construct multiple Hamiltonian circuits that do not share any edges—these are called edge-disjoint Hamiltonian circuits.

This property is useful for problems like the seating arrangement, where each person must have different neighbors every day. Each edge-disjoint Hamiltonian circuit corresponds to a unique arrangement.

Approach

1. In a complete graph with N vertices (where N is odd and N > 1), the number of edge-disjoint Hamiltonian circuits is (N-1)/2.
2. Each circuit represents a unique seating arrangement where no two people have the same neighbors as before.
3. This is because each Hamiltonian circuit uses N edges, and the total number of edges in a complete graph is N(N-1)/2.
4. The construction can be visualized by incrementally increasing the "distance" between neighbors in the seating arrangement each day.
5. For even N, such a set of edge-disjoint Hamiltonian circuits does not exist for all edges.

Example Visualization

Suppose N = 7. The following image shows how edge-disjoint Hamiltonian circuits can be constructed by increasing the "distance" between neighbors each day:

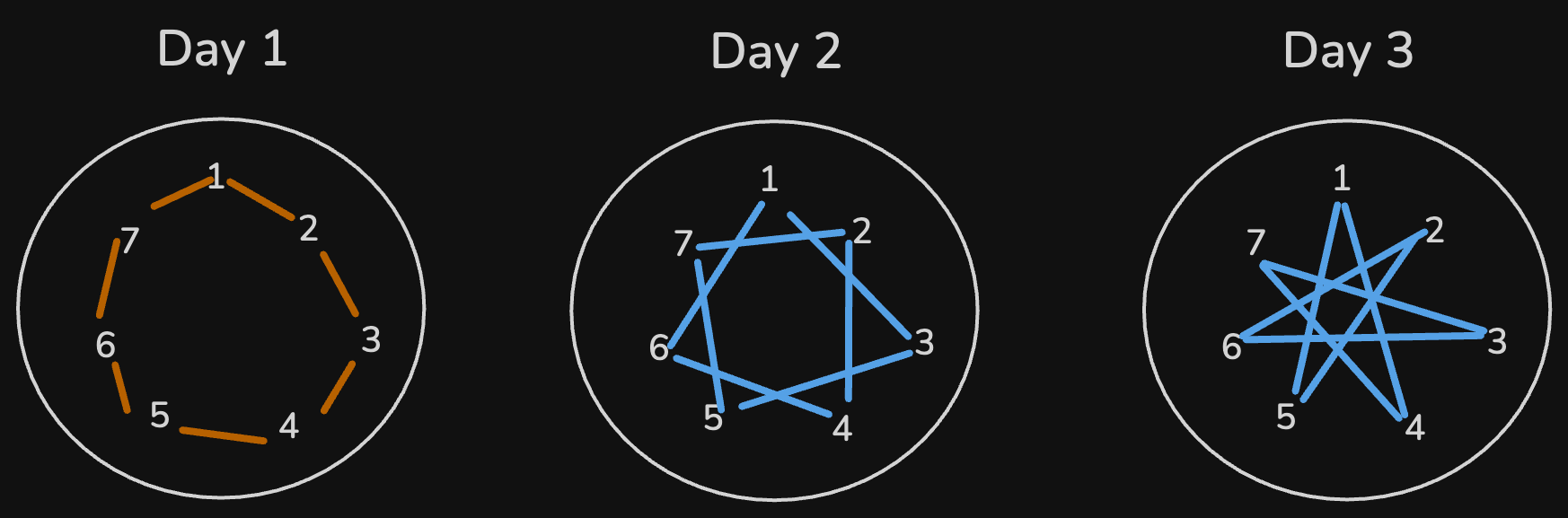
Day 1: Each person sits next to their immediate neighbors. Day 2: Each person sits with neighbors one seat apart from the previous day. Day 3: Each person sits with neighbors two seats apart from the previous day. After (N-1)/2 days, all possible edge-disjoint arrangements are exhausted.

Code

This is a combinatorial result, but you can compute the answer as:

C++

class Solution {
public:
  int maxSeatingArrangements(int n) {
    if (n <= 1 || n % 2 == 0) return 0;
    return (n - 1) / 2;
  }
};

Java

class Solution {
  public int maxSeatingArrangements(int n) {
    if (n <= 1 || n % 2 == 0) return 0;
    return (n - 1) / 2;
  }
}

Python

class Solution:
  def max_seating_arrangements(self, n: int) -> int:
    if n <= 1 or n % 2 == 0:
      return 0
    return (n - 1) // 2

Complexity

• ⏰ Time complexity: O(1), as the answer is computed directly from the formula.
• 🧺 Space complexity: O(1), only a few variables are used.

Additional Notes

• A Hamiltonian circuit in a graph with N vertices has exactly N edges.
• In a complete graph, the number of edge-disjoint Hamiltonian circuits is maximized when N is odd.
• Edge-disjoint means no two circuits share any edge.
• This result is useful for problems involving unique neighbor arrangements, such as seating or round-robin tournaments.