problemmediumalgorithmsleetcode-690leetcode 690leetcode690

Employee Importance

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.

You are given an array of employees employees where:

  • employees[i].id is the ID of the ith employee.
  • employees[i].importance is the importance value of the ith employee.
  • employees[i].subordinates is a list of the IDs of the direct subordinates of the ith employee.

Given an integer id that represents an employee's ID, return thetotal importance value of this employee and all their direct and indirect subordinates.

Examples

Example 1


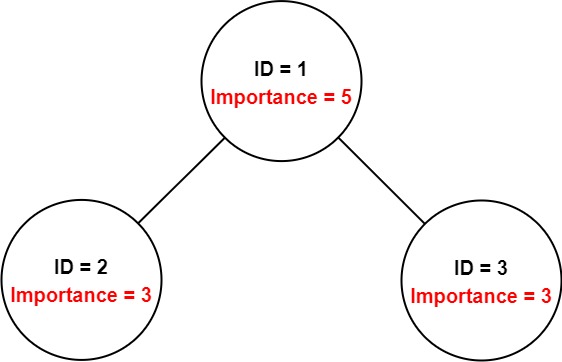
![](https://assets.leetcode.com/uploads/2021/05/31/emp1-tree.jpg)

Input: employees = [[1,5,[2,3]],[2,3,[]],[3,3,[]]], id = 1
Output: 11
Explanation: Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.

Example 2


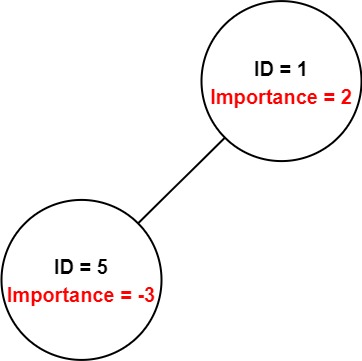
![](https://assets.leetcode.com/uploads/2021/05/31/emp2-tree.jpg)

Input: employees = [[1,2,[5]],[5,-3,[]]], id = 5
Output: -3
Explanation: Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.

Constraints

  • 1 <= employees.length <= 2000
  • 1 <= employees[i].id <= 2000
  • All employees[i].id are unique.
  • -100 <= employees[i].importance <= 100
  • One employee has at most one direct leader and may have several subordinates.
  • The IDs in employees[i].subordinates are valid IDs.

Solution

Method 1 – DFS Traversal (Recursive)

Intuition

The total importance for an employee is the sum of their own importance and the importance of all their direct and indirect subordinates. This is naturally solved by traversing the employee hierarchy recursively.

Approach

  1. Build a map from employee id to employee object for O(1) lookup.
  2. Define a recursive function that, given an employee id, returns the total importance:
    • Add the employee's own importance.
    • For each subordinate, recursively add their total importance.
  3. Start the recursion from the given id.

Code

C++
class Solution {
public:
    int getImportance(vector<Employee*> employees, int id) {
        unordered_map<int, Employee*> mp;
        for (auto e : employees) mp[e->id] = e;
        return dfs(id, mp);
    }
    int dfs(int id, unordered_map<int, Employee*>& mp) {
        int ans = mp[id]->importance;
        for (int sub : mp[id]->subordinates) ans += dfs(sub, mp);
        return ans;
    }
};
Go
type Employee struct {
    Id           int
    Importance   int
    Subordinates []int
}

func getImportance(employees []*Employee, id int) int {
    mp := make(map[int]*Employee)
    for _, e := range employees {
        mp[e.Id] = e
    }
    var dfs func(int) int
    dfs = func(i int) int {
        ans := mp[i].Importance
        for _, sub := range mp[i].Subordinates {
            ans += dfs(sub)
        }
        return ans
    }
    return dfs(id)
}
Java
class Solution {
    public int getImportance(List<Employee> employees, int id) {
        Map<Integer, Employee> mp = new HashMap<>();
        for (Employee e : employees) mp.put(e.id, e);
        return dfs(id, mp);
    }
    private int dfs(int id, Map<Integer, Employee> mp) {
        Employee e = mp.get(id);
        int ans = e.importance;
        for (int sub : e.subordinates) ans += dfs(sub, mp);
        return ans;
    }
}
Kotlin
data class Employee(
    val id: Int,
    val importance: Int,
    val subordinates: List<Int>
)

class Solution {
    fun getImportance(employees: List<Employee>, id: Int): Int {
        val mp = employees.associateBy { it.id }
        fun dfs(i: Int): Int {
            val e = mp[i]!!
            var ans = e.importance
            for (sub in e.subordinates) ans += dfs(sub)
            return ans
        }
        return dfs(id)
    }
}
Python
class Employee:
    def __init__(self, id: int, importance: int, subordinates: list[int]):
        self.id = id
        self.importance = importance
        self.subordinates = subordinates

class Solution:
    def getImportance(self, employees: list[Employee], id: int) -> int:
        mp = {e.id: e for e in employees}
        def dfs(i: int) -> int:
            e = mp[i]
            ans = e.importance
            for sub in e.subordinates:
                ans += dfs(sub)
            return ans
        return dfs(id)
Rust
use std::collections::HashMap;

impl Solution {
    pub fn get_importance(employees: Vec<Employee>, id: i32) -> i32 {
        let mp: HashMap<i32, &Employee> = employees.iter().map(|e| (e.id, e)).collect();
        fn dfs(i: i32, mp: &HashMap<i32, &Employee>) -> i32 {
            let e = mp[&i];
            let mut ans = e.importance;
            for &sub in &e.subordinates {
                ans += dfs(sub, mp);
            }
            ans
        }
        dfs(id, &mp)
    }
}
TypeScript
class Employee {
    id: number;
    importance: number;
    subordinates: number[];
    constructor(id: number, importance: number, subordinates: number[]) {
        this.id = id;
        this.importance = importance;
        this.subordinates = subordinates;
    }
}

class Solution {
    getImportance(employees: Employee[], id: number): number {
        const mp = new Map<number, Employee>();
        for (const e of employees) mp.set(e.id, e);
        function dfs(i: number): number {
            const e = mp.get(i)!;
            let ans = e.importance;
            for (const sub of e.subordinates) ans += dfs(sub);
            return ans;
        }
        return dfs(id);
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of employees. Each employee is visited once.
  • 🧺 Space complexity: O(n), for the map and recursion stack.

Comments