problemmediumalgorithmsleetcode-1256leetcode 1256leetcode1256

Encode Number

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given a non-negative integer num, Return its encoding string.

The encoding is done by converting the integer to a string using a secret function that you should deduce from the following table:

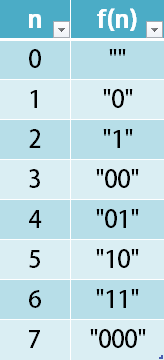
Examples

Example 1:

Input: num = 23
Output: "1000"

Example 2:

Input: num = 107
Output: "101100"

Constraints:

  • 0 <= num <= 10^9

Solution

Method 1 – Binary Representation Minus One

Intuition

The encoding is the binary representation of num + 1, but with the leading '1' removed. This is because the encoding table matches the binary numbers from 1 upwards, skipping the leading bit.

Approach

  1. If num is 0, return an empty string.
  2. Convert num + 1 to its binary representation.
  3. Remove the leading '1' from the binary string.
  4. Return the result.

Code

C++
class Solution {
public:
    string encode(int num) {
        if (num == 0) return "";
        string ans;
        num++;
        while (num > 1) {
            ans = char('0' + (num & 1)) + ans;
            num >>= 1;
        }
        return ans;
    }
};
Go
func encode(num int) string {
    if num == 0 {
        return ""
    }
    num++
    ans := ""
    for num > 1 {
        ans = string('0'+(num&1)) + ans
        num >>= 1
    }
    return ans
}
Java
class Solution {
    public String encode(int num) {
        if (num == 0) return "";
        StringBuilder ans = new StringBuilder();
        num++;
        while (num > 1) {
            ans.insert(0, num & 1);
            num >>= 1;
        }
        return ans.toString();
    }
}
Kotlin
class Solution {
    fun encode(num: Int): String {
        if (num == 0) return ""
        var n = num + 1
        val ans = StringBuilder()
        while (n > 1) {
            ans.insert(0, n and 1)
            n = n shr 1
        }
        return ans.toString()
    }
}
Python
class Solution:
    def encode(self, num: int) -> str:
        if num == 0:
            return ""
        b = bin(num + 1)[3:]
        return b
Rust
impl Solution {
    pub fn encode(num: i32) -> String {
        if num == 0 {
            return String::new();
        }
        let mut n = (num + 1) as u32;
        let mut ans = String::new();
        while n > 1 {
            ans.insert(0, char::from(b'0' + (n & 1) as u8));
            n >>= 1;
        }
        ans
    }
}
TypeScript
class Solution {
    encode(num: number): string {
        if (num === 0) return "";
        let n = num + 1;
        let ans = "";
        while (n > 1) {
            ans = (n & 1) + ans;
            n >>= 1;
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(log n), since we process each bit of the number.
  • 🧺 Space complexity: O(log n), for the output string.

Comments