Equal Sum Grid Partition I
MediumUpdated: Aug 2, 2025
Practice on:
Problem
You are given an m x n matrix grid of positive integers. Your task is to determine if it is possible to make either one horizontal or one vertical cut on the grid such that:
- Each of the two resulting sections formed by the cut is non-empty.
- The sum of the elements in both sections is equal.
Return true if such a partition exists; otherwise return false.
Examples
Example 1

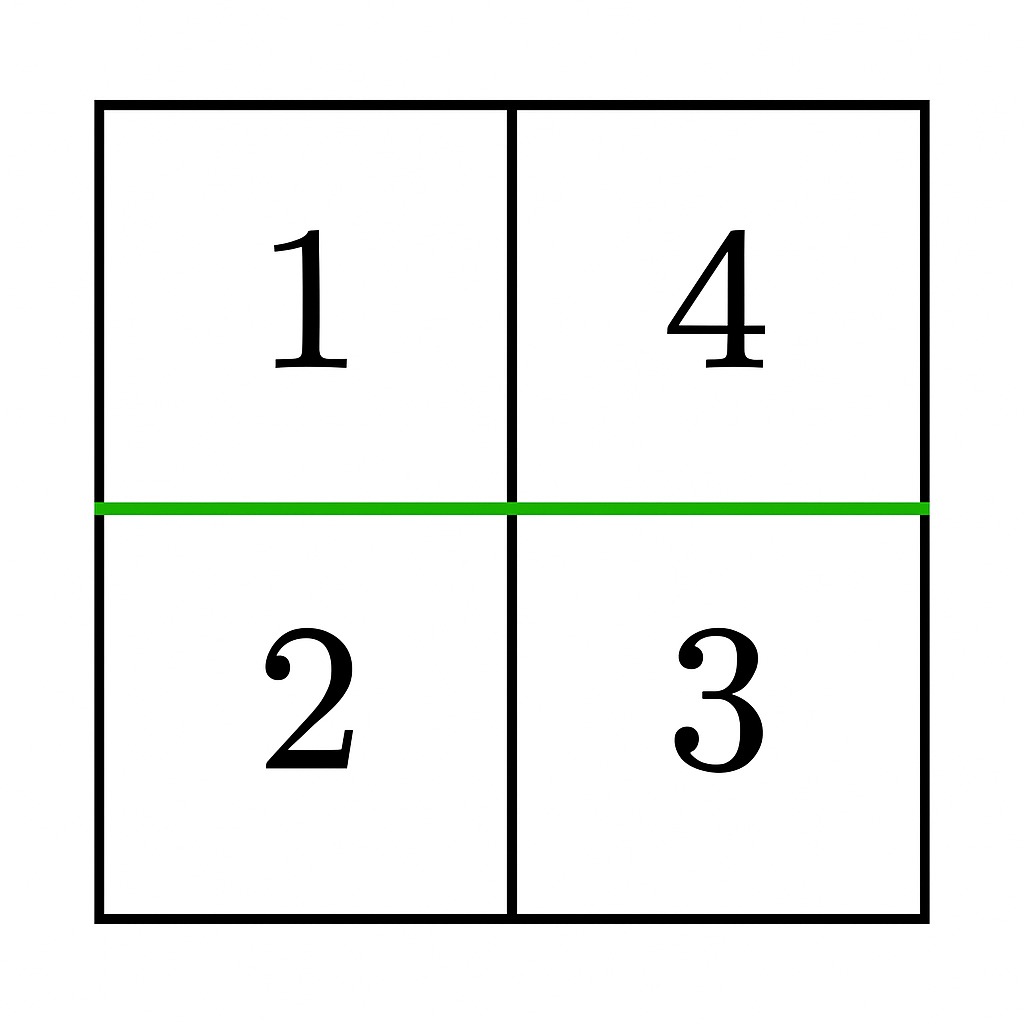
\Huge
\begin{array}{|c|c|}
\hline
1 & 4 \\\\
\hline
2 & 3 \\\\
\hline
\end{array}$$
```d
Input: grid = [[1,4],[2,3]]
Output: true
Explanation:
A horizontal cut between row 0 and row 1 results in two non-empty sections,
each with a sum of 5. Thus, the answer is `true`.
```
#### Example 2
```d
Input: grid = [[1,3],[2,4]]
Output: false
Explanation:
No horizontal or vertical cut results in two non-empty sections with equal
sums. Thus, the answer is `false`.
```
### Constraints
* `1 <= m == grid.length <= 10^5`
* `1 <= n == grid[i].length <= 10^5`
* `2 <= m * n <= 10^5`
* `1 <= grid[i][j] <= 10^5`
## Solution
### Method 1 – Prefix Sum and Cut Check
#### Intuition
If we want to split the grid into two non-empty parts with equal sums using a single horizontal or vertical cut, we can precompute the total sum and check for each possible cut if the sum of one part equals half the total sum.
#### Approach
1. Compute the total sum of all elements in the grid.
2. For each possible horizontal cut (between row i and i+1), compute the sum of the top part using prefix sums. If it equals half the total, return true.
3. For each possible vertical cut (between column j and j+1), compute the sum of the left part using prefix sums. If it equals half the total, return true.
4. If no such cut exists, return false.
#### Code
{{< code_tabs >}}
##### C++
```cpp
class Solution {
public:
bool isPossibleToCutGrid(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
long long total = 0;
for (auto& row : grid) for (int x : row) total += x;
long long row_sum = 0;
for (int i = 0; i < m - 1; ++i) {
for (int x : grid[i]) row_sum += x;
if (row_sum * 2 == total) return true;
}
for (int j = 0; j < n - 1; ++j) {
long long col_sum = 0;
for (int i = 0; i < m; ++i) col_sum += grid[i][j];
if (col_sum * 2 == total) return true;
}
return false;
}
};
```
##### Java
```java
class Solution {
public boolean isPossibleToCutGrid(int[][] grid) {
int m = grid.length, n = grid[0].length;
long total = 0;
for (int[] row : grid) for (int x : row) total += x;
long rowSum = 0;
for (int i = 0; i < m - 1; ++i) {
for (int x : grid[i]) rowSum += x;
if (rowSum * 2 == total) return true;
}
for (int j = 0; j < n - 1; ++j) {
long colSum = 0;
for (int i = 0; i < m; ++i) colSum += grid[i][j];
if (colSum * 2 == total) return true;
}
return false;
}
}
```
##### Python
```python
class Solution:
def isPossibleToCutGrid(self, grid: list[list[int]]) -> bool:
m, n = len(grid), len(grid[0])
total = sum(sum(row) for row in grid)
row_sum = 0
for i in range(m - 1):
row_sum += sum(grid[i])
if row_sum * 2 == total:
return True
for j in range(n - 1):
col_sum = 0
for i in range(m):
col_sum += grid[i][j]
if col_sum * 2 == total:
return True
return False
```
{{< /code_tabs >}}
#### Complexity
- ⏰ Time complexity: `O(mn)`, since we may sum all elements for each possible cut.
- 🧺 Space complexity: `O(1)`, only a few variables for sums.