problemmediumalgorithmsleetcode-663leetcode 663leetcode663

Equal Tree Partition

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given the root of a binary tree, return true if you can partition the tree into two trees with equal sums of values after removing exactly one edge on the original tree.

Examples

Example 1:

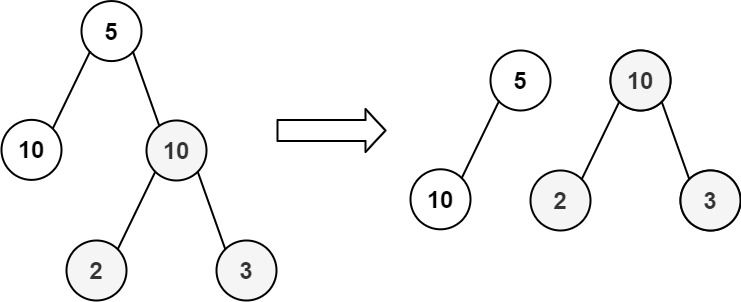
Input: root = [5,10,10,null,null,2,3]
Output: true

Example 2:

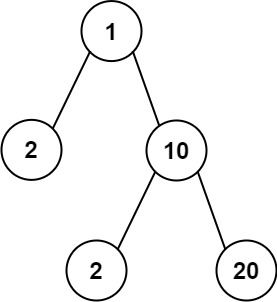
Input: root = [1,2,10,null,null,2,20]
Output: false
Explanation: You cannot split the tree into two trees with equal sums after removing exactly one edge on the tree.

Constraints:

  • The number of nodes in the tree is in the range [1, 10^4].
  • -10^5 <= Node.val <= 10^5

Solution

Method 1 – DFS and Subtree Sum Set

Intuition

If we remove an edge, the tree splits into two subtrees. If the sum of one subtree is exactly half the total sum, the other subtree will also have the same sum. We can use DFS to compute all subtree sums and check if half the total sum exists among them (excluding the whole tree sum itself).

Approach

  1. Compute the total sum of the tree using DFS.
  2. Traverse the tree again with DFS, recording all subtree sums in a set.
  3. If the total sum is even and half the total sum exists in the set (excluding the whole tree), return true.
  4. Otherwise, return false.

Code

C++
class Solution {
public:
    bool checkEqualTree(TreeNode* root) {
        unordered_set<int> sums;
        int total = treeSum(root, sums);
        sums.erase(total);
        return total % 2 == 0 && sums.count(total / 2);
    }
    int treeSum(TreeNode* node, unordered_set<int>& sums) {
        if (!node) return 0;
        int s = node->val + treeSum(node->left, sums) + treeSum(node->right, sums);
        sums.insert(s);
        return s;
    }
};
Java
class Solution {
    public boolean checkEqualTree(TreeNode root) {
        Set<Integer> sums = new HashSet<>();
        int total = treeSum(root, sums);
        sums.remove(total);
        return total % 2 == 0 && sums.contains(total / 2);
    }
    private int treeSum(TreeNode node, Set<Integer> sums) {
        if (node == null) return 0;
        int s = node.val + treeSum(node.left, sums) + treeSum(node.right, sums);
        sums.add(s);
        return s;
    }
}
Python
class Solution:
    def checkEqualTree(self, root: 'TreeNode') -> bool:
        sums = set()
        def dfs(node):
            if not node:
                return 0
            s = node.val + dfs(node.left) + dfs(node.right)
            sums.add(s)
            return s
        total = dfs(root)
        sums.discard(total)
        return total % 2 == 0 and (total // 2) in sums

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nodes (each node is visited once).
  • 🧺 Space complexity: O(n), for storing subtree sums.

Comments