Erect the Fence
HardUpdated: Aug 2, 2025
Practice on:
Problem
You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.
Fence the entire garden using the minimum length of rope, as it is expensive. The garden is well-fenced only if all the trees are enclosed.
Return the coordinates of trees that are exactly located on the fence perimeter. You may return the answer in any order.
Examples
Example 1
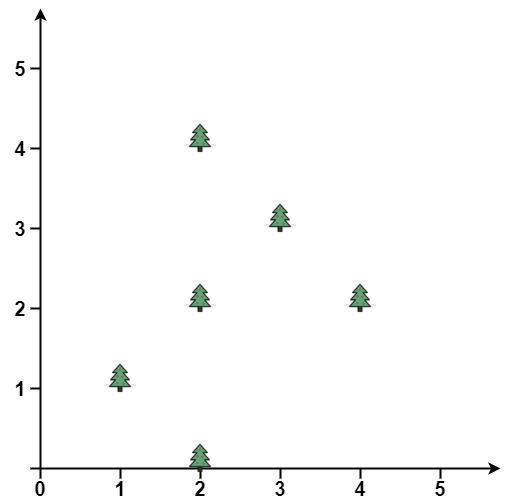
Input: trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[4,2],[3,3],[2,4]]
Explanation: All the trees will be on the perimeter of the fence except the tree at [2, 2], which will be inside the fence.
Example 2
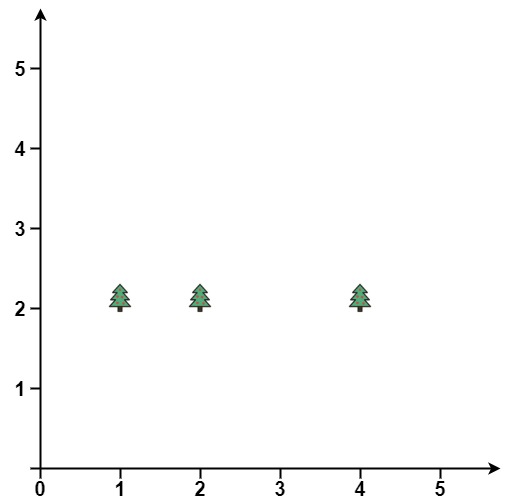
Input: trees = [[1,2],[2,2],[4,2]]
Output: [[4,2],[2,2],[1,2]]
Explanation: The fence forms a line that passes through all the trees.
Constraints
1 <= trees.length <= 3000trees[i].length == 20 <= xi, yi <= 100- All the given positions are unique.
Solution
Method 1 – Monotone Chain Convex Hull
Intuition
The minimum rope length enclosing all trees is the convex hull of the points. The trees on the hull are exactly those on the fence. The Monotone Chain algorithm efficiently finds the convex hull in O(n log n) time and handles collinear points (which must be included on the hull).
Approach
- Sort the points by x, then y.
- Build the lower and upper hulls:
- For each point, while the last two points and the current point make a right turn, pop the last point.
- Add the current point.
- Concatenate lower and upper hulls, removing duplicates.
- Return the hull points.
Code
C++
class Solution {
public:
vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
sort(trees.begin(), trees.end());
vector<vector<int>> hull;
auto cross = [](const vector<int>& o, const vector<int>& a, const vector<int>& b) {
return (a[0] - o[0]) * (b[1] - o[1]) - (a[1] - o[1]) * (b[0] - o[0]);
};
for (int i = 0; i < trees.size(); ++i) {
while (hull.size() >= 2 && cross(hull[hull.size()-2], hull.back(), trees[i]) < 0)
hull.pop_back();
hull.push_back(trees[i]);
}
int t = hull.size() + 1;
for (int i = trees.size() - 2; i >= 0; --i) {
while (hull.size() >= t && cross(hull[hull.size()-2], hull.back(), trees[i]) < 0)
hull.pop_back();
hull.push_back(trees[i]);
}
hull.pop_back();
sort(hull.begin(), hull.end());
hull.erase(unique(hull.begin(), hull.end()), hull.end());
return hull;
}
};
Go
import "sort"
func outerTrees(trees [][]int) [][]int {
sort.Slice(trees, func(i, j int) bool {
if trees[i][0] == trees[j][0] {
return trees[i][1] < trees[j][1]
}
return trees[i][0] < trees[j][0]
})
cross := func(o, a, b []int) int {
return (a[0]-o[0])*(b[1]-o[1]) - (a[1]-o[1])*(b[0]-o[0])
}
hull := [][]int{}
for _, p := range trees {
for len(hull) >= 2 && cross(hull[len(hull)-2], hull[len(hull)-1], p) < 0 {
hull = hull[:len(hull)-1]
}
hull = append(hull, p)
}
t := len(hull) + 1
for i := len(trees) - 2; i >= 0; i-- {
p := trees[i]
for len(hull) >= t && cross(hull[len(hull)-2], hull[len(hull)-1], p) < 0 {
hull = hull[:len(hull)-1]
}
hull = append(hull, p)
}
hull = hull[:len(hull)-1]
uniq := map[[2]int]struct{}{}
res := [][]int{}
for _, p := range hull {
key := [2]int{p[0], p[1]}
if _, ok := uniq[key]; !ok {
uniq[key] = struct{}{}
res = append(res, p)
}
}
return res
}
Java
class Solution {
public int[][] outerTrees(int[][] trees) {
Arrays.sort(trees, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
List<int[]> hull = new ArrayList<>();
for (int[] p : trees) {
while (hull.size() >= 2 && cross(hull.get(hull.size()-2), hull.get(hull.size()-1), p) < 0)
hull.remove(hull.size()-1);
hull.add(p);
}
int t = hull.size() + 1;
for (int i = trees.length - 2; i >= 0; i--) {
int[] p = trees[i];
while (hull.size() >= t && cross(hull.get(hull.size()-2), hull.get(hull.size()-1), p) < 0)
hull.remove(hull.size()-1);
hull.add(p);
}
hull.remove(hull.size()-1);
Set<String> seen = new HashSet<>();
List<int[]> res = new ArrayList<>();
for (int[] p : hull) {
String key = p[0] + "," + p[1];
if (seen.add(key)) res.add(p);
}
return res.toArray(new int[0][]);
}
private int cross(int[] o, int[] a, int[] b) {
return (a[0]-o[0])*(b[1]-o[1]) - (a[1]-o[1])*(b[0]-o[0]);
}
}
Kotlin
class Solution {
fun outerTrees(trees: Array<IntArray>): Array<IntArray> {
trees.sortWith(compareBy({ it[0] }, { it[1] }))
val hull = mutableListOf<IntArray>()
fun cross(o: IntArray, a: IntArray, b: IntArray) = (a[0]-o[0])*(b[1]-o[1]) - (a[1]-o[1])*(b[0]-o[0])
for (p in trees) {
while (hull.size >= 2 && cross(hull[hull.size-2], hull.last(), p) < 0) hull.removeAt(hull.size-1)
hull.add(p)
}
val t = hull.size + 1
for (i in trees.size-2 downTo 0) {
val p = trees[i]
while (hull.size >= t && cross(hull[hull.size-2], hull.last(), p) < 0) hull.removeAt(hull.size-1)
hull.add(p)
}
hull.removeAt(hull.size-1)
return hull.distinctBy { it.toList() }.toTypedArray()
}
}
Python
class Solution:
def outerTrees(self, trees: list[list[int]]) -> list[list[int]]:
trees.sort()
def cross(o, a, b):
return (a[0]-o[0])*(b[1]-o[1]) - (a[1]-o[1])*(b[0]-o[0])
hull = []
for p in trees:
while len(hull) >= 2 and cross(hull[-2], hull[-1], p) < 0:
hull.pop()
hull.append(p)
t = len(hull) + 1
for p in reversed(trees[:-1]):
while len(hull) >= t and cross(hull[-2], hull[-1], p) < 0:
hull.pop()
hull.append(p)
hull.pop()
res = []
seen = set()
for p in hull:
key = tuple(p)
if key not in seen:
seen.add(key)
res.append(p)
return res
Rust
impl Solution {
pub fn outer_trees(mut trees: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
trees.sort();
let cross = |o: &[i32], a: &[i32], b: &[i32]| (a[0]-o[0])*(b[1]-o[1]) - (a[1]-o[1])*(b[0]-o[0]);
let mut hull = vec![];
for p in &trees {
while hull.len() >= 2 && cross(&hull[hull.len()-2], &hull[hull.len()-1], p) < 0 {
hull.pop();
}
hull.push(p.clone());
}
let t = hull.len() + 1;
for p in trees.iter().rev().skip(1) {
while hull.len() >= t && cross(&hull[hull.len()-2], &hull[hull.len()-1], p) < 0 {
hull.pop();
}
hull.push(p.clone());
}
hull.pop();
hull.sort();
hull.dedup();
hull
}
}
TypeScript
class Solution {
outerTrees(trees: number[][]): number[][] {
trees.sort((a, b) => a[0] - b[0] || a[1] - b[1]);
const cross = (o: number[], a: number[], b: number[]) => (a[0]-o[0])*(b[1]-o[1]) - (a[1]-o[1])*(b[0]-o[0]);
const hull: number[][] = [];
for (const p of trees) {
while (hull.length >= 2 && cross(hull[hull.length-2], hull[hull.length-1], p) < 0) hull.pop();
hull.push(p);
}
const t = hull.length + 1;
for (let i = trees.length - 2; i >= 0; i--) {
const p = trees[i];
while (hull.length >= t && cross(hull[hull.length-2], hull[hull.length-1], p) < 0) hull.pop();
hull.push(p);
}
hull.pop();
const seen = new Set<string>();
const res: number[][] = [];
for (const p of hull) {
const key = p.join(",");
if (!seen.has(key)) {
seen.add(key);
res.push(p);
}
}
return res;
}
}
Complexity
- ⏰ Time complexity:
O(n log n), for sorting and hull construction. - 🧺 Space complexity:
O(n), for the hull.