problemhardalgorithmsleetcode-1924leetcode 1924leetcode1924

Erect the Fence II

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a 2D integer array trees where trees[i] = [xi, yi] represents the location of the ith tree in the garden.

You are asked to fence the entire garden using the minimum length of rope possible. The garden is well-fenced only if all the trees are enclosed and the rope used forms a perfect circle. A tree is considered enclosed if it is inside or on the border of the circle.

More formally, you must form a circle using the rope with a center (x, y) and radius r where all trees lie inside or on the circle and r is minimum.

Return the center and radius of the circle as a length 3 array[x, y, r]. Answers within 10-5 of the actual answer will be accepted.

Examples

Example 1:

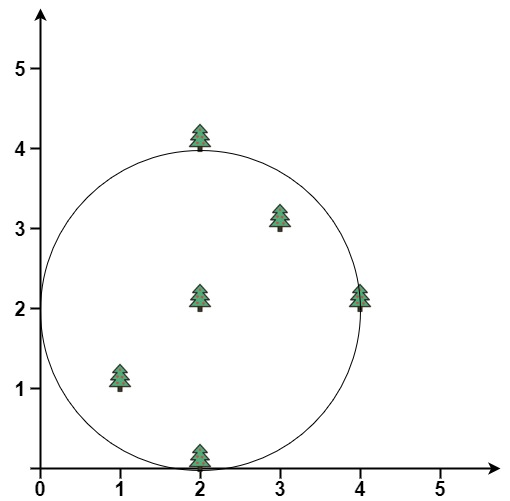**![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1900-1999/1924.Erect%20the%20Fence%20II/images/trees1.png)**
Input: trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [2.00000,2.00000,2.00000]
Explanation: The fence will have center = (2, 2) and radius = 2

Example 2:

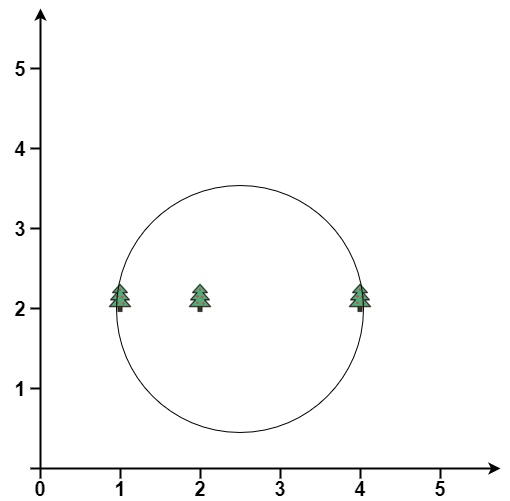**![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1900-1999/1924.Erect%20the%20Fence%20II/images/trees2.png)**
Input: trees = [[1,2],[2,2],[4,2]]
Output: [2.50000,2.00000,1.50000]
Explanation: The fence will have center = (2.5, 2) and radius = 1.5

Constraints:

  • 1 <= trees.length <= 3000
  • trees[i].length == 2
  • 0 <= xi, yi <= 3000

Solution

Method 1 – Welzl's Algorithm (Smallest Enclosing Circle)

Intuition

The minimum rope length that forms a perfect circle enclosing all trees is the smallest enclosing circle (also called the minimum enclosing circle). Welzl's algorithm is a randomized, recursive algorithm that efficiently finds this circle in expected linear time.

Approach

  1. Shuffle the points randomly to ensure average-case performance.
  2. Use Welzl's recursive algorithm:
    • If no points or 3 boundary points, compute the circle directly.
    • Otherwise, remove a point and recursively find the circle for the rest.
    • If the removed point is inside the circle, return the circle.
    • If not, add the point to the boundary and recurse.
  3. For 0, 1, 2, or 3 boundary points, compute the circle directly:
    • 0: return invalid.
    • 1: center is the point, radius 0.
    • 2: center is midpoint, radius is half the distance.
    • 3: compute the unique circle passing through all three points.
  4. Return the center and radius.

Code

Python
import random, math
class Solution:
    def minEnclosingCircle(self, trees: list[list[int]]) -> list[float]:
        def dist(a, b):
            return math.hypot(a[0]-b[0], a[1]-b[1])
        def is_in_circle(p, c):
            return dist(p, c[:2]) <= c[2] + 1e-10
        def circle2(a, b):
            cx = (a[0] + b[0]) / 2
            cy = (a[1] + b[1]) / 2
            r = dist(a, b) / 2
            return [cx, cy, r]
        def circle3(a, b, c):
            A = b[0] - a[0]
            B = b[1] - a[1]
            C = c[0] - a[0]
            D = c[1] - a[1]
            E = A*(a[0]+b[0]) + B*(a[1]+b[1])
            F = C*(a[0]+c[0]) + D*(a[1]+c[1])
            G = 2*(A*(c[1]-b[1]) - B*(c[0]-b[0]))
            if abs(G) < 1e-10:
                return [0,0,float('inf')]
            cx = (D*E - B*F) / G
            cy = (A*F - C*E) / G
            r = dist([cx, cy], a)
            return [cx, cy, r]
        def mec(points, boundary):
            if not points or len(boundary) == 3:
                if len(boundary) == 0:
                    return [0,0,0]
                if len(boundary) == 1:
                    return [boundary[0][0], boundary[0][1], 0]
                if len(boundary) == 2:
                    return circle2(boundary[0], boundary[1])
                return circle3(boundary[0], boundary[1], boundary[2])
            p = points.pop()
            c = mec(points, boundary)
            if is_in_circle(p, c):
                points.append(p)
                return c
            res = mec(points, boundary + [p])
            points.append(p)
            return res
        pts = [tuple(p) for p in trees]
        random.shuffle(pts)
        c = mec(pts[:], [])
        return [float(c[0]), float(c[1]), float(c[2])]

Complexity

  • ⏰ Time complexity: O(n) expected, due to randomization and recursion.
  • 🧺 Space complexity: O(n) for recursion and storage.

Comments