problemhardalgorithmsleetcode-2258leetcode 2258leetcode2258

Escape the Spreading Fire

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a 0-indexed 2D integer array grid of size m x n which represents a field. Each cell has one of three values:

  • 0 represents grass,
  • 1 represents fire,
  • 2 represents a wall that you and fire cannot pass through.

You are situated in the top-left cell, (0, 0), and you want to travel to the safehouse at the bottom-right cell, (m - 1, n - 1). Every minute, you may move to an adjacent grass cell. After your move, every fire cell will spread to all adjacent cells that are not walls.

Return themaximum number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse. If this is impossible, return -1. If you can always reach the safehouse regardless of the minutes stayed, return 109.

Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.

A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).

Examples

Example 1


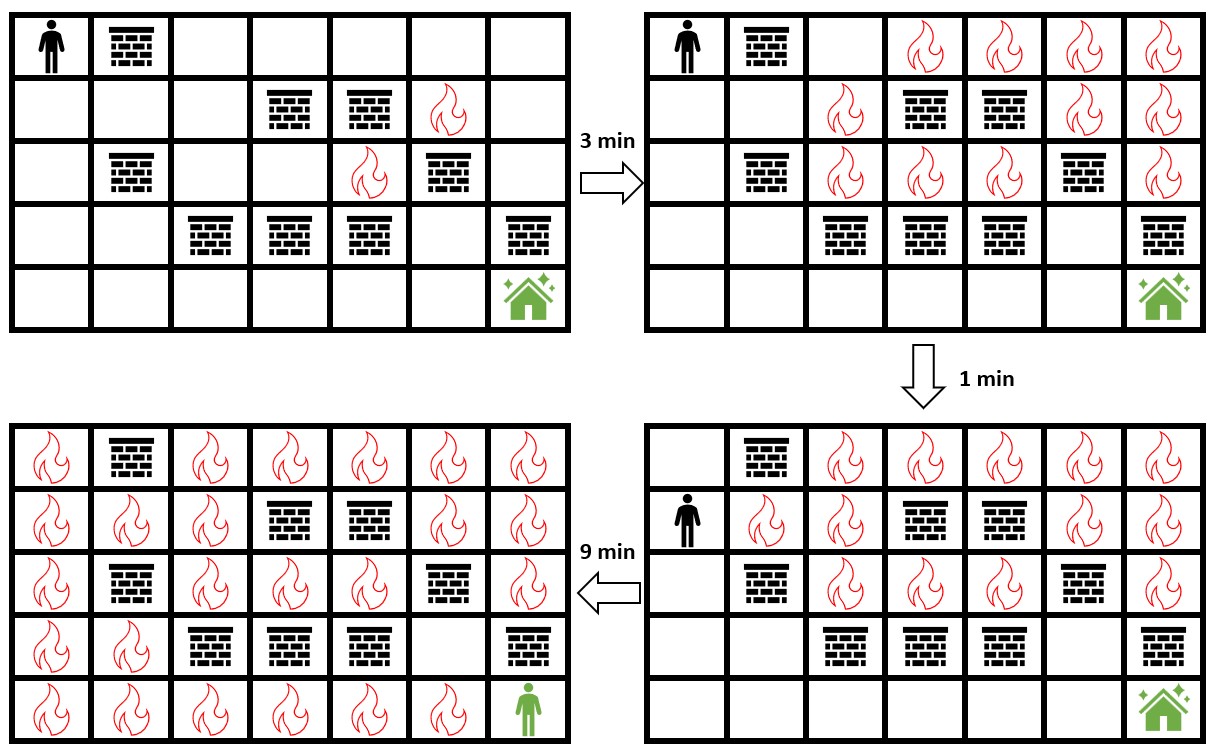
![](https://assets.leetcode.com/uploads/2022/03/10/ex1new.jpg)

Input: grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
Output: 3
Explanation: The figure above shows the scenario where you stay in the initial position for 3 minutes.
You will still be able to safely reach the safehouse.
Staying for more than 3 minutes will not allow you to safely reach the safehouse.

Example 2


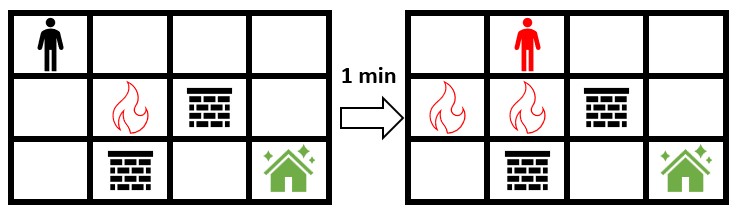
![](https://assets.leetcode.com/uploads/2022/03/10/ex2new2.jpg)

Input: grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
Output: -1
Explanation: The figure above shows the scenario where you immediately move towards the safehouse.
Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse.
Thus, -1 is returned.

Example 3


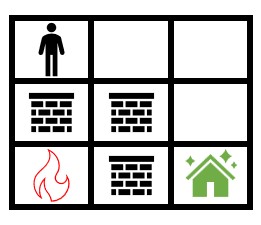
![](https://assets.leetcode.com/uploads/2022/03/10/ex3new.jpg)

Input: grid = [[0,0,0],[2,2,0],[1,2,0]]
Output: 1000000000
Explanation: The figure above shows the initial grid.
Notice that the fire is contained by walls and you will always be able to safely reach the safehouse.
Thus, 109 is returned.

Constraints

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 300
  • 4 <= m * n <= 2 * 10^4
  • grid[i][j] is either 0, 1, or 2.
  • grid[0][0] == grid[m - 1][n - 1] == 0

Solution

Method 1 – Binary Search and Multi-Source BFS

Intuition

The fire spreads every minute, and you can only move after waiting for some time. The maximum wait time is the largest value for which you can still reach the safehouse before the fire. We can use binary search on the wait time, and for each candidate, simulate the fire and your movement using BFS.

Approach

  1. Use multi-source BFS to compute the earliest time the fire reaches each cell.
  2. Use binary search on the wait time (from 0 to a large value, e.g., 10^9).
  3. For each wait time, simulate your movement with BFS:
    • You can move to a cell if you arrive before or at the same time as the fire (but not after).
    • If you reach the safehouse before or at the same time as the fire, it's safe.
  4. If you can always reach the safehouse, return 10^9; if never, return -1; otherwise, return the maximum wait time found.

Code

Python
from collections import deque
class Solution:
    def maximumMinutes(self, grid: list[list[int]]) -> int:
        m, n = len(grid), len(grid[0])
        fire = [[float('inf')] * n for _ in range(m)]
        q = deque()
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    fire[i][j] = 0
                    q.append((i, j))
        dirs = [(-1,0),(1,0),(0,-1),(0,1)]
        # Multi-source BFS for fire
        while q:
            x, y = q.popleft()
            for dx, dy in dirs:
                nx, ny = x + dx, y + dy
                if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == 0 and fire[nx][ny] == float('inf'):
                    fire[nx][ny] = fire[x][y] + 1
                    q.append((nx, ny))
        def can_escape(wait):
            vis = [[-1]*n for _ in range(m)]
            q = deque([(0, 0, wait)])
            vis[0][0] = wait
            while q:
                x, y, t = q.popleft()
                if [x, y] == [m-1, n-1]:
                    if t <= fire[x][y]:
                        return True
                for dx, dy in dirs:
                    nx, ny = x + dx, y + dy
                    if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == 0:
                        nt = t + 1
                        if nt < fire[nx][ny] and (vis[nx][ny] == -1 or nt < vis[nx][ny]):
                            vis[nx][ny] = nt
                            q.append((nx, ny, nt))
                        # Special case: can arrive at safehouse at the same time as fire
                        if [nx, ny] == [m-1, n-1] and nt == fire[nx][ny] and (vis[nx][ny] == -1 or nt < vis[nx][ny]):
                            vis[nx][ny] = nt
                            q.append((nx, ny, nt))
            return False
        lo, hi, ans = 0, 10**9, -1
        while lo <= hi:
            mid = (lo + hi) // 2
            if can_escape(mid):
                ans = mid
                lo = mid + 1
            else:
                hi = mid - 1
        if ans >= 10**9:
            return 10**9
        return ans

Complexity

  • ⏰ Time complexity: O(mn log K), where K is the search range (up to 10^9), and each BFS is O(mn).
  • 🧺 Space complexity: O(mn) for the fire and visited arrays.

Comments