Problem

To estimate π using the Monte Carlo method, we’ll utilize the concept of randomly generating points within a square and determining how many fall inside a quarter circle.

Monte Carlo Method

Lets do the setup:

  • Imagine a square with side length 2 centered at the origin, with coordinates ranging from (-1, -1) to (1, 1).
  • Inside this square, there is a quarter circle of radius 1, also centered at the origin.
  • The area of the square is 4 (since side length is 2), and the area of the quarter circle is (πr^2 / 4 = π/4) (since r=1).

i.e. Let B be area of square, and A be area of circle $$ B = 4r^2 $$

$$ A = \pi r^2 $$

$$ \frac{A}{B} = \frac{\pi}{4} $$

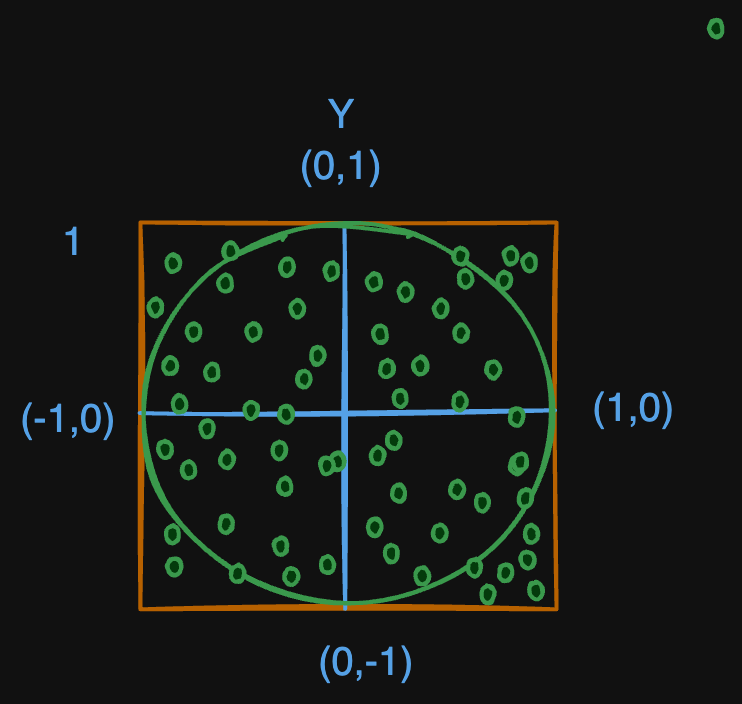
Now, we count the points

  • Generate random points within the square.
  • Count how many points fall inside the quarter circle.
  • The proportion of points inside the quarter circle to the total number of points approximates the ratio of the areas, (π/4).

Estimating Pi

Let N be the total number of points, and M be the number of points inside the quarter circle.

$$  \frac{M}{N} ≈ \frac{π}{4} $$ $$ \implies π ≈ 4 \cdot \frac{M}{N} $$

Code

Java

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import java.util.Random;


public class MonteCarloPi {

	public static void main(String[] args) {
		int numPoints = 1 _000_000;
		double piEstimate = estimatePi(numPoints);
		System.out.printf("Estimated π to 3 decimal places: %.3f%n", piEstimate);
	}

	public static double estimatePi(int numPoints) {
		int insideCircle = 0;
		Random rand = new Random();

		for (int i = 0; i < numPoints; i++) {
			double x = rand.nextDouble() * 2 - 1; // Generate x in [-1, 1]
			double y = rand.nextDouble() * 2 - 1; // Generate y in [-1, 1]
			if (x * x + y * y <= 1) {
				insideCircle += 1;
			}
		}

		return 4.0 * insideCircle / numPoints;
	}
}

Python

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

import random


def estimate_pi(num_points):
    inside_circle = 0

    for _ in range(num_points):
        x = random.uniform(-1, 1)
        y = random.uniform(-1, 1)

        if x**2 + y**2 <= 1:
            inside_circle += 1

    pi_estimate = 4 * inside_circle / num_points
    return pi_estimate


# Number of points to generate
num_points = 1_000_000
pi_estimate = estimate_pi(num_points)
print(f"Estimated π to 3 decimal places: {pi_estimate:.3f}")

Complexity

  • ⏰ Time complexity: O(n), where n is the number of random points generated.
  • 🧺 Space complexity: O(1)

Summary

The Monte Carlo method provides a simple yet effective way to estimate π by simulating random points within a specific range and calculating the ratio of points inside a quarter circle to the total number of points. The accuracy improves with an increase in the number of points generated.