Even Odd Tree

Problem

A binary tree is named Even-Odd if it meets the following conditions:

The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).

Given the root of a binary tree, returntrue _if the binary tree isEven-Odd , otherwise return _false .

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11



![](https://assets.leetcode.com/uploads/2020/09/15/sample_1_1966.png)

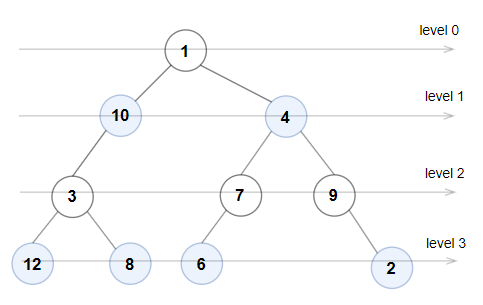
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
Output: true
Explanation: The node values on each level are:
Level 0: [1]
Level 1: [10,4]
Level 2: [3,7,9]
Level 3: [12,8,6,2]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10



![](https://assets.leetcode.com/uploads/2020/09/15/sample_2_1966.png)

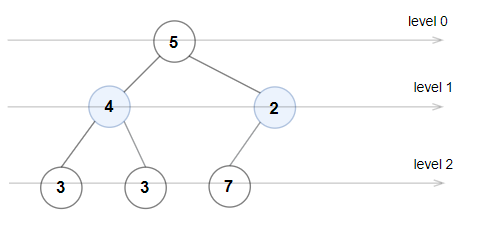
Input: root = [5,4,2,3,3,7]
Output: false
Explanation: The node values on each level are:
Level 0: [5]
Level 1: [4,2]
Level 2: [3,3,7]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.

Example 3

1
2
3
4
5
6



![](https://assets.leetcode.com/uploads/2020/09/22/sample_1_333_1966.png)

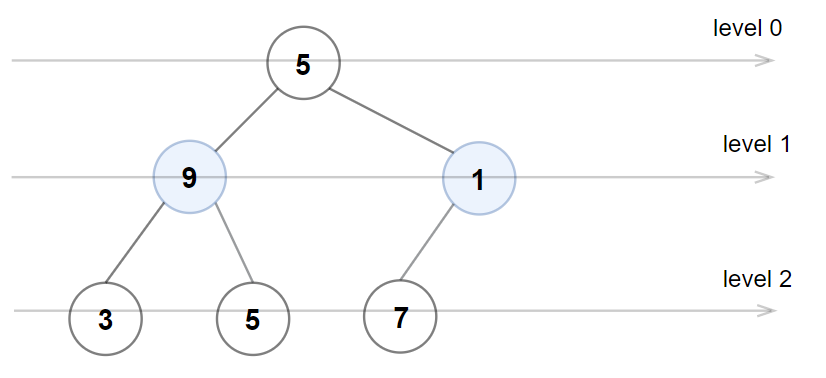
Input: root = [5,9,1,3,5,7]
Output: false
Explanation: Node values in the level 1 should be even integers.

Constraints

The number of nodes in the tree is in the range [1, 105].
1 <= Node.val <= 10^6

Solution

Method 1 – Level Order Traversal (BFS)

Intuition

We can use BFS to traverse the tree level by level. For each level, we check the parity and order of the node values according to the problem’s rules: even-indexed levels must have strictly increasing odd values, and odd-indexed levels must have strictly decreasing even values.

Approach

Use a queue to perform BFS, tracking the current level.
For each level:
- For even-indexed levels: check that all values are odd and strictly increasing from left to right.
- For odd-indexed levels: check that all values are even and strictly decreasing from left to right.
If any check fails, return False.
If all levels satisfy the conditions, return True.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution {
public:
    bool isEvenOddTree(TreeNode* root) {
        queue<TreeNode*> q;
        q.push(root);
        bool even = true;
        while (!q.empty()) {
            int sz = q.size();
            int prev = even ? INT_MIN : INT_MAX;
            for (int i = 0; i < sz; ++i) {
                TreeNode* node = q.front(); q.pop();
                int v = node->val;
                if (even) {
                    if (v % 2 == 0 || v <= prev) return false;
                } else {
                    if (v % 2 == 1 || v >= prev) return false;
                }
                prev = v;
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
            even = !even;
        }
        return true;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


class Solution {
    public boolean isEvenOddTree(TreeNode root) {
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        boolean even = true;
        while (!q.isEmpty()) {
            int sz = q.size();
            int prev = even ? Integer.MIN_VALUE : Integer.MAX_VALUE;
            for (int i = 0; i < sz; ++i) {
                TreeNode node = q.poll();
                int v = node.val;
                if (even) {
                    if (v % 2 == 0 || v <= prev) return false;
                } else {
                    if (v % 2 == 1 || v >= prev) return false;
                }
                prev = v;
                if (node.left != null) q.offer(node.left);
                if (node.right != null) q.offer(node.right);
            }
            even = !even;
        }
        return true;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


class Solution:
    def isEvenOddTree(self, root: 'TreeNode') -> bool:
        from collections import deque
        q = deque([root])
        even = True
        while q:
            sz = len(q)
            prev = float('-inf') if even else float('inf')
            for _ in range(sz):
                node = q.popleft()
                v = node.val
                if even:
                    if v % 2 == 0 or v <= prev:
                        return False
                else:
                    if v % 2 == 1 or v >= prev:
                        return False
                prev = v
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            even = not even
        return True

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


use std::collections::VecDeque;
impl Solution {
    pub fn is_even_odd_tree(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
        let mut q = VecDeque::new();
        if let Some(r) = root { q.push_back(r); }
        let mut even = true;
        while !q.is_empty() {
            let sz = q.len();
            let mut prev = if even { i32::MIN } else { i32::MAX };
            for _ in 0..sz {
                let node = q.pop_front().unwrap();
                let n = node.borrow();
                let v = n.val;
                if even {
                    if v % 2 == 0 || v <= prev { return false; }
                } else {
                    if v % 2 == 1 || v >= prev { return false; }
                }
                prev = v;
                if let Some(left) = n.left.clone() { q.push_back(left); }
                if let Some(right) = n.right.clone() { q.push_back(right); }
            }
            even = !even;
        }
        true
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


class Solution {
    isEvenOddTree(root: TreeNode | null): boolean {
        if (!root) return true;
        let q: TreeNode[] = [root];
        let even = true;
        while (q.length) {
            let sz = q.length;
            let prev = even ? -Infinity : Infinity;
            for (let i = 0; i < sz; ++i) {
                const node = q.shift()!;
                const v = node.val;
                if (even) {
                    if (v % 2 === 0 || v <= prev) return false;
                } else {
                    if (v % 2 === 1 || v >= prev) return false;
                }
                prev = v;
                if (node.left) q.push(node.left);
                if (node.right) q.push(node.right);
            }
            even = !even;
        }
        return true;
    }
}

Complexity

⏰ Time complexity: O(n), where n is the number of nodes in the tree (each node is visited once).
🧺 Space complexity: O(n), for the queue used in BFS.

Problem#

Examples#

Example 1#

Example 2#

Example 3#

Constraints#

Solution#

Method 1 – Level Order Traversal (BFS)#

Intuition#

Approach#

Code#

Complexity#