Extract Kth Character From The Rope Tree

Problem

You are given the root of a binary tree and an integer k. Besides the left and right children, every node of this tree has two other properties, a string node.val containing only lowercase English letters (possibly empty) and a non-negative integer node.len. There are two types of nodes in this tree:

• Leaf : These nodes have no children, node.len = 0, and node.val is some non-empty string.
• Internal : These nodes have at least one child (also at most two children), node.len > 0, and node.val is an empty string.

The tree described above is called a Rope binary tree. Now we define S[node] recursively as follows:

• If node is some leaf node, S[node] = node.val,
• Otherwise if node is some internal node, S[node] = concat(S[node.left], S[node.right]) and S[node].length = node.len.

Return k-th character of the string S[root].

Note: If s and p are two strings, concat(s, p) is a string obtained by concatenating p to s. For example, concat("ab", "zz") = "abzz".

Examples

Example 1:

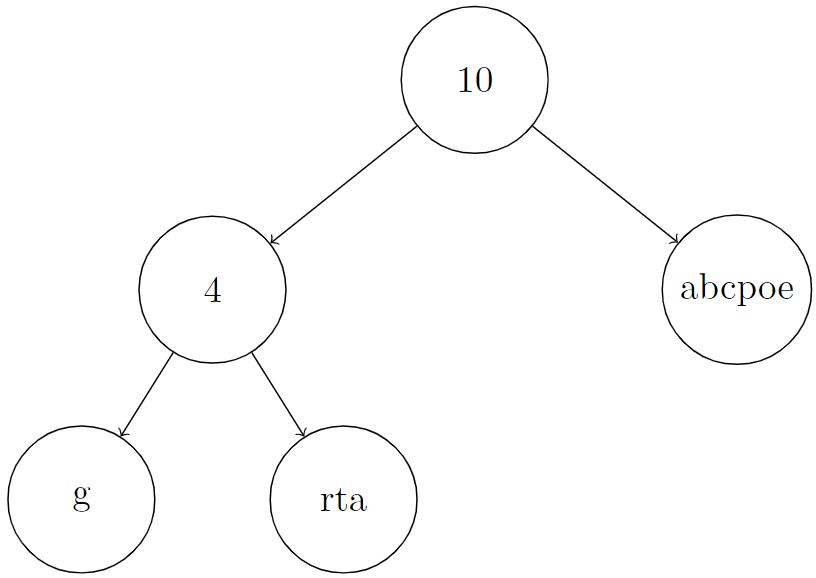
Input: root = [10,4,"abcpoe","g","rta"], k = 6
Output: "b"
Explanation: In the picture below, we put an integer on internal nodes that represents node.len, and a string on leaf nodes that represents node.val.
You can see that S[root] = concat(concat("g", "rta"), "abcpoe") = "grtaabcpoe". So S[root][5], which represents 6th character of it, is equal to "b".
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2600-2699/2689.Extract%20Kth%20Character%20From%20The%20Rope%20Tree/images/example1.png)

Example 2:

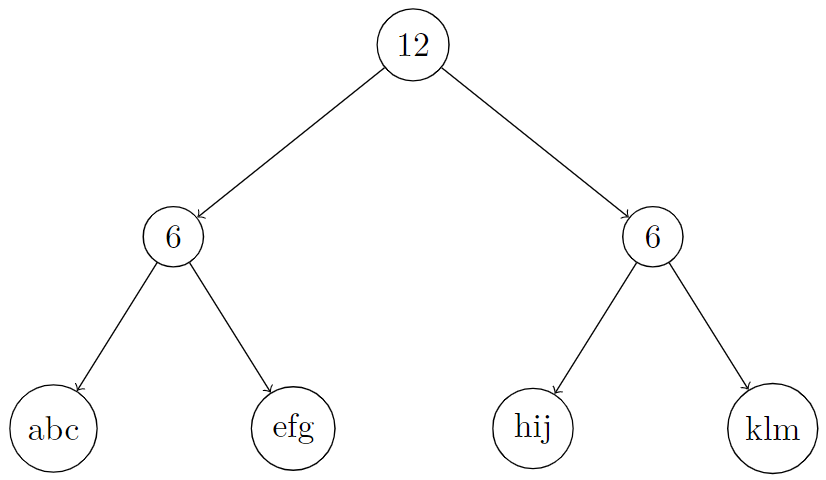
Input: root = [12,6,6,"abc","efg","hij","klm"], k = 3
Output: "c"
Explanation: In the picture below, we put an integer on internal nodes that represents node.len, and a string on leaf nodes that represents node.val.
You can see that S[root] = concat(concat("abc", "efg"), concat("hij", "klm")) = "abcefghijklm". So S[root][2], which represents the 3rd character of it, is equal to "c".
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2600-2699/2689.Extract%20Kth%20Character%20From%20The%20Rope%20Tree/images/example2.png)

Example 3:

Input: root = ["ropetree"], k = 8
Output: "e"
Explanation: In the picture below, we put an integer on internal nodes that represents node.len, and a string on leaf nodes that represents node.val.
You can see that S[root] = "ropetree". So S[root][7], which represents 8th character of it, is equal to "e".
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2600-2699/2689.Extract%20Kth%20Character%20From%20The%20Rope%20Tree/images/example3.png)

Constraints:

• The number of nodes in the tree is in the range [1, 103]
• node.val contains only lowercase English letters
• 0 <= node.val.length <= 50
• 0 <= node.len <= 10^4
• for leaf nodes, node.len = 0 and node.val is non-empty
• for internal nodes, node.len > 0 and node.val is empty
• 1 <= k <= S[root].length

Solution

Method 1 – Recursive Traversal Using Lengths

Intuition

The rope tree is designed so that each internal node's length is the sum of its children's strings. To find the k-th character, we can recursively decide whether to go left or right based on the lengths, without building the whole string.

Approach

1. At each node:
   • If it's a leaf, return the k-th character from its value.
   • Otherwise, check the length of the left subtree.
2. If k is less than or equal to the left subtree's length, recurse left.
3. Otherwise, subtract the left length and recurse right.
4. Continue until a leaf is reached.

Code

C++

class Solution {
public:
    char getKthCharacter(TreeNode* root, int k) {
        if (!root->left && !root->right) return root->val[k-1];
        int leftLen = root->left ? root->left->len : 0;
        if (k <= leftLen) return getKthCharacter(root->left, k);
        return getKthCharacter(root->right, k - leftLen);
    }
};

Go

func getKthCharacter(root *TreeNode, k int) byte {
    if root.Left == nil && root.Right == nil {
        return root.Val[k-1]
    }
    leftLen := 0
    if root.Left != nil {
        leftLen = root.Left.Len
    }
    if k <= leftLen {
        return getKthCharacter(root.Left, k)
    }
    return getKthCharacter(root.Right, k-leftLen)
}

Java

class Solution {
    public char getKthCharacter(TreeNode root, int k) {
        if (root.left == null && root.right == null)
            return root.val.charAt(k-1);
        int leftLen = root.left != null ? root.left.len : 0;
        if (k <= leftLen)
            return getKthCharacter(root.left, k);
        return getKthCharacter(root.right, k - leftLen);
    }
}

Kotlin

class Solution {
    fun getKthCharacter(root: TreeNode, k: Int): Char {
        if (root.left == null && root.right == null)
            return root.`val`[k-1]
        val leftLen = root.left?.len ?: 0
        return if (k <= leftLen)
            getKthCharacter(root.left!!, k)
        else
            getKthCharacter(root.right!!, k - leftLen)
    }
}

Python

class Solution:
    def getKthCharacter(self, root: 'TreeNode', k: int) -> str:
        if not root.left and not root.right:
            return root.val[k-1]
        left_len = root.left.len if root.left else 0
        if k <= left_len:
            return self.getKthCharacter(root.left, k)
        return self.getKthCharacter(root.right, k - left_len)

Rust

impl Solution {
    pub fn get_kth_character(root: &TreeNode, k: usize) -> char {
        if root.left.is_none() && root.right.is_none() {
            return root.val.chars().nth(k-1).unwrap();
        }
        let left_len = root.left.as_ref().map_or(0, |l| l.len);
        if k <= left_len {
            return Solution::get_kth_character(root.left.as_ref().unwrap(), k);
        }
        Solution::get_kth_character(root.right.as_ref().unwrap(), k - left_len)
    }
}

TypeScript

class Solution {
    getKthCharacter(root: TreeNode, k: number): string {
        if (!root.left && !root.right) return root.val[k-1];
        const leftLen = root.left ? root.left.len : 0;
        if (k <= leftLen) return this.getKthCharacter(root.left, k);
        return this.getKthCharacter(root.right, k - leftLen);
    }
}

Complexity

• ⏰ Time complexity: O(h), where h is the height of the tree, since we only traverse one path from root to leaf.
• 🧺 Space complexity: O(h), due to the recursion stack.