Falling Squares

Problem

There are several squares being dropped onto the X-axis of a 2D plane.

You are given a 2D integer array positions where positions[i] = [lefti, sideLengthi] represents the ith square with a side length of sideLengthi that is dropped with its left edge aligned with X-coordinate lefti.

Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands on the top side of another square or on the X-axis. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.

After each square is dropped, you must record the height of the current tallest stack of squares.

Return an integer array ans where ans[i] represents the height described above after dropping the ith square.

Examples

Example 1:

1
2
3
4
5
6
7


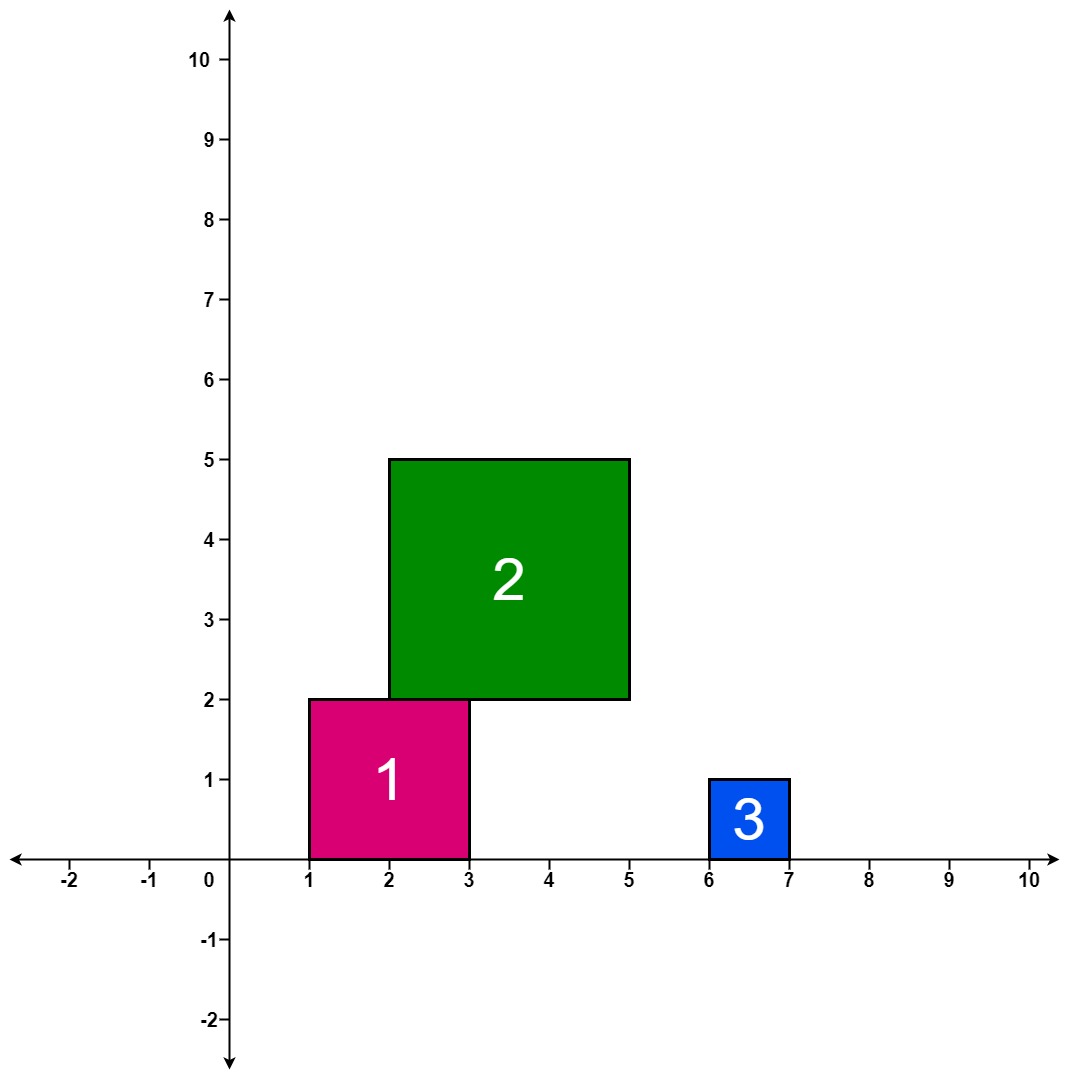
Input: positions = [[1,2],[2,3],[6,1]]
Output: [2,5,5]
Explanation:
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of [2, 5, 5].

Example 2:

1
2
3
4
5
6
7


Input: positions = [[100,100],[200,100]]
Output: [100,100]
Explanation:
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of [100, 100].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.

Solution

Method 1 - Using intervals

When a square is dropped onto the X-axis:

It will either land directly on the X-axis if there are no overlapping squares below it.
It will stack on top of an existing square if its position overlaps another square’s position vertically.

To solve this problem, we’ll maintain:

A running record of intervals representing landed squares where each interval denotes the range [lefti, lefti + sideLengthi] and its corresponding height.
For each square being dropped, we’ll compute the new height based on the overlapping intervals and update the running record.

Approach

Initialisation: Define an empty list to store the intervals and their heights, and an empty result list ans to store the tallest stack height after each square is dropped.
Iterate through each square in positions:
- Extract the current square’s left and sideLength.
- Determine the height from overlapping intervals using a sweep for intervals and find the maximum vertical height beneath the square.
- Update the result list ans with the tallest stack height after adding the new square.
- Update the intervals list with the current square’s position and new height.
Return the result list ans.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


class Solution {

    public List<Integer> fallingSquares(int[][] positions) {
        List<int[]> intervals = new ArrayList<>(); // Stores the intervals + heights
        List<Integer> ans = new ArrayList<>(); // Result to store heights after each drop
        int maxHeight = 0;

        for (int[] pos : positions) {
            int left = pos[0], side = pos[1];
            int right = left + side;
            int currHeight = side;

            // Check overlapping intervals
            for (int[] interval : intervals) {
                int l = interval[0], r = interval[1], h = interval[2];
                if (!(right <= l || left >= r)) { // Overlap
                    currHeight = Math.max(currHeight, h + side);
                }
            }

            // Update intervals
            intervals.add(new int[] { left, right, currHeight });
            maxHeight = Math.max(maxHeight, currHeight);
            ans.add(maxHeight);
        }

        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution:
    def fallingSquares(self, positions: List[List[int]]) -> List[int]:
        intervals = []  # Stores the current intervals and their heights
        ans: List[int] = []  # Result to store the height after each drop
        max_height = 0

        for left, side in positions:
            right = left + side
            curr_height = side
            
            # Check overlapping intervals
            for l, r, h in intervals:
                if not (right <= l or left >= r):  # Overlap situation
                    curr_height = max(curr_height, h + side)
            
            # Update intervals
            intervals.append((left, right, curr_height))
            max_height = max(max_height, curr_height)
            ans.append(max_height)
        
        return ans

Complexity

⏰ Time complexity: O(n^2). The outer loop iterates over positions, which has n elements.
- For each square, we iterate over the existing intervals to check overlap, which can also be n in the worst case.
🧺 Space complexity: O(n). We maintain the list of intervals with up to n entries, each storing [left, right, height].

Problem#

Examples#

Solution#

Method 1 - Using intervals#

Approach#

Code#

Complexity#