problemmediumalgorithmsleetcode-3537leetcode 3537leetcode3537

Fill a Special Grid

MediumUpdated: Jul 8, 2025
Practice on:
LeetCode

Problem

You are given a non-negative integer n representing a 2n x 2n grid. You must fill the grid with integers from 0 to 22n - 1 to make it special. A grid is special if it satisfies all the following conditions:

  • All numbers in the top-right quadrant are smaller than those in the bottom-right quadrant.
  • All numbers in the bottom-right quadrant are smaller than those in the bottom-left quadrant.
  • All numbers in the bottom-left quadrant are smaller than those in the top-left quadrant.
  • Each of its quadrants is also a special grid.

Return the special 2n x 2n grid.

Note : Any 1x1 grid is special.

Examples

Example 1

Input: n = 0
Output: [[0]]
Explanation:
The only number that can be placed is 0, and there is only one possible
position in the grid.

Example 2

Input: n = 1
Output: [[3,0],[2,1]]
Explanation:
The numbers in each quadrant are:
* Top-right: 0
* Bottom-right: 1
* Bottom-left: 2
* Top-left: 3

Since 0 < 1 < 2 < 3, this satisfies the given constraints.

Example 3

Input: n = 2
Output: [[15,12,3,0],[14,13,2,1],[11,8,7,4],[10,9,6,5]]
Explanation:

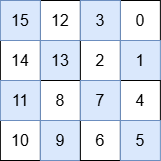The numbers in each quadrant are:

  • Top-right: 3, 0, 2, 1
  • Bottom-right: 7, 4, 6, 5
  • Bottom-left: 11, 8, 10, 9
  • Top-left: 15, 12, 14, 13
  • max(3, 0, 2, 1) < min(7, 4, 6, 5)
  • max(7, 4, 6, 5) < min(11, 8, 10, 9)
  • max(11, 8, 10, 9) < min(15, 12, 14, 13) This satisfies the first three requirements. Additionally, each quadrant is also a special grid. Thus, this is a special grid.

Constraints

  • 0 <= n <= 10

Solution

Method 1 – Divide and Conquer (Recursive Construction)

Intuition

The problem is recursive: each quadrant must itself be a special grid. We can fill the grid by recursively filling each quadrant with a range of numbers, ensuring the required order between quadrants. For a 2^n x 2^n grid, we split it into four quadrants, fill each recursively, and assign number ranges so that the top-right < bottom-right < bottom-left < top-left.

Approach

  1. If n == 0, return [start].
  2. For n > 0:
    • The grid size is 2^n x 2^n.
    • Divide the range [start, start + 4^n - 1] into four equal parts.
    • Recursively fill each quadrant:
      • Top-right: smallest numbers
      • Bottom-right: next smallest
      • Bottom-left: next
      • Top-left: largest
    • Place the quadrants in the correct positions in the grid.
  3. Return the constructed grid.

Code

C++
class Solution {
public:
    vector<vector<int>> construct(int n, int start) {
        int sz = 1 << n;
        if (n == 0) return {{start}};
        int len = sz / 2;
        int block = len * len;
        auto tr = construct(n-1, start);
        auto br = construct(n-1, start + block);
        auto bl = construct(n-1, start + 2*block);
        auto tl = construct(n-1, start + 3*block);
        vector<vector<int>> ans(sz, vector<int>(sz));
        for (int i = 0; i < len; ++i) {
            for (int j = 0; j < len; ++j) {
                ans[i][j+len] = tr[i][j];
                ans[i+len][j+len] = br[i][j];
                ans[i+len][j] = bl[i][j];
                ans[i][j] = tl[i][j];
            }
        }
        return ans;
    }
    vector<vector<int>> specialGrid(int n) {
        return construct(n, 0);
    }
};
Go
func construct(n, start int) [][]int {
    sz := 1 << n
    if n == 0 {
        return [][]int{{start}}
    }
    len := sz / 2
    block := len * len
    tr := construct(n-1, start)
    br := construct(n-1, start+block)
    bl := construct(n-1, start+2*block)
    tl := construct(n-1, start+3*block)
    ans := make([][]int, sz)
    for i := range ans {
        ans[i] = make([]int, sz)
    }
    for i := 0; i < len; i++ {
        for j := 0; j < len; j++ {
            ans[i][j+len] = tr[i][j]
            ans[i+len][j+len] = br[i][j]
            ans[i+len][j] = bl[i][j]
            ans[i][j] = tl[i][j]
        }
    }
    return ans
}
func specialGrid(n int) [][]int {
    return construct(n, 0)
}
Java
class Solution {
    private int[][] construct(int n, int start) {
        int sz = 1 << n;
        if (n == 0) return new int[][]{{start}};
        int len = sz / 2, block = len * len;
        int[][] tr = construct(n-1, start);
        int[][] br = construct(n-1, start+block);
        int[][] bl = construct(n-1, start+2*block);
        int[][] tl = construct(n-1, start+3*block);
        int[][] ans = new int[sz][sz];
        for (int i = 0; i < len; i++)
            for (int j = 0; j < len; j++) {
                ans[i][j+len] = tr[i][j];
                ans[i+len][j+len] = br[i][j];
                ans[i+len][j] = bl[i][j];
                ans[i][j] = tl[i][j];
            }
        return ans;
    }
    public int[][] specialGrid(int n) {
        return construct(n, 0);
    }
}
Kotlin
class Solution {
    fun specialGrid(n: Int): Array<IntArray> {
        fun construct(n: Int, start: Int): Array<IntArray> {
            val sz = 1 shl n
            if (n == 0) return arrayOf(intArrayOf(start))
            val len = sz / 2
            val block = len * len
            val tr = construct(n-1, start)
            val br = construct(n-1, start+block)
            val bl = construct(n-1, start+2*block)
            val tl = construct(n-1, start+3*block)
            val ans = Array(sz) { IntArray(sz) }
            for (i in 0 until len) for (j in 0 until len) {
                ans[i][j+len] = tr[i][j]
                ans[i+len][j+len] = br[i][j]
                ans[i+len][j] = bl[i][j]
                ans[i][j] = tl[i][j]
            }
            return ans
        }
        return construct(n, 0)
    }
}
Python
class Solution:
    def specialGrid(self, n: int) -> list[list[int]]:
        def construct(n: int, start: int) -> list[list[int]]:
            sz = 1 << n
            if n == 0:
                return [[start]]
            l = sz // 2
            block = l * l
            tr = construct(n-1, start)
            br = construct(n-1, start+block)
            bl = construct(n-1, start+2*block)
            tl = construct(n-1, start+3*block)
            ans = [[0]*sz for _ in range(sz)]
            for i in range(l):
                for j in range(l):
                    ans[i][j+l] = tr[i][j]
                    ans[i+l][j+l] = br[i][j]
                    ans[i+l][j] = bl[i][j]
                    ans[i][j] = tl[i][j]
            return ans
        return construct(n, 0)
Rust
impl Solution {
    pub fn special_grid(n: i32) -> Vec<Vec<i32>> {
        fn construct(n: i32, start: i32) -> Vec<Vec<i32>> {
            let sz = 1 << n;
            if n == 0 {
                return vec![vec![start]];
            }
            let l = sz / 2;
            let block = l * l;
            let tr = construct(n-1, start);
            let br = construct(n-1, start+block);
            let bl = construct(n-1, start+2*block);
            let tl = construct(n-1, start+3*block);
            let mut ans = vec![vec![0; sz as usize]; sz as usize];
            for i in 0..l {
                for j in 0..l {
                    ans[i as usize][(j+l) as usize] = tr[i as usize][j as usize];
                    ans[(i+l) as usize][(j+l) as usize] = br[i as usize][j as usize];
                    ans[(i+l) as usize][j as usize] = bl[i as usize][j as usize];
                    ans[i as usize][j as usize] = tl[i as usize][j as usize];
                }
            }
            ans
        }
        construct(n, 0)
    }
}
TypeScript
class Solution {
    specialGrid(n: number): number[][] {
        function construct(n: number, start: number): number[][] {
            const sz = 1 << n;
            if (n === 0) return [[start]];
            const l = sz / 2;
            const block = l * l;
            const tr = construct(n-1, start);
            const br = construct(n-1, start+block);
            const bl = construct(n-1, start+2*block);
            const tl = construct(n-1, start+3*block);
            const ans = Array.from({length: sz}, () => Array(sz).fill(0));
            for (let i = 0; i < l; i++) {
                for (let j = 0; j < l; j++) {
                    ans[i][j+l] = tr[i][j];
                    ans[i+l][j+l] = br[i][j];
                    ans[i+l][j] = bl[i][j];
                    ans[i][j] = tl[i][j];
                }
            }
            return ans;
        }
        return construct(n, 0);
    }
}

Complexity

  • ⏰ Time complexity: O(4^n), since each level of recursion creates 4 subproblems and the total number of cells is 4^n.
  • 🧺 Space complexity: O(4^n), for the grid and recursion stack.

Comments