Filling Bookcase Shelves

Problem

You are given an array books where books[i] = [thicknessi, heighti] indicates the thickness and height of the ith book. You are also given an integer shelfWidth.

We want to place these books in order onto bookcase shelves that have a total width shelfWidth.

We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to shelfWidth, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.

Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.

• For example, if we have an ordered list of 5 books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.

Return the minimum possible height that the total bookshelf can be after placing shelves in this manner.

Examples

Example 1:

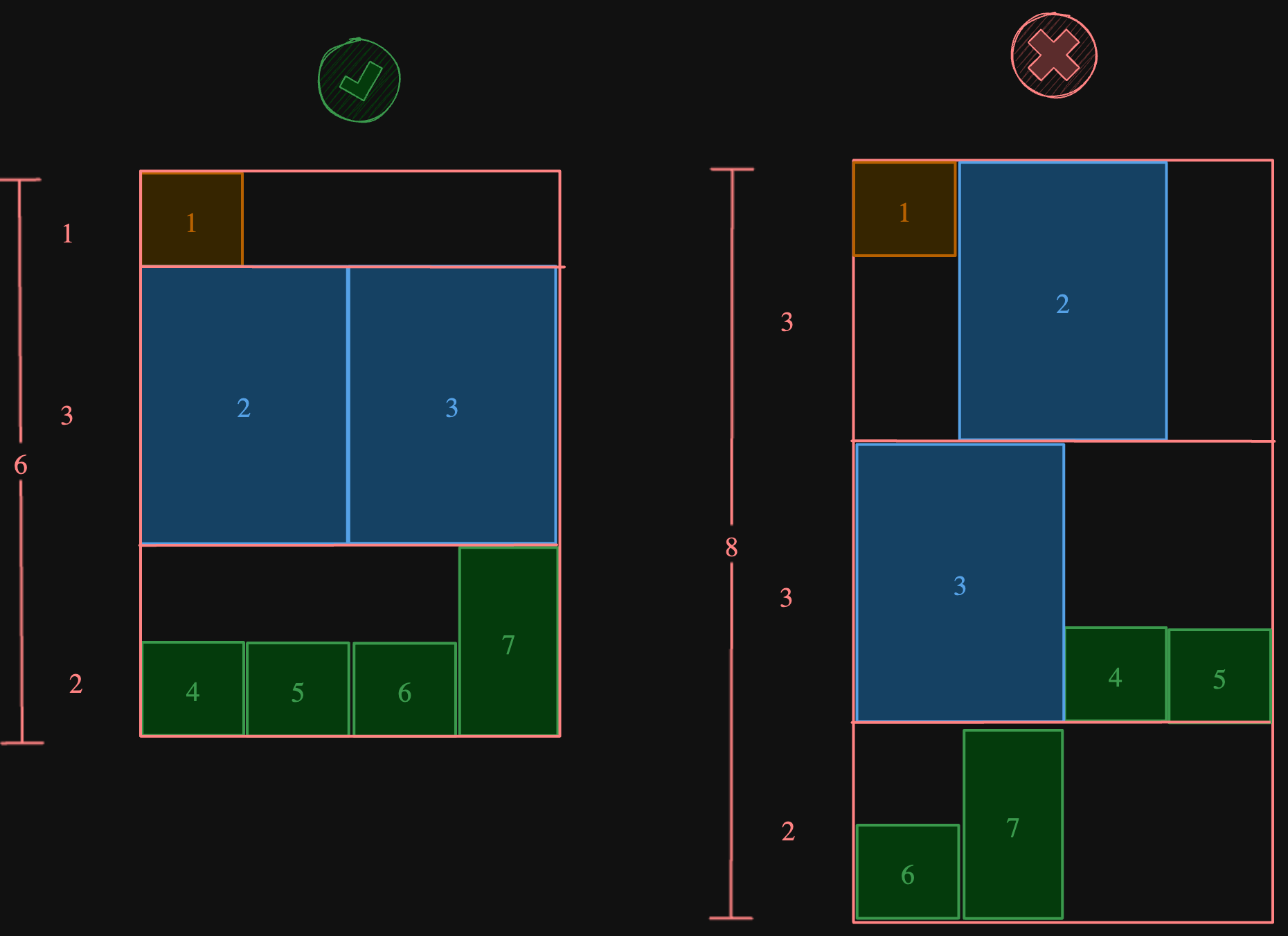
Input: books =[[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
Output: 6
Explanation:
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.

Example 2:

Input: books =[[1,3],[2,4],[3,2]], shelfWidth = 6
Output: 4

Solution

Method 1 - Recursion

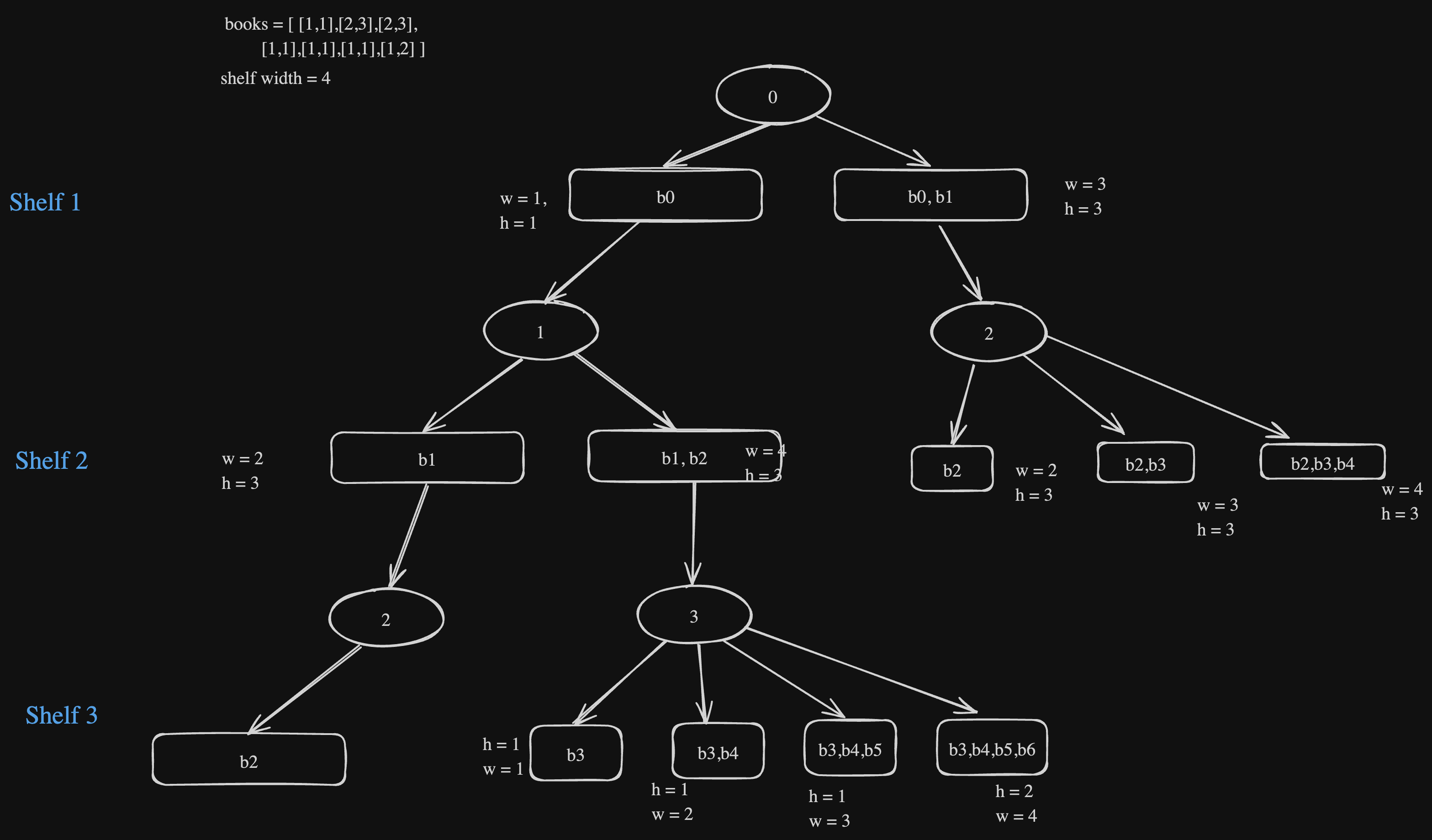
Try to place maximum books on the current shelf and call for the next shelf and maintain the minimum answer after placing every book on current shelf and return the minimum answer.

Now this leads to following cases:

4. Base Case: When all books are placed (i == n), return 0.
5. Recursive Case: Try placing books on the current shelf until the width exceeds shelfWidth, and recursively call dfs for the next book to find the total height required.

Here is the video explanation: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/W6owS3RNbUY" frameborder="0" allowfullscreen></iframe></div>

Code

C++

#include <vector>
#include <limits>
using namespace std;

class Solution {
 public:
  int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {
    return dfs(books, shelfWidth, 0);
  }

 private:
  int dfs(const vector<vector<int>>& books, int shelfWidth, int i) {
    int n = books.size();
    if (i == n) return 0;
    int width = 0;
    int height = 0;
    int minHeight = numeric_limits<int>::max();
    for (int j = i; j < n; ++j) {
      width += books[j][0];
      if (width > shelfWidth) break;
      height = max(height, books[j][1]);
      minHeight = min(minHeight, height + dfs(books, shelfWidth, j + 1));
    }
    return minHeight;
  }
};

Java

class Solution {

    public int minHeightShelves(int[][] books, int shelfWidth) {
        return dfs(books, shelfWidth, 0);
    }

    private int dfs(int[][] books, int shelfWidth, int i) {
        if (i == books.length) {
            return 0;
        }

        int width = 0;
        int height = 0;
        int minHeight = Integer.MAX_VALUE;

        for (int j = i; j < books.length; j++) {
            width += books[j][0];

            if (width > shelfWidth) {
                break;
            }

            height = Math.max(height, books[j][1]);
            minHeight = Math.min(minHeight, height + dfs(books, shelfWidth, j + 1));
        }

        return minHeight;
    }

}

Python

class Solution:
    def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:
        n = len(books)

        def dfs(i: int) -> int:
            if i == n:
                return 0
            width = 0
            height = 0
            min_height = 10**18
            for j in range(i, n):
                width += books[j][0]
                if width > shelfWidth:
                    break
                height = max(height, books[j][1])
                min_height = min(min_height, height + dfs(j + 1))
            return min_height

        return dfs(0)

Complexity

• ⏰ Time complexity: O(2^n) for exploring each subsets of books
• 🧺 Space complexity: O(n) for using recursion stack

Dry Run

Method 2 - Top Down DP

Recursion might result in overlapping subproblems. We can store results of subproblems to avoid redundant calculations, thus optimizing the recursive solution with memoization.

Code

C++

#include <vector>
#include <unordered_map>
#include <limits>
using namespace std;

class Solution {
 public:
	int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {
		memo.clear();
		this->books = books;
		this->shelfWidth = shelfWidth;
		return dfs(0);
	}

 private:
	unordered_map<int,int> memo;
	vector<vector<int>> books;
	int shelfWidth;

	int dfs(int i) {
		int n = books.size();
		if (i == n) return 0;
		if (memo.count(i)) return memo[i];
		int width = 0;
		int height = 0;
		int minHeight = numeric_limits<int>::max();
		for (int j = i; j < n; ++j) {
			width += books[j][0];
			if (width > shelfWidth) break;
			height = max(height, books[j][1]);
			minHeight = min(minHeight, height + dfs(j + 1));
		}
		memo[i] = minHeight;
		return minHeight;
	}
};

Java

class Solution {

	private Map<Integer, Integer> memo;

	public int minHeightShelves(int[][] books, int shelfWidth) {
		memo = new HashMap<>();
		return dfs(books, shelfWidth, 0);
	}

	private int dfs(int[][] books, int shelfWidth, int i) {
		if (i == books.length) {
			return 0;
		}

		if (memo.containsKey(i)) {
			return memo.get(i);
		}

		int width = 0;
		int height = 0;
		int minHeight = Integer.MAX_VALUE;

		for (int j = i; j < books.length; j++) {
			width += books[j][0];

			if (width > shelfWidth) {
				break;
			}

			height = Math.max(height, books[j][1]);
			minHeight = Math.min(minHeight, height + dfs(books, shelfWidth, j + 1));
		}

		memo.put(i, minHeight);
		return minHeight;
	}

}

Python

class Solution:
		def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:
				n = len(books)
				memo = {}

				def dfs(i: int) -> int:
						if i == n:
								return 0
						if i in memo:
								return memo[i]
						width = 0
						height = 0
						min_height = 10**18
						for j in range(i, n):
								width += books[j][0]
								if width > shelfWidth:
										break
								height = max(height, books[j][1])
								min_height = min(min_height, height + dfs(j + 1))
						memo[i] = min_height
						return min_height

				return dfs(0)

Complexity

• ⏰ Time complexity: O(n^2)
• 🧺 Space complexity: O(n) for using recursion stack

Method 3 - Bottom up DP

Here are the points for bottom up DP:

1. DP Array Initialization: dp array where dp[i] represents the minimum height needed to place the first i books.
2. Iterate Over Books: For each book, try placing it on the current shelf or start a new shelf, and update dp array accordingly.
3. Result: Return dp[n], representing the minimum height for placing all n books.

Code

C++

#include <vector>
#include <limits>
using namespace std;

class Solution {
 public:
  int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {
    int n = books.size();
    vector<int> dp(n+1, 0);
    dp[0] = 0;
    for (int i = 1; i <= n; ++i) {
      int width = 0;
      int height = 0;
      dp[i] = numeric_limits<int>::max();
      for (int j = i - 1; j >= 0; --j) {
        width += books[j][0];
        if (width > shelfWidth) break;
        height = max(height, books[j][1]);
        dp[i] = min(dp[i], dp[j] + height);
      }
    }
    return dp[n];
  }
};

Java

class Solution {

	public int minHeightShelves(int[][] books, int shelfWidth) {
		int n = books.length;
		int[] dp = new int[n + 1];
		dp[0] = 0;

		for (int i = 1; i <= n; i++) {
			int width = 0;
			int height = 0;
			dp[i] = Integer.MAX_VALUE;

			for (int j = i - 1; j >= 0; j--) {
				width += books[j][0];

				if (width > shelfWidth) {
					break;
				}

				height = Math.max(height, books[j][1]);
				dp[i] = Math.min(dp[i], dp[j] + height);
			}
		}

		return dp[n];

	}

}

Python

class Solution:
    def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:
        n = len(books)
        dp = [0] * (n + 1)
        for i in range(1, n + 1):
            width = 0
            height = 0
            dp[i] = 10**18
            for j in range(i-1, -1, -1):
                width += books[j][0]
                if width > shelfWidth:
                    break
                height = max(height, books[j][1])
                dp[i] = min(dp[i], dp[j] + height)
        return dp[n]

Complexity

• ⏰ Time complexity: O(n^2)
• 🧺 Space complexity: O(n) for using dp[] array