Find a Peak Element II
Problem
A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.
Given a 0-indexed m x n matrix mat where no two adjacent cells are equal , find any peak element mat[i][j] and return the length 2 array[i,j].
You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.
You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.
Examples
Example 1
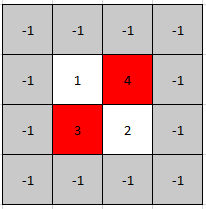
Input: mat = [[1,4],[3,2]]
Output: [0,1]
Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.
Example 2
**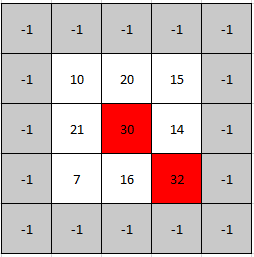**
Input: mat = [[10,20,15],[21,30,14],[7,16,32]]
Output: [1,1]
Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.
Constraints
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 10^5- No two adjacent cells are equal.
Solution
Method 1 – Binary Search on Columns
Intuition
Since each cell is only compared to its four neighbors and the matrix is surrounded by -1, a peak must exist. We can use binary search on columns: for each middle column, find the row with the maximum value, and check if it's a peak. If not, move to the side with the greater neighbor. This gives O(m log n) time.
Approach
- Set
left = 0,right = n - 1(columns). - While
left <= right:- Let
mid = (left + right) // 2. - Find the row
max_rowwith the maximum value in columnmid. - Compare
mat[max_row][mid]with its left and right neighbors (treat out-of-bounds as -1). - If it's greater than both, return
[max_row, mid]. - If the left neighbor is greater, search left half (
right = mid - 1). - If the right neighbor is greater, search right half (
left = mid + 1).
- Let
Code
C++
class Solution {
public:
vector<int> findPeakGrid(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
int max_row = 0;
for (int i = 1; i < m; ++i) {
if (mat[i][mid] > mat[max_row][mid]) max_row = i;
}
int left = mid > 0 ? mat[max_row][mid-1] : -1;
int right = mid < n-1 ? mat[max_row][mid+1] : -1;
if (mat[max_row][mid] > left && mat[max_row][mid] > right)
return {max_row, mid};
else if (left > mat[max_row][mid])
r = mid - 1;
else
l = mid + 1;
}
return {-1, -1};
}
};
Go
func findPeakGrid(mat [][]int) []int {
m, n := len(mat), len(mat[0])
l, r := 0, n-1
for l <= r {
mid := (l + r) / 2
maxRow := 0
for i := 1; i < m; i++ {
if mat[i][mid] > mat[maxRow][mid] {
maxRow = i
}
}
left := -1
if mid > 0 {
left = mat[maxRow][mid-1]
}
right := -1
if mid < n-1 {
right = mat[maxRow][mid+1]
}
if mat[maxRow][mid] > left && mat[maxRow][mid] > right {
return []int{maxRow, mid}
} else if left > mat[maxRow][mid] {
r = mid - 1
} else {
l = mid + 1
}
}
return []int{-1, -1}
}
Java
class Solution {
public int[] findPeakGrid(int[][] mat) {
int m = mat.length, n = mat[0].length;
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
int maxRow = 0;
for (int i = 1; i < m; i++) {
if (mat[i][mid] > mat[maxRow][mid]) maxRow = i;
}
int left = mid > 0 ? mat[maxRow][mid-1] : -1;
int right = mid < n-1 ? mat[maxRow][mid+1] : -1;
if (mat[maxRow][mid] > left && mat[maxRow][mid] > right)
return new int[]{maxRow, mid};
else if (left > mat[maxRow][mid])
r = mid - 1;
else
l = mid + 1;
}
return new int[]{-1, -1};
}
}
Kotlin
class Solution {
fun findPeakGrid(mat: Array<IntArray>): IntArray {
val m = mat.size
val n = mat[0].size
var l = 0
var r = n - 1
while (l <= r) {
val mid = (l + r) / 2
var maxRow = 0
for (i in 1 until m) {
if (mat[i][mid] > mat[maxRow][mid]) maxRow = i
}
val left = if (mid > 0) mat[maxRow][mid-1] else -1
val right = if (mid < n-1) mat[maxRow][mid+1] else -1
if (mat[maxRow][mid] > left && mat[maxRow][mid] > right)
return intArrayOf(maxRow, mid)
else if (left > mat[maxRow][mid])
r = mid - 1
else
l = mid + 1
}
return intArrayOf(-1, -1)
}
}
Python
class Solution:
def findPeakGrid(self, mat: list[list[int]]) -> list[int]:
m, n = len(mat), len(mat[0])
l, r = 0, n - 1
while l <= r:
mid = (l + r) // 2
max_row = max(range(m), key=lambda i: mat[i][mid])
left = mat[max_row][mid-1] if mid > 0 else -1
right = mat[max_row][mid+1] if mid < n-1 else -1
if mat[max_row][mid] > left and mat[max_row][mid] > right:
return [max_row, mid]
elif left > mat[max_row][mid]:
r = mid - 1
else:
l = mid + 1
return [-1, -1]
Rust
impl Solution {
pub fn find_peak_grid(mat: Vec<Vec<i32>>) -> Vec<i32> {
let m = mat.len();
let n = mat[0].len();
let (mut l, mut r) = (0, n - 1);
while l <= r {
let mid = (l + r) / 2;
let mut max_row = 0;
for i in 1..m {
if mat[i][mid] > mat[max_row][mid] {
max_row = i;
}
}
let left = if mid > 0 { mat[max_row][mid-1] } else { -1 };
let right = if mid < n-1 { mat[max_row][mid+1] } else { -1 };
if mat[max_row][mid] > left && mat[max_row][mid] > right {
return vec![max_row as i32, mid as i32];
} else if left > mat[max_row][mid] {
r = mid - 1;
} else {
l = mid + 1;
}
}
vec![-1, -1]
}
}
TypeScript
class Solution {
findPeakGrid(mat: number[][]): number[] {
const m = mat.length, n = mat[0].length;
let l = 0, r = n - 1;
while (l <= r) {
const mid = Math.floor((l + r) / 2);
let maxRow = 0;
for (let i = 1; i < m; i++) {
if (mat[i][mid] > mat[maxRow][mid]) maxRow = i;
}
const left = mid > 0 ? mat[maxRow][mid-1] : -1;
const right = mid < n-1 ? mat[maxRow][mid+1] : -1;
if (mat[maxRow][mid] > left && mat[maxRow][mid] > right)
return [maxRow, mid];
else if (left > mat[maxRow][mid])
r = mid - 1;
else
l = mid + 1;
}
return [-1, -1];
}
}
Complexity
- ⏰ Time complexity:
O(m log n), where m is the number of rows and n is the number of columns. Each binary search step scans all rows. - 🧺 Space complexity:
O(1), only a few variables are used.