Find a Safe Walk Through a Grid
Problem
You are given an m x n binary matrix grid and an integer health.
You start on the upper-left corner (0, 0) and would like to get to the lower-right corner (m - 1, n - 1).
You can move up, down, left, or right from one cell to another adjacent cell as long as your health remains positive.
Cells (i, j) with grid[i][j] = 1 are considered unsafe and reduce your health by 1.
Return true if you can reach the final cell with a health value of 1 or more, and false otherwise.
Examples
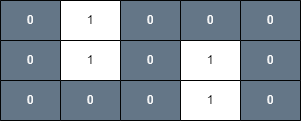
Example 1
Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]], health = 1
Output: true
Explanation:
The final cell can be reached safely by walking along the gray cells below.
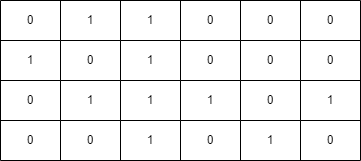
Example 2
Input: grid = [[0,1,1,0,0,0],[1,0,1,0,0,0],[0,1,1,1,0,1],[0,0,1,0,1,0]],
health = 3
Output: false
Explanation:
A minimum of 4 health points is needed to reach the final cell safely.
Example 3
Input: grid = [[1,1,1],[1,0,1],[1,1,1]], health = 5
Output: true
Explanation:
The final cell can be reached safely by walking along the gray cells below.
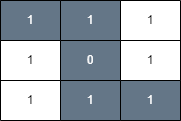
Any path that does not go through the cell `(1, 1)` is unsafe since your
health will drop to 0 when reaching the final cell.
Constraints
m == grid.lengthn == grid[i].length1 <= m, n <= 502 <= m * n1 <= health <= m + ngrid[i][j]is either 0 or 1.
Solution
Method 1 �� Dijkstra's Algorithm (BFS with Priority Queue)
Intuition
We want to reach the bottom-right cell with health ≥ 1, minimizing the number of unsafe cells (1s) we pass through. Each unsafe cell reduces health by 1. We can use a priority queue (min-heap) to always expand the path with the most remaining health, similar to Dijkstra's algorithm.
Approach
- Use a max-heap (priority queue) to store (remaining health, row, col).
- Start from (0, 0) with initial health.
- For each cell, try moving in all four directions.
- If the next cell is unsafe, reduce health by 1.
- Only visit a cell if we reach it with more health than any previous visit.
- If we reach (m-1, n-1) with health ≥ 1, return True.
- If the queue is empty, return False.
Code
C++
class Solution {
public:
bool isSafeWalk(vector<vector<int>>& grid, int health) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> best(m, vector<int>(n, -1));
priority_queue<tuple<int,int,int>> pq;
pq.emplace(health, 0, 0);
best[0][0] = health;
vector<pair<int,int>> dirs = {{0,1},{1,0},{0,-1},{-1,0}};
while (!pq.empty()) {
auto [h, x, y] = pq.top(); pq.pop();
if (x == m-1 && y == n-1 && h >= 1) return true;
for (auto [dx, dy] : dirs) {
int nx = x + dx, ny = y + dy;
if (nx < 0 || ny < 0 || nx >= m || ny >= n) continue;
int nh = h - grid[nx][ny];
if (nh < 1 || nh <= best[nx][ny]) continue;
best[nx][ny] = nh;
pq.emplace(nh, nx, ny);
}
}
return false;
}
};
Go
import "container/heap"
type Item struct{h, x, y int}
type PQ []Item
func (pq PQ) Len() int { return len(pq) }
func (pq PQ) Less(i, j int) bool { return pq[i].h > pq[j].h }
func (pq PQ) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq *PQ) Push(x any) { *pq = append(*pq, x.(Item)) }
func (pq *PQ) Pop() any { old := *pq; n := len(old); x := old[n-1]; *pq = old[:n-1]; return x }
func isSafeWalk(grid [][]int, health int) bool {
m, n := len(grid), len(grid[0])
best := make([][]int, m)
for i := range best { best[i] = make([]int, n); for j := range best[i] { best[i][j] = -1 } }
pq := &PQ{}
heap.Init(pq)
heap.Push(pq, Item{health, 0, 0})
best[0][0] = health
dirs := [][2]int{{0,1},{1,0},{0,-1},{-1,0}}
for pq.Len() > 0 {
cur := heap.Pop(pq).(Item)
if cur.x == m-1 && cur.y == n-1 && cur.h >= 1 { return true }
for _, d := range dirs {
nx, ny := cur.x+d[0], cur.y+d[1]
if nx < 0 || ny < 0 || nx >= m || ny >= n { continue }
nh := cur.h - grid[nx][ny]
if nh < 1 || nh <= best[nx][ny] { continue }
best[nx][ny] = nh
heap.Push(pq, Item{nh, nx, ny})
}
}
return false
}
Java
import java.util.*;
class Solution {
public boolean isSafeWalk(int[][] grid, int health) {
int m = grid.length, n = grid[0].length;
int[][] best = new int[m][n];
for (int[] row : best) Arrays.fill(row, -1);
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> b[0]-a[0]);
pq.offer(new int[]{health, 0, 0});
best[0][0] = health;
int[][] dirs = {{0,1},{1,0},{0,-1},{-1,0}};
while (!pq.isEmpty()) {
int[] cur = pq.poll();
int h = cur[0], x = cur[1], y = cur[2];
if (x == m-1 && y == n-1 && h >= 1) return true;
for (int[] d : dirs) {
int nx = x + d[0], ny = y + d[1];
if (nx < 0 || ny < 0 || nx >= m || ny >= n) continue;
int nh = h - grid[nx][ny];
if (nh < 1 || nh <= best[nx][ny]) continue;
best[nx][ny] = nh;
pq.offer(new int[]{nh, nx, ny});
}
}
return false;
}
}
Kotlin
import java.util.PriorityQueue
class Solution {
fun isSafeWalk(grid: Array<IntArray>, health: Int): Boolean {
val m = grid.size
val n = grid[0].size
val best = Array(m) { IntArray(n) { -1 } }
val pq = PriorityQueue(compareByDescending<Triple<Int,Int,Int>> { it.first })
pq.add(Triple(health, 0, 0))
best[0][0] = health
val dirs = arrayOf(0 to 1, 1 to 0, 0 to -1, -1 to 0)
while (pq.isNotEmpty()) {
val (h, x, y) = pq.poll()
if (x == m-1 && y == n-1 && h >= 1) return true
for ((dx, dy) in dirs) {
val nx = x + dx
val ny = y + dy
if (nx !in 0 until m || ny !in 0 until n) continue
val nh = h - grid[nx][ny]
if (nh < 1 || nh <= best[nx][ny]) continue
best[nx][ny] = nh
pq.add(Triple(nh, nx, ny))
}
}
return false
}
}
Python
import heapq
class Solution:
def isSafeWalk(self, grid: list[list[int]], health: int) -> bool:
m, n = len(grid), len(grid[0])
best = [[-1]*n for _ in range(m)]
heap = [(-health, 0, 0)]
best[0][0] = health
while heap:
neg_h, x, y = heapq.heappop(heap)
h = -neg_h
if x == m-1 and y == n-1 and h >= 1:
return True
for dx, dy in ((0,1),(1,0),(0,-1),(-1,0)):
nx, ny = x+dx, y+dy
if 0 <= nx < m and 0 <= ny < n:
nh = h - grid[nx][ny]
if nh < 1 or nh <= best[nx][ny]:
continue
best[nx][ny] = nh
heapq.heappush(heap, (-nh, nx, ny))
return False
Rust
use std::collections::BinaryHeap;
impl Solution {
pub fn is_safe_walk(grid: Vec<Vec<i32>>, health: i32) -> bool {
let m = grid.len();
let n = grid[0].len();
let mut best = vec![vec![-1; n]; m];
let mut heap = BinaryHeap::new();
heap.push((health, 0, 0));
best[0][0] = health;
let dirs = [(0,1),(1,0),(0,-1),(-1,0)];
while let Some((h, x, y)) = heap.pop() {
if x == m-1 && y == n-1 && h >= 1 { return true; }
for (dx, dy) in dirs.iter() {
let nx = x as i32 + dx;
let ny = y as i32 + dy;
if nx < 0 || ny < 0 || nx >= m as i32 || ny >= n as i32 { continue; }
let nx = nx as usize;
let ny = ny as usize;
let nh = h - grid[nx][ny];
if nh < 1 || nh <= best[nx][ny] { continue; }
best[nx][ny] = nh;
heap.push((nh, nx, ny));
}
}
false
}
}
TypeScript
class Solution {
isSafeWalk(grid: number[][], health: number): boolean {
const m = grid.length, n = grid[0].length;
const best = Array.from({length: m}, () => Array(n).fill(-1));
const heap: [number, number, number][] = [[-health, 0, 0]];
best[0][0] = health;
while (heap.length) {
heap.sort((a, b) => a[0] - b[0]);
const [neg_h, x, y] = heap.shift()!;
const h = -neg_h;
if (x === m-1 && y === n-1 && h >= 1) return true;
for (const [dx, dy] of [[0,1],[1,0],[0,-1],[-1,0]]) {
const nx = x + dx, ny = y + dy;
if (nx < 0 || ny < 0 || nx >= m || ny >= n) continue;
const nh = h - grid[nx][ny];
if (nh < 1 || nh <= best[nx][ny]) continue;
best[nx][ny] = nh;
heap.push([-nh, nx, ny]);
}
}
return false;
}
}
Complexity
- ⏰ Time complexity:
O(mn log(mn)), where m and n are the grid dimensions. Each cell can be pushed to the heap once per possible health value. - 🧺 Space complexity:
O(mn), for the best health matrix and the heap.