Find Edges in Shortest Paths
HardUpdated: Aug 2, 2025
Practice on:
Problem
You are given an undirected weighted graph of n nodes numbered from 0 to `n
- 1
. The graph consists ofmedges represented by a 2D arrayedges, whereedges[i] = [ai, bi, wi]indicates that there is an edge between nodesaiandbiwith weightwi`.
Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise,
answer[i] is false.
Return the array answer.
Note that the graph may not be connected.
Examples
Example 1
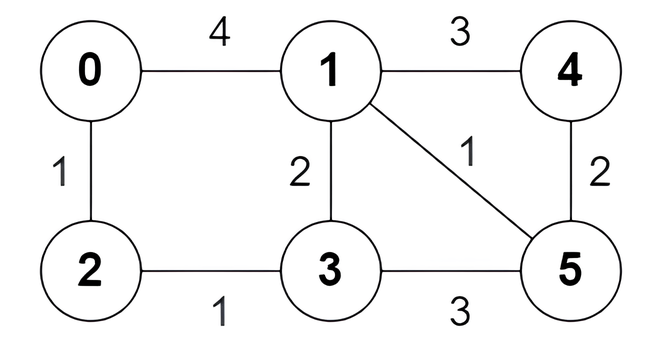
Input: n = 6, edges =
[[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]
Output: [true,true,true,false,true,true,true,false]
Explanation:
The following are **all** the shortest paths between nodes 0 and 5:
* The path `0 -> 1 -> 5`: The sum of weights is `4 + 1 = 5`.
* The path `0 -> 2 -> 3 -> 5`: The sum of weights is `1 + 1 + 3 = 5`.
* The path `0 -> 2 -> 3 -> 1 -> 5`: The sum of weights is `1 + 1 + 2 + 1 = 5`.
Example 2
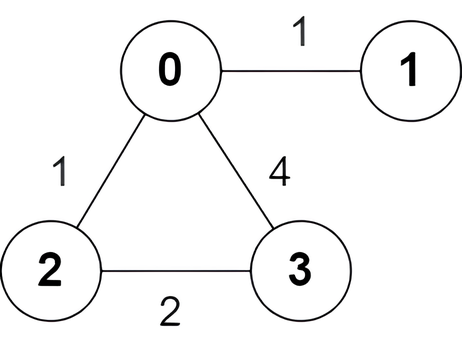
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]
Output: [true,false,false,true]
Explanation:
There is one shortest path between nodes 0 and 3, which is the path `0 -> 2 ->
3` with the sum of weights `1 + 2 = 3`.
Constraints
2 <= n <= 5 * 10^4m == edges.length1 <= m <= min(5 * 104, n * (n - 1) / 2)0 <= ai, bi < nai != bi1 <= wi <= 10^5- There are no repeated edges.
Solution
Method 1 – Dijkstra + Path Backtracking 1
Intuition
To determine if an edge is part of any shortest path from node 0 to node n-1, we can use Dijkstra's algorithm to find shortest distances, then check for each edge if it can be used in a shortest path by verifying if the sum of distances and edge weight equals the shortest path length.
Approach
- Build the adjacency list from the edge list.
- Run Dijkstra's algorithm from node 0 to get the shortest distance to all nodes (
dist_from_start). - Run Dijkstra's algorithm from node n-1 to get the shortest distance to all nodes (
dist_to_end). - The shortest path length from 0 to n-1 is
dist_from_start[n-1]. - For each edge [u, v, w], check if
dist_from_start[u] + w + dist_to_end[v] == shortestordist_from_start[v] + w + dist_to_end[u] == shortest. If so, mark answer[i] as true.
Code
C++
class Solution {
public:
vector<bool> findAnswer(int n, vector<vector<int>>& edges) {
vector<vector<pair<int,int>>> g(n);
for (int i = 0; i < edges.size(); ++i) {
int u = edges[i][0], v = edges[i][1], w = edges[i][2];
g[u].push_back({v, w});
g[v].push_back({u, w});
}
auto dijkstra = [&](int src) {
vector<long long> d(n, 1e18);
d[src] = 0;
priority_queue<pair<long long,int>, vector<pair<long long,int>>, greater<>> pq;
pq.push({0, src});
while (!pq.empty()) {
auto [du, u] = pq.top(); pq.pop();
if (du > d[u]) continue;
for (auto [v, w] : g[u]) {
if (d[v] > d[u] + w) {
d[v] = d[u] + w;
pq.push({d[v], v});
}
}
}
return d;
};
auto d1 = dijkstra(0), d2 = dijkstra(n-1);
long long shortest = d1[n-1];
vector<bool> ans(edges.size());
for (int i = 0; i < edges.size(); ++i) {
int u = edges[i][0], v = edges[i][1], w = edges[i][2];
if (d1[u] + w + d2[v] == shortest || d1[v] + w + d2[u] == shortest)
ans[i] = true;
}
return ans;
}
};
Go
func findAnswer(n int, edges [][]int) []bool {
g := make([][][2]int, n)
for i, e := range edges {
u, v, w := e[0], e[1], e[2]
g[u] = append(g[u], [2]int{v, w})
g[v] = append(g[v], [2]int{u, w})
}
dijkstra := func(src int) []int {
d := make([]int, n)
for i := range d {
d[i] = 1<<60
}
d[src] = 0
pq := &heapInt{{0, src}}
for pq.Len() > 0 {
du, u := heap.Pop(pq).([2]int)[0], heap.Pop(pq).([2]int)[1]
if du > d[u] {
continue
}
for _, vw := range g[u] {
v, w := vw[0], vw[1]
if d[v] > d[u]+w {
d[v] = d[u]+w
heap.Push(pq, [2]int{d[v], v})
}
}
}
return d
}
d1, d2 := dijkstra(0), dijkstra(n-1)
shortest := d1[n-1]
ans := make([]bool, len(edges))
for i, e := range edges {
u, v, w := e[0], e[1], e[2]
if d1[u]+w+d2[v] == shortest || d1[v]+w+d2[u] == shortest {
ans[i] = true
}
}
return ans
}
Java
class Solution {
public List<Boolean> findAnswer(int n, int[][] edges) {
List<int[]>[] g = new List[n];
for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(new int[]{e[1], e[2]});
g[e[1]].add(new int[]{e[0], e[2]});
}
long[] d1 = dijkstra(g, 0), d2 = dijkstra(g, n-1);
long shortest = d1[n-1];
List<Boolean> ans = new ArrayList<>();
for (int[] e : edges) {
int u = e[0], v = e[1], w = e[2];
ans.add(d1[u]+w+d2[v]==shortest || d1[v]+w+d2[u]==shortest);
}
return ans;
}
private long[] dijkstra(List<int[]>[] g, int src) {
int n = g.length;
long[] d = new long[n];
Arrays.fill(d, Long.MAX_VALUE);
d[src] = 0;
PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparingLong(a->a[0]));
pq.add(new long[]{0, src});
while (!pq.isEmpty()) {
long[] top = pq.poll();
long du = top[0]; int u = (int)top[1];
if (du > d[u]) continue;
for (int[] vw : g[u]) {
int v = vw[0], w = vw[1];
if (d[v] > d[u]+w) {
d[v] = d[u]+w;
pq.add(new long[]{d[v], v});
}
}
}
return d;
}
}
Kotlin
class Solution {
fun findAnswer(n: Int, edges: Array<IntArray>): List<Boolean> {
val g = Array(n) { mutableListOf<Pair<Int,Int>>() }
for (e in edges) {
g[e[0]].add(e[1] to e[2])
g[e[1]].add(e[0] to e[2])
}
fun dijkstra(src: Int): LongArray {
val d = LongArray(n) { Long.MAX_VALUE }
d[src] = 0L
val pq = java.util.PriorityQueue(compareBy<Pair<Long,Int>> { it.first })
pq.add(0L to src)
while (pq.isNotEmpty()) {
val (du, u) = pq.poll()
if (du > d[u]) continue
for ((v, w) in g[u]) {
if (d[v] > d[u] + w) {
d[v] = d[u] + w
pq.add(d[v] to v)
}
}
}
return d
}
val d1 = dijkstra(0)
val d2 = dijkstra(n-1)
val shortest = d1[n-1]
return edges.map { (u, v, w) ->
d1[u] + w + d2[v] == shortest || d1[v] + w + d2[u] == shortest
}
}
}
Python
class Solution:
def findAnswer(self, n: int, edges: list[list[int]]) -> list[bool]:
from heapq import heappush, heappop
g = [[] for _ in range(n)]
for u, v, w in edges:
g[u].append((v, w))
g[v].append((u, w))
def dijkstra(src: int) -> list[int]:
d = [float('inf')] * n
d[src] = 0
pq = [(0, src)]
while pq:
du, u = heappop(pq)
if du > d[u]: continue
for v, w in g[u]:
if d[v] > d[u] + w:
d[v] = d[u] + w
heappush(pq, (d[v], v))
return d
d1 = dijkstra(0)
d2 = dijkstra(n-1)
shortest = d1[-1]
ans = []
for u, v, w in edges:
ans.append(d1[u] + w + d2[v] == shortest or d1[v] + w + d2[u] == shortest)
return ans
Rust
impl Solution {
pub fn find_answer(n: i32, edges: Vec<Vec<i32>>) -> Vec<bool> {
use std::collections::BinaryHeap;
let n = n as usize;
let mut g = vec![vec![]; n];
for e in &edges {
let (u, v, w) = (e[0] as usize, e[1] as usize, e[2]);
g[u].push((v, w));
g[v].push((u, w));
}
let dijkstra = |src: usize| -> Vec<i64> {
let mut d = vec![i64::MAX; n];
d[src] = 0;
let mut pq = std::collections::BinaryHeap::new();
pq.push((0, src));
while let Some((du, u)) = pq.pop() {
let du = -du;
if du > d[u] { continue; }
for &(v, w) in &g[u] {
let v = v as usize;
let w = w as i64;
if d[v] > d[u] + w {
d[v] = d[u] + w;
pq.push((-d[v], v));
}
}
}
d
};
let d1 = dijkstra(0);
let d2 = dijkstra(n-1);
let shortest = d1[n-1];
edges.iter().map(|e| {
let u = e[0] as usize;
let v = e[1] as usize;
let w = e[2] as i64;
d1[u] + w + d2[v] == shortest || d1[v] + w + d2[u] == shortest
}).collect()
}
}
TypeScript
class Solution {
findAnswer(n: number, edges: number[][]): boolean[] {
const g: [number, number][][] = Array.from({length: n}, () => []);
for (const [u, v, w] of edges) {
g[u].push([v, w]);
g[v].push([u, w]);
}
function dijkstra(src: number): number[] {
const d = Array(n).fill(Infinity);
d[src] = 0;
const pq: [number, number][] = [[0, src]];
while (pq.length) {
pq.sort((a, b) => a[0] - b[0]);
const [du, u] = pq.shift()!;
if (du > d[u]) continue;
for (const [v, w] of g[u]) {
if (d[v] > d[u] + w) {
d[v] = d[u] + w;
pq.push([d[v], v]);
}
}
}
return d;
}
const d1 = dijkstra(0);
const d2 = dijkstra(n-1);
const shortest = d1[n-1];
return edges.map(([u, v, w]) =>
d1[u] + w + d2[v] === shortest || d1[v] + w + d2[u] === shortest
);
}
}
Complexity
- ⏰ Time complexity:
O((n+m)log n), due to Dijkstra's algorithm run twice and edge checks. - 🧺 Space complexity:
O(n+m), for graph and distance arrays.