problemmediumalgorithmsleetcode-802leetcode 802leetcode802

Find Eventual Safe States

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node.

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

Examples

Example 1:

graph LR;
0 --> 1 & 2
1 --> 2 & 3
2 --> 5
3 --> 0
4 --> 5
6

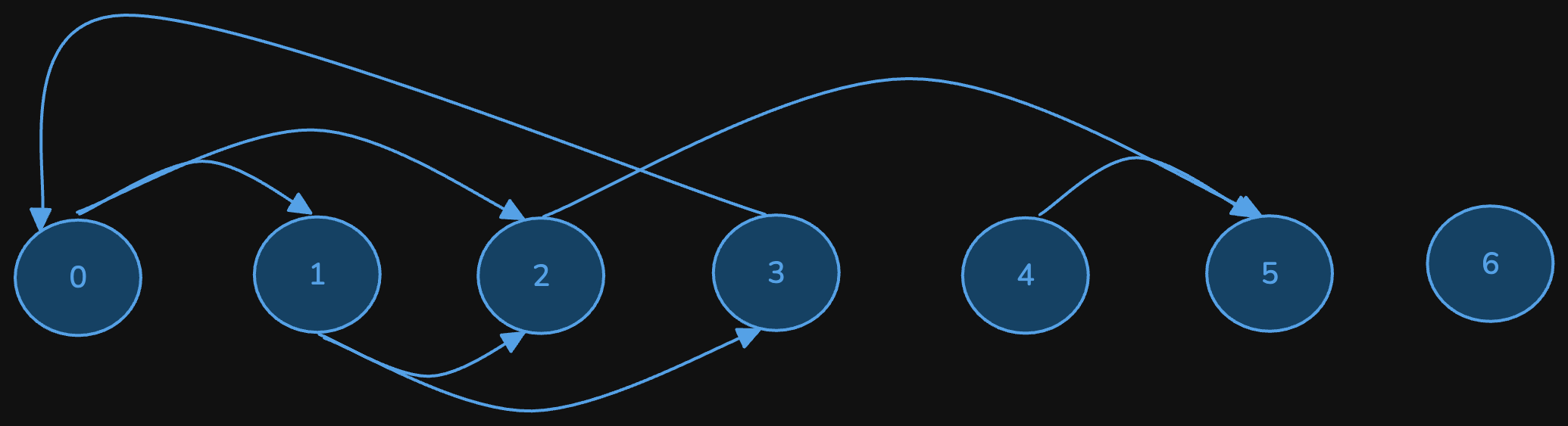
Here is another view of same graph: find-eventual-safe-states-eg1.excalidraw

Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Example 2:

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output:
 [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

So, basically method signature:

public List<Integer> eventualSafeNodes(int[][] graph) {
	
}

Solution

Lets look at example 1. We can see in the graph, that 0 is not a safe node, as that leads to circle. We can go from 0 to 2, and that will eventually lead us to terminal node, but that is just 1 possibility. Likewise, 1 is also not a safe node, as it is part of cycle with node 0. So, basically we need to be careful, not to get in the cycle.

Method 1 - DFS

We are already given adjacency list representation of graph. Lets identify a few nodes:

  1. Terminal Nodes: Nodes with no outgoing edges are terminal nodes and hence safe.
  2. Safe Nodes: A node is considered safe if all possible paths starting from that node only lead to terminal nodes (or other safe nodes).

To identify safe nodes, we can use Depth-First Search (DFS) and track the state of each node:

  • State 0: Node has not been visited.
  • State 1: Node is being visited but not verified as safe (part of the current DFS path).
  • State 2: Node is fully processed and is a safe node.

For every node, follow these checks:

  • If the node is already visited or confirmed to be safe, return its state.
  • If the node has no outgoing edges, mark it as safe by setting its state to 2.
  • For an unvisited node, process each of its outgoing edges by:
    • Recursively running the function on the adjacent nodes.
    • If any adjacent node returns a state of 1 (indicating a cycle), mark the current node as unsafe and return false.
    • If, after processing all adjacent nodes, no cycles are detected, mark the current node as safe by setting its state to 2.

Finally, return the state of the node.

Code

Java
class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int n = graph.length;
        int[] state = new int[n]; // 0: unvisited or unprocessed, 1: visiting, 2: safe
        List<Integer> ans = new ArrayList<>();
        
        for (int i = 0; i < n; i++) {
            if (dfs(i, graph, state)) {
                ans.add(i);
            }
        }
        
        return ans;
    }
    
    private boolean dfs(int node, int[][] graph, int[] state) {
        if (state[node] != 0) {
            return state[node] == 2;
        }
        state[node] = 1;
        for (int nei : graph[node]) {
            if (!dfs(nei, graph, state)) {
                return false;
            }
        }
        state[node] = 2;
        return true;
    }
}
Python
class Solution:
    def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
        n = len(graph)
        state = [0] * n # 0: unvisited, 1: visiting, 2: safe
        ans = []
        
        def dfs(node: int) -> bool:
            if state[node] != 0:
                return state[node] == 2
            state[node] = 1
            for nei in graph[node]:
                if not dfs(nei):
                    return False
            state[node] = 2
            return True
        
        for i in range(n):
            if dfs(i):
                ans.append(i)
        
        return sorted(ans)

Complexity

  • ⏰ Time complexity: O(V + E) where V is the number of nodes and E is the number of edges. Each node and edge is processed a constant number of times.
  • 🧺 Space complexity: O(V) for the recursion stack and the state array used to track the state of each node.

Comments