problemmediumalgorithmsleetcode-658leetcode 658leetcode658

Find K Closest Elements

MediumUpdated: Aug 1, 2025
Practice on:
LeetCode

Problem

Given a sorted integer array arr, two integers k and x, return the k closest integers to x in the array. The result should also be sorted in ascending order.

An integer a is closer to x than an integer b if:

  • |a - x| < |b - x|, or
  • |a - x| == |b - x| and a < b

Examples

Example 1:

Input:
arr = [1,2,3,4,5], k = 4, x = 3
Output:
 [1,2,3,4]

Example 2:

Input:
arr = [1,2,3,4,5], k = 4, x = -1
Output:
 [1,2,3,4]

Solution

Method 1 – Binary Search + Two Pointers

Intuition

Since the array is sorted, we can use binary search to find the position closest to x. Then, we expand outwards using two pointers (left and right) to collect the k closest elements. At each step, we compare which side is closer to x and move the pointer accordingly.

Approach

  1. Use binary search to find the index of the element closest to x.
  2. Initialize two pointers: left = index, right = index + 1.
  3. Expand the window to include k elements:
    • At each step, compare the distance from x to arr[left] and arr[right].
    • Move the pointer (left or right) that is closer to x.
    • If one pointer goes out of bounds, move the other.
  4. Collect the k elements between left+1 and right (inclusive).
  5. Return the result sorted in ascending order (already sorted by construction).

Code

Python
from bisect import bisect_left
from typing import List

class Solution:
	def findClosestElements(self, arr: List[int], k: int, x: int) -> List[int]:
		n = len(arr)
		idx = bisect_left(arr, x)
		left, right = idx - 1, idx
		res = []
		while k > 0:
			if left < 0:
				right += 1
			elif right >= n or abs(arr[left] - x) <= abs(arr[right] - x):
				left -= 1
			else:
				right += 1
			k -= 1
		return arr[left+1:right]
Java
import java.util.*;

class Solution {
	public List<Integer> findClosestElements(int[] arr, int k, int x) {
		int n = arr.length;
		int left = 0, right = n - 1;
		while (right - left >= k) {
			if (Math.abs(arr[left] - x) > Math.abs(arr[right] - x)) {
				left++;
			} else {
				right--;
			}
		}
		List<Integer> res = new ArrayList<>();
		for (int i = left; i <= right; i++) {
			res.add(arr[i]);
		}
		return res;
	}
}
C++
#include <vector>
#include <cmath>
using namespace std;

class Solution {
public:
	vector<int> findClosestElements(vector<int>& arr, int k, int x) {
		int left = 0, right = arr.size() - 1;
		while (right - left >= k) {
			if (abs(arr[left] - x) > abs(arr[right] - x)) {
				left++;
			} else {
				right--;
			}
		}
		return vector<int>(arr.begin() + left, arr.begin() + right + 1);
	}
};
Go
func findClosestElements(arr []int, k int, x int) []int {
	left, right := 0, len(arr)-1
	for right-left >= k {
		if abs(arr[left]-x) > abs(arr[right]-x) {
			left++
		} else {
			right--
		}
	}
	return arr[left : right+1]
}

func abs(a int) int {
	if a < 0 {
		return -a
	}
	return a
}
TypeScript
function findClosestElements(arr: number[], k: number, x: number): number[] {
	let left = 0, right = arr.length - 1;
	while (right - left >= k) {
		if (Math.abs(arr[left] - x) > Math.abs(arr[right] - x)) {
			left++;
		} else {
			right--;
		}
	}
	return arr.slice(left, right + 1);
}

Complexity

  • ⏰ Time complexity: O(n), where n is the length of arr. In the worst case, we scan the array once.
  • 🧺 Space complexity: O(1) (excluding the output list).

src -[6]

it means A[mid + 1] - A[mid + k] is better than A[mid] - A[mid + k - 1], and we have mid smaller than the right i. So assign left = mid + 1.

Method 2 – Binary Search for Window Start (No Math.abs)

Let f[i] = abs(x - arr[i]), where 0 <= i < n. We want to find the starting index startIdx such that the window arr[startIdx...startIdx+k-1] contains the k closest elements to x. Since the array is sorted, we can use binary search to find the leftmost startIdx where the window is optimal.

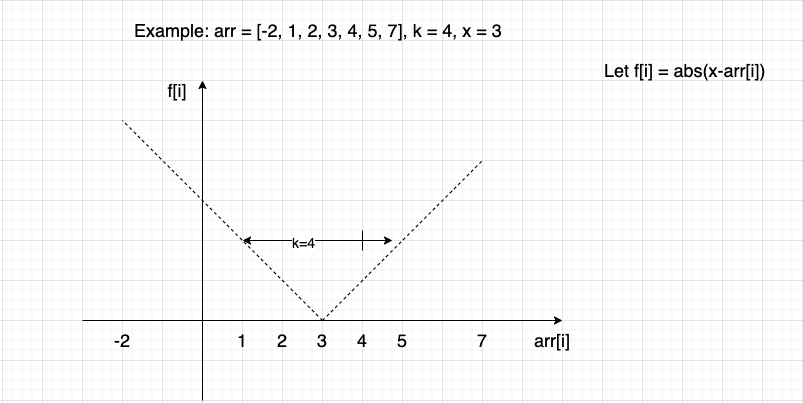
image

Assume we are taking A[i] ~ A[i + k -1]. We binary search for i, and compare the distance between x - A[mid] and A[mid + k] - x:

case 1: x - A[mid] < A[mid + k] - x, need to move window go left
-------x----A[mid]-----------------A[mid + k]----------

case 2: x - A[mid] < A[mid + k] - x, need to move window go left again
-------A[mid]----x-----------------A[mid + k]----------

case 3: x - A[mid] > A[mid + k] - x, need to move window go right
-------A[mid]------------------x---A[mid + k]----------

case 4: x - A[mid] > A[mid + k] - x, need to move window go right
-------A[mid]---------------------A[mid + k]----x------

If x - A[mid] > A[mid + k] - x, it means A[mid + 1] ~ A[mid + k] is a better window than A[mid] ~ A[mid + k - 1], so assign left = mid + 1.

Important

Note: You should not compare the absolute value of abs(x - A[mid]) and abs(A[mid + k] - x). This fails for cases like A = [1,1,2,2,2,2,2,3,3], x = 3, k = 3.

Why We Don't Need Math.abs?

Because the array is already sorted, so the difference is correctly calculated by direct subtraction.

Code

Python
class Solution:
	def findClosestElements(self, arr: list[int], k: int, x: int) -> list[int]:
		left, right = 0, len(arr) - k
		while left < right:
			mid = (left + right) // 2
			if x - arr[mid] > arr[mid + k] - x:
				left = mid + 1
			else:
				right = mid
		return arr[left:left + k]
Java
import java.util.*;

class Solution {
	public List<Integer> findClosestElements(int[] arr, int k, int x) {
		int left = 0, right = arr.length - k;
		while (left < right) {
			int mid = (left + right) / 2;
			if (x - arr[mid] > arr[mid + k] - x) {
				left = mid + 1;
			} else {
				right = mid;
			}
		}
		List<Integer> res = new ArrayList<>();
		for (int i = left; i < left + k; i++) {
			res.add(arr[i]);
		}
		return res;
	}
}
C++
#include <vector>
using namespace std;

class Solution {
public:
	vector<int> findClosestElements(vector<int>& arr, int k, int x) {
		int left = 0, right = arr.size() - k;
		while (left < right) {
			int mid = (left + right) / 2;
			if (x - arr[mid] > arr[mid + k] - x) {
				left = mid + 1;
			} else {
				right = mid;
			}
		}
		return vector<int>(arr.begin() + left, arr.begin() + left + k);
	}
};
Go
func findClosestElements(arr []int, k int, x int) []int {
	left, right := 0, len(arr)-k
	for left < right {
		mid := (left + right) / 2
		if x-arr[mid] > arr[mid+k]-x {
			left = mid + 1
		} else {
			right = mid
		}
	}
	return arr[left : left+k]
}
TypeScript
function findClosestElements(arr: number[], k: number, x: number): number[] {
	let left = 0, right = arr.length - k;
	while (left < right) {
		const mid = Math.floor((left + right) / 2);
		if (x - arr[mid] > arr[mid + k] - x) {
			left = mid + 1;
		} else {
			right = mid;
		}
	}
	return arr.slice(left, left + k);
}

Complexity

  • ⏰ Time complexity: O(log(n - k) + k). Binary search for the window takes O(log(n - k)), and collecting k elements takes O(k).
  • 🧺 Space complexity: O(1) (excluding the output list).

Comments