Find Median from Data Stream

Problem

Given that integers are read from a data stream. Find median of elements read so for in efficient way.

OR

Numbers are randomly generated and passed to a method. Write a program to find and maintain the median value as new values are generated.

OR

You are given a stream of numbers which can be positive or negative. You are required to provide an operation FIND MEDIAN..which when invoked should be able return the median of the numbers in stream(in say O(1) time)

OR

Implement the MedianFinder class:

• MedianFinder() initializes the MedianFinder object.
• void addNum(int num) adds the integer num from the data stream to the data structure.
• double findMedian() returns the median of all elements so far. Answers within 10-5 of the actual answer will be accepted.

OR

Find the rolling median?

Median Definition

[Median Definition](/maths/statistics/median-definition)

Examples

Example 1:

Input:
["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"]
[[], [1], [2], [], [3], []]
Output:
[null, null, null, 1.5, null, 2.0]

Explanation:
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1);    // arr = [1]
medianFinder.addNum(2);    // arr = [1, 2]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3);    // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0

More Examples

For example, median of the stream, nums = [1, 5, 3, 2, 6, 2, 3] is = 3.

Note that we need to find the running median at any time of the stream. That is each time a new number shows up to the stream we need to update the median. For example,

A = [1], median = 1
A = [1,5], median = (5+1)/2 = 3
A = [1,5,3], median = 3
A = [1,5,3,2], median = (2+3)/2 = 2
A = [1,5,3,2,6], median = 3
A = [1,5,3,2,6,2], median = (2+3)/2 = 2
A = [1,5,3,2,6,2,3], median = 3

Observe that at a particular time if there are odd number of elements in then median is the middle element in the sorted order of the stream. That is half of the stream is less than the current median and half of them are greater than the current median. If there are even number of numbers then median is the average of middle two elements such that half of the numbers are less than the median and half of them are greater.

Solution

Video explanation

Here is the video explaining below methods in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/qZkYkIFPYrQ" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Sorting - Sort on Read

Intuition

The most straightforward way to find the median is to have all numbers sorted. If we keep a sorted list of all elements seen so far, the median is simply the middle element(s). There are two main ways to achieve this with sorting.

Approach

1. addNum(num): Simply add the new number to a list. This is an O(1) operation.
2. findMedian(): Sort the entire list (O(N log N)) and then find the middle element(s) (O(1)). This makes finding the median very expensive.

Complexity

• ⏰ Time complexity
  • addNum - O(1)
  • findMedian - O(n log n) due to sorting.
• 🧺 Space complexity: O(n)

Method 2 - Sorting - Keep List Sorted

Intuition

Similar to previous approach.

Approach

1. addNum(num): Insert the new number into the list while maintaining its sorted order. This can be done by finding the correct insertion point (e.g., with a binary search in O(log N)) and then shifting elements to make space (O(N)). The total time is O(N).
2. findMedian(): Since the list is always sorted, we can access the middle element(s) directly in O(1) time.

Complexity

• ⏰ Time complexity: 
  • addNum: O(log n + n) - First binary search and then shifting of elements.
  • findMedian: O(1)
• 🧺 Space complexity: O(n)

Method 3 - Using Self-balancing BST

We can use 2 AVL trees to handle this. For each AVL tree node, track number of nodes within its respective subtree. Utilize an ordinary binary tree node as the root, where its left child constitutes a self-balancing BST holding values smaller than the root, and the right child a self-balancing BST with larger values.

The central root consistently signifies the median value.

If left and right subtrees contain same number of nodes, root node holds average of left and right subtree root data, otherwise, root holds same data as the root of subtree which is having more elements.

After processing an incoming element, the left and right subtrees (BST) are differed utmost by 1.

Self balancing BST is costly in managing balancing factor of BST. However, they provide sorted data which we don’t need. We need median only. Adding the n elements take O(n log n) time, and space complexity is also O(n). Also, rotations will also be costly affair.

Though getting the median takes O(1), as it is at the root of the tree.

Method 4 - Using 2 Heaps (Min and Max heaps) 🏆

Intuition

We don't need the entire list to be sorted to find the median. We only need to efficiently access the elements that would be in the middle if the list were sorted. Two heaps can help us maintain this "middle" section efficiently. We'll keep the smaller half of numbers in one heap (small_nums, a max-heap) and the larger half in another (large_nums, a min-heap), ensuring they are balanced.

Approach

1. We maintain two heaps:
   • small_nums: A max-heap to store the smaller half of the numbers. Its top element will be the largest among the smaller half.
   • large_nums: A min-heap to store the larger half of the numbers. Its top element will be the smallest among the larger half.
2. For addNum(num):
   • Add num to small_nums (max-heap).
   • Move the largest element from small_nums to large_nums (min-heap). This ensures all elements in small_nums are less than or equal to all elements in large_nums.
   • Balance the heaps: Our strategy is to keep small_nums either the same size as large_nums or one element larger. If large_nums ends up with more elements, move the smallest element from large_nums to small_nums.
3. For findMedian():
   • If small_nums has more elements than large_nums (total count is odd), the median is the top element of small_nums.
   • If both heaps have the same number of elements (total count is even), the median is the average of the top elements of small_nums and large_nums.

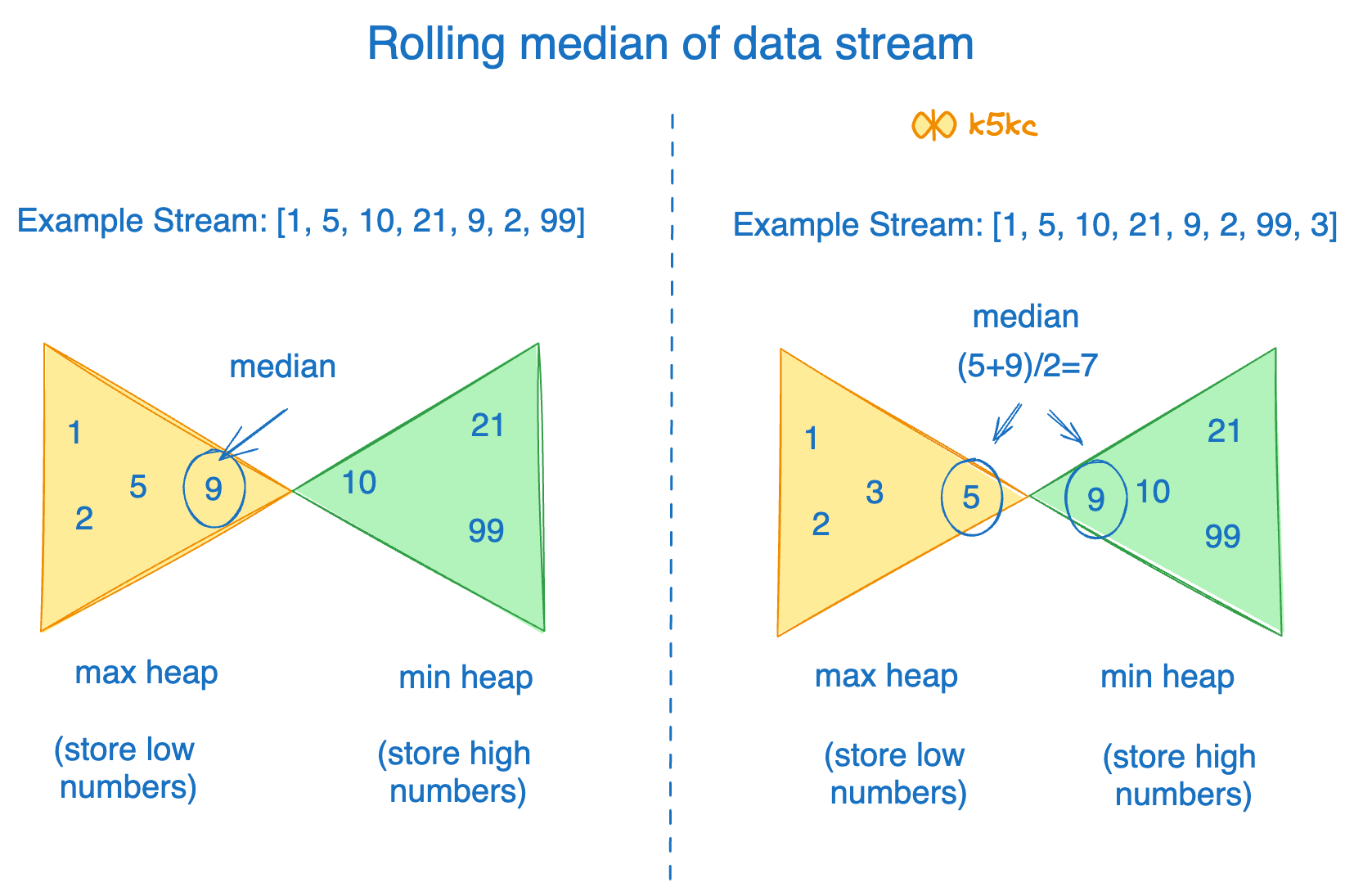
This gives me direct access to the one or two middle values (they're the tops of the heaps), so getting the median takes O(1) time. And adding a number takes O(log n) time.

Code

Java

class MedianFinder {
	private PriorityQueue<Integer> maxHeap; // contains smaller values
	private PriorityQueue<Integer> minHeap; // contains larger value

	public MedianFinder() {
		maxHeap = new PriorityQueue<Integer> (Collections.reverseOrder());
		minHeap = new PriorityQueue<Integer> ();
	}

	// Adds a number into the data structure.
	public void addNum(int num) {
		maxHeap.offer(num);
        minHeap.offer(maxHeap.poll());
		if (minHeap.size() > maxHeap.size())
			maxHeap.offer(minHeap.poll());
		}
	}

	// Returns the median of current data stream
	public double findMedian() {
		if (maxHeap.size() == minHeap.size()) {
			return (double)(maxHeap.peek() + (minHeap.peek())) / 2;
		} else {
			return maxHeap.peek();
		}
	}
}

Complexity

• ⏰ Time complexity
  • addNum - log n due to heap operations
  • findMedian - O(1)
• 🧺 Space complexity: O(n)

Method 5 - Using Skiplist and Queue

See the answer here.

Method 6 - P2 Algorithm

See the answer here.