Find Nearest Right Node in Binary Tree

Problem

Given the root of a binary tree and a node u in the tree, return thenearest node on the same level that is to the right of u , or return null ifu is the rightmost node in its level.

Examples

Example 1:

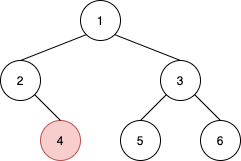
Input: root = [1,2,3,null,4,5,6], u = 4
Output: 5
Explanation: The nearest node on the same level to the right of node 4 is node 5.

Example 2:

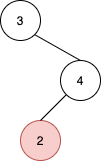
Input: root = [3,null,4,2], u = 2
Output: null
Explanation: There are no nodes to the right of 2.

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 10^5
• All values in the tree are distinct.
• u is a node in the binary tree rooted at root.

Solution

Method 1 – Level Order Traversal (BFS)

Intuition

To find the nearest right node of u on the same level, we can perform a level order traversal (BFS) and, for each level, look for u. If we find u, the next node in the queue (if any) is the answer.

Approach

1. Use a queue to perform BFS, storing nodes level by level.
2. For each level, iterate through all nodes:
   • If the current node is u, return the next node in the queue (if any) for this level.
   • Otherwise, enqueue its children.
3. If u is the rightmost node at its level, return null.

Code

C++

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
};
class Solution {
public:
    TreeNode* findNearestRightNode(TreeNode* root, TreeNode* u) {
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int sz = q.size();
            for (int i = 0; i < sz; ++i) {
                TreeNode* node = q.front(); q.pop();
                if (node == u) return i == sz-1 ? nullptr : q.front();
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        return nullptr;
    }
};

Go

type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}
func findNearestRightNode(root, u *TreeNode) *TreeNode {
    q := []*TreeNode{root}
    for len(q) > 0 {
        sz := len(q)
        for i := 0; i < sz; i++ {
            node := q[0]
            q = q[1:]
            if node == u {
                if i == sz-1 { return nil }
                return q[0]
            }
            if node.Left != nil { q = append(q, node.Left) }
            if node.Right != nil { q = append(q, node.Right) }
        }
    }
    return nil
}

Java

class TreeNode {
    int val;
    TreeNode left, right;
}
class Solution {
    public TreeNode findNearestRightNode(TreeNode root, TreeNode u) {
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                TreeNode node = q.poll();
                if (node == u) return i == sz-1 ? null : q.peek();
                if (node.left != null) q.offer(node.left);
                if (node.right != null) q.offer(node.right);
            }
        }
        return null;
    }
}

Kotlin

data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    fun findNearestRightNode(root: TreeNode?, u: TreeNode?): TreeNode? {
        val q = ArrayDeque<TreeNode?>()
        q.add(root)
        while (q.isNotEmpty()) {
            val sz = q.size
            for (i in 0 until sz) {
                val node = q.removeFirst()
                if (node == u) return if (i == sz-1) null else q.first()
                node?.left?.let { q.add(it) }
                node?.right?.let { q.add(it) }
            }
        }
        return null
    }
}

Python

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def findNearestRightNode(self, root: TreeNode, u: TreeNode) -> TreeNode | None:
        from collections import deque
        q = deque([root])
        while q:
            sz = len(q)
            for i in range(sz):
                node = q.popleft()
                if node == u:
                    return None if i == sz-1 else q[0]
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
        return None

Rust

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn find_nearest_right_node(root: Option<Rc<RefCell<TreeNode>>>, u: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
        use std::collections::VecDeque;
        let mut q = VecDeque::new();
        if let Some(r) = root.clone() { q.push_back(r); }
        while !q.is_empty() {
            let sz = q.len();
            for i in 0..sz {
                let node = q.pop_front().unwrap();
                if Some(node.clone()) == u {
                    return if i == sz-1 { None } else { Some(q.front().unwrap().clone()) };
                }
                let n = node.borrow();
                if let Some(left) = n.left.clone() { q.push_back(left); }
                if let Some(right) = n.right.clone() { q.push_back(right); }
            }
        }
        None
    }
}

TypeScript

class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = val ?? 0;
        this.left = left ?? null;
        this.right = right ?? null;
    }
}
class Solution {
    findNearestRightNode(root: TreeNode | null, u: TreeNode | null): TreeNode | null {
        if (!root || !u) return null;
        const q: (TreeNode | null)[] = [root];
        while (q.length) {
            const sz = q.length;
            for (let i = 0; i < sz; i++) {
                const node = q.shift()!;
                if (node === u) return i === sz-1 ? null : q[0];
                if (node.left) q.push(node.left);
                if (node.right) q.push(node.right);
            }
        }
        return null;
    }
}

Complexity

• ⏰ Time complexity: O(n), where n is the number of nodes in the tree. Each node is visited once.
• 🧺 Space complexity: O(w), where w is the maximum width of the tree (queue size at the largest level).