Find path from root to given node in a binary tree

Problem

Given a binary tree (not a binary search tree), write an algorithm that returns or prints the path from the root to a given target node. The path is represented as a list of node values.

Examples

Example 1

graph TD
    A(1)
    A --- B(2)
    A --- C(3)
    B(2) --- D(4)
    B(2) --- E(5)

    linkStyle 0 stroke:#FF0000,stroke-width:2px;
    linkStyle 3 stroke:#FF0000,stroke-width:2px;

 Input:
 Binary Tree:
         1
        / \
       2   3
      / \
     4   5
 Target Node: 5
 
 Output: [1, 2, 5]
 
 Explanation: The path starts from the root (1), goes to node (2), and ends at the node (5).

Example 2

 Input:
 Binary Tree:
         10
        /  \
       20   30
       /
      40
 Target Node: 40
 
 Output: [10, 20, 40]
 
 Explanation: The path starts from the root (10), goes to node (20), and ends at the node (40).

Example 3

 Input:
 Binary Tree:
         5
        / \
       6   7
 Target Node: 8
 
 Output: []
 
 Explanation: Since the target node (8) is not found in the tree, an empty list is returned.

Similar Problem

[Find distance from root to given node in binary tree](find-distance-from-root-to-given-node-in-binary-tree)

Solution

Method 1 - DFS

To find the path from the root to a given node:

1. Start at the root and check if the current node is the target node.
2. If the node is found, include it in the path and return the path.
3. Otherwise, recursively explore the left and right subtrees.
4. If either the left or right subtree contains the target, append the current node to the path.

This approach ensures we trace the path as we explore the tree. The recursion will stop once the target node is found.

Approach

• Use a recursive function that traverses the tree, starting from the root.
• Pass the path (list) during each recursive call to build the path dynamically.
• Check base cases:
  • If the current node is None, return False.
  • If the current node is the target, append its value to the path and return True.
• Recursively traverse the left and right subtrees until the target node is found.
• If either subtree returns True, append the current node's value to the path.

Dry Run

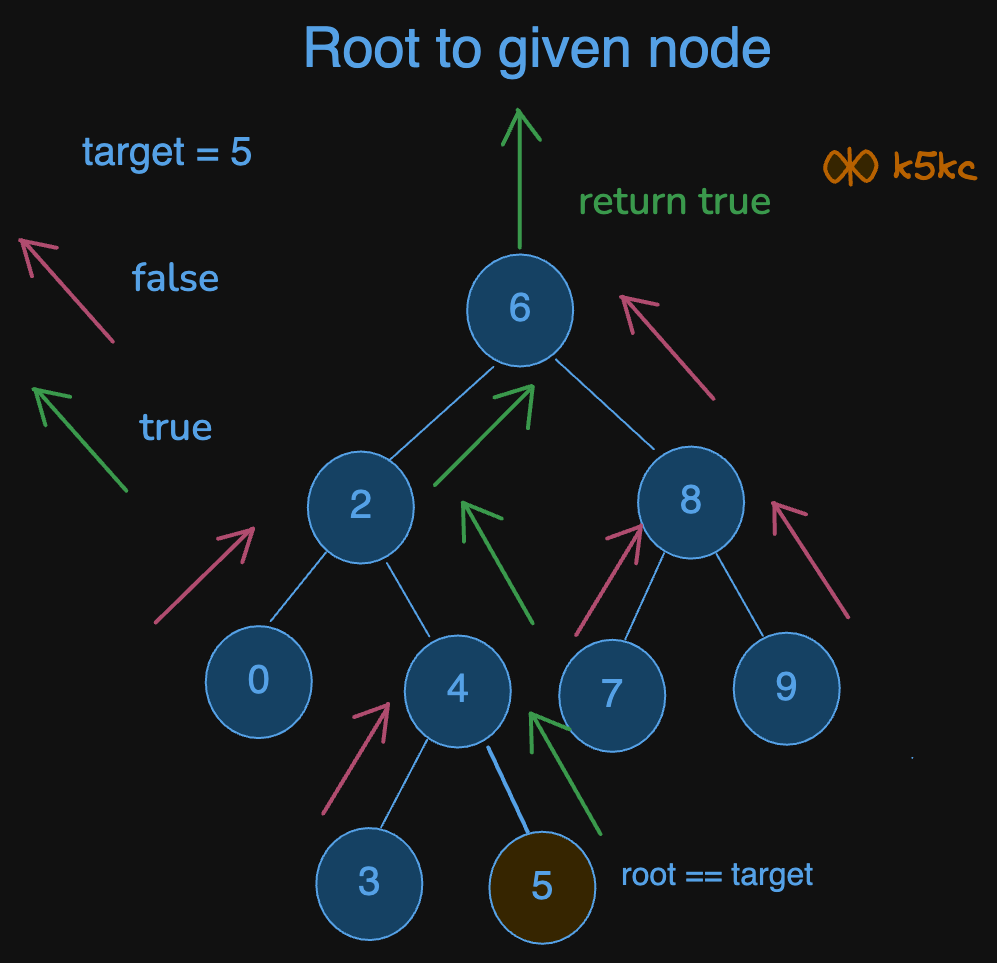
Code

Java

class Solution {
    private List<Integer> path;

    public Solution() {
        this.path = new ArrayList<>();
    }

    public List<Integer> findPath(TreeNode root, int target) {
        path.clear();
        dfs(root, target);
        return path;
    }

    private boolean dfs(TreeNode node, int target) {
        if (node == null) {
            return false;
        }

        // Add the current node to the path
        path.add(node.val);

        // Check if this is the target node
        if (node.val == target) {
            return true;
        }

        // Recursively search in left and right subtrees
        if (dfs(node.left, target) || dfs(node.right, target)) {
            return true;
        }

        // Backtrack if the target is not in this branch
        path.remove(path.size() - 1);
        return false;
    }
}

Python

class Solution:
    def __init__(self):
        self.path = []

    def findPath(self, root, target):
        def dfs(node, target):
            if not node:
                return False
            
            # Append the current node to the path
            self.path.append(node.val)
            
            # Check if this is the target node
            if node.val == target:
                return True
            
            # Recursively search in left and right subtrees
            if dfs(node.left, target) or dfs(node.right, target):
                return True
            
            # Backtrack if the target is not in this branch
            self.path.pop()
            return False

        # Clear the path for each new search
        self.path = []
        dfs(root, target)
        return self.path

Complexity

• ⏰ Time complexity: O(n). We visit each node once in the worst case (if the target node is at the bottom).
• 🧺 Space complexity: O(h). The height of the binary tree due to the recursive call stack, where H is the height of the tree.