problemmediumalgorithmsleetcode-1506leetcode 1506leetcode1506

Find Root of N-Ary Tree

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given all the nodes of an N-ary tree as an array of Node objects, where each node has a unique value.

Return theroot of the N-ary tree.

Custom testing:

An N-ary tree can be serialized as represented in its level order traversal where each group of children is separated by the null value (see examples).

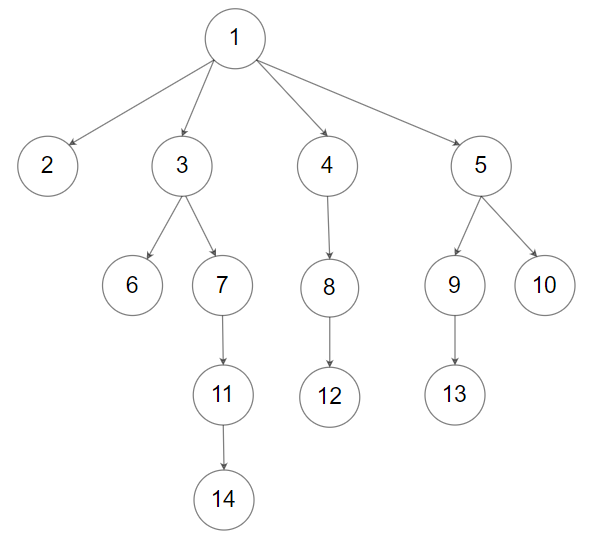
For example, the above tree is serialized as [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14].

The testing will be done in the following way:

  1. The input data should be provided as a serialization of the tree.
  2. The driver code will construct the tree from the serialized input data and put each Node object into an array in an arbitrary order.
  3. The driver code will pass the array to findRoot, and your function should find and return the root Node object in the array.
  4. The driver code will take the returned Node object and serialize it. If the serialized value and the input data are the same , the test passes.

Examples

Example 1:

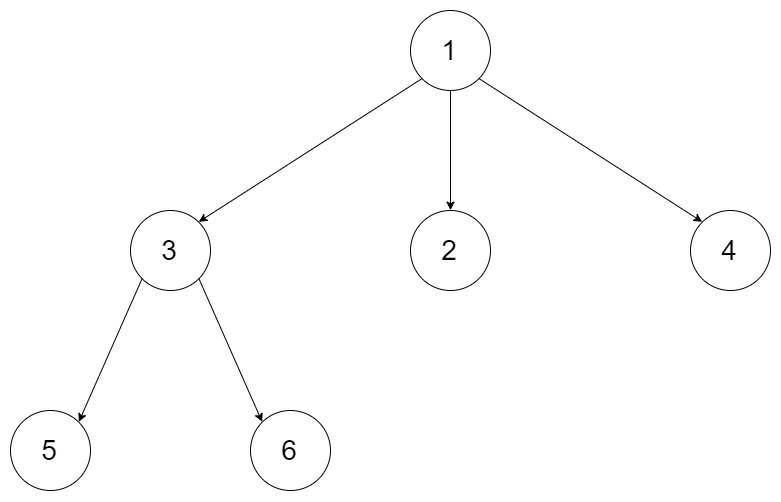
Input: tree = [1,null,3,2,4,null,5,6]
Output: [1,null,3,2,4,null,5,6]
Explanation: The tree from the input data is shown above.
The driver code creates the tree and gives findRoot the Node objects in an arbitrary order.
For example, the passed array could be [Node(5),Node(4),Node(3),Node(6),Node(2),Node(1)] or [Node(2),Node(6),Node(1),Node(3),Node(5),Node(4)].
The findRoot function should return the root Node(1), and the driver code will serialize it and compare with the input data.
The input data and serialized Node(1) are the same, so the test passes.

Example 2:

Input: tree = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

Constraints:

  • The total number of nodes is between [1, 5 * 10^4].
  • Each node has a unique value.

Follow up:

  • Could you solve this problem in constant space complexity with a linear time algorithm?

Solution

Method 1 – Bit Manipulation (XOR All Node Values)

Intuition

Every node except the root appears as a child of some node. If we XOR all node values and all child values, the result will be the root's value, since all other values cancel out.

Approach

  1. Initialize a variable xor_val to 0.
  2. For each node in the list:
    • XOR xor_val with the node's value.
    • For each child, XOR xor_val with the child's value.
  3. After the loop, xor_val will be the value of the root node.
  4. Iterate again to find and return the node with value xor_val.

Code

C++
class Solution {
public:
    Node* findRoot(vector<Node*> tree) {
        int xor_val = 0;
        for (auto node : tree) {
            xor_val ^= node->val;
            for (auto child : node->children) xor_val ^= child->val;
        }
        for (auto node : tree) if (node->val == xor_val) return node;
        return nullptr;
    }
};
Go
func findRoot(tree []*Node) *Node {
    xorVal := 0
    for _, node := range tree {
        xorVal ^= node.Val
        for _, child := range node.Children {
            xorVal ^= child.Val
        }
    }
    for _, node := range tree {
        if node.Val == xorVal {
            return node
        }
    }
    return nil
}
Java
class Solution {
    public Node findRoot(List<Node> tree) {
        int xorVal = 0;
        for (Node node : tree) {
            xorVal ^= node.val;
            for (Node child : node.children) xorVal ^= child.val;
        }
        for (Node node : tree) if (node.val == xorVal) return node;
        return null;
    }
}
Kotlin
class Solution {
    fun findRoot(tree: List<Node>): Node? {
        var xorVal = 0
        for (node in tree) {
            xorVal = xorVal xor node.`val`
            for (child in node.children) xorVal = xorVal xor child.`val`
        }
        return tree.find { it.`val` == xorVal }
    }
}
Python
class Solution:
    def findRoot(self, tree: list['Node']) -> 'Node':
        xor_val = 0
        for node in tree:
            xor_val ^= node.val
            for child in node.children:
                xor_val ^= child.val
        for node in tree:
            if node.val == xor_val:
                return node
        return None
Rust
impl Solution {
    pub fn find_root(tree: Vec<Rc<RefCell<Node>>>) -> Option<Rc<RefCell<Node>>> {
        let mut xor_val = 0;
        for node in &tree {
            let n = node.borrow();
            xor_val ^= n.val;
            for child in &n.children {
                xor_val ^= child.borrow().val;
            }
        }
        for node in &tree {
            if node.borrow().val == xor_val {
                return Some(Rc::clone(node));
            }
        }
        None
    }
}
TypeScript
class Solution {
    findRoot(tree: Node[]): Node | null {
        let xorVal = 0;
        for (const node of tree) {
            xorVal ^= node.val;
            for (const child of node.children) xorVal ^= child.val;
        }
        for (const node of tree) if (node.val === xorVal) return node;
        return null;
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nodes, since we visit each node and child once.
  • 🧺 Space complexity: O(1), since we use only a few variables (excluding input/output).

Comments