Problem

You are given a positive integer n which is the number of nodes of a 0-indexed undirected weighted connected graph and a 0-indexed 2D array edges where edges[i] = [ui, vi, wi] indicates that there is an edge between nodes ui and vi with weight wi.

You are also given two nodes s and d, and a positive integer k, your task is to find the shortest path from s to d, but you can hop over at most k edges. In other words, make the weight of at most k edges 0 and then find the shortest path from s to d.

Return _the length of theshortest path from _s tod with the given condition.

Examples

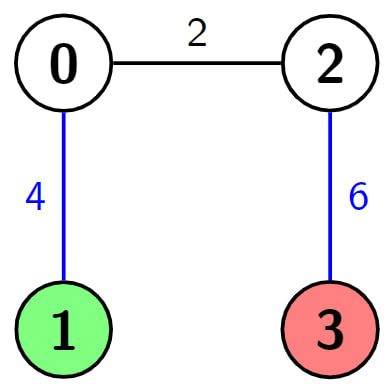
Example 1:

graph TD
    A(0)
    B(1):::greenNode
    C(2)
    D(3):::redNode
    A -- 4 --> B
    A -- 2 --> C
    C -- 6 --> D
    classDef greenNode fill:#43a047,stroke:#333,stroke-width:2;
    classDef redNode fill:#e53935,stroke:#333,stroke-width:2;
  
1
2
3

Input: n = 4, edges = [[0,1,4],[0,2,2],[2,3,6]], s = 1, d = 3, k = 2
Output: 2
Explanation: In this example there is only one path from node 1 (the green node) to node 3 (the red node), which is (1->0->2->3) and the length of it is 4 + 2 + 6 = 12. Now we can make weight of two edges 0, we make weight of the blue edges 0, then we have 0 + 2 + 0 = 2. It can be shown that 2 is the minimum length of a path we can achieve with the given condition.

Example 2:

1
2
3

Input: n = 7, edges = [[3,1,9],[3,2,4],[4,0,9],[0,5,6],[3,6,2],[6,0,4],[1,2,4]], s = 4, d = 1, k = 2
Output: 6
Explanation: In this example there are 2 paths from node 4 (the green node) to node 1 (the red node), which are (4->0->6->3->2->1) and (4->0->6->3->1). The first one has the length 9 + 4 + 2 + 4 + 4 = 23, and the second one has the length 9 + 4 + 2 + 9 = 24. Now if we make weight of the blue edges 0, we get the shortest path with the length 0 + 4 + 2 + 0 = 6. It can be shown that 6 is the minimum length of a path we can achieve with the given condition.


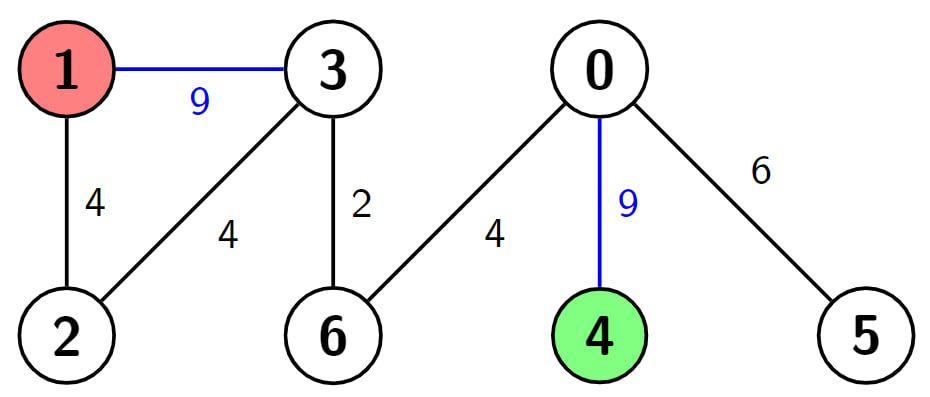
graph TD
    A(0)
    B(1):::redNode
    C(2)
    D(3)
    E(4):::greenNode
    F(5)
    G(6)
    E -- 9 --> A
    A -- 6 --> F
    G -- 4 --> A
    D -- 9 --> B
    D -- 2 --> G
    B -- 4 --> C
    C -- 4 --> D
    classDef greenNode fill:#43a047,stroke:#333,stroke-width:2;
    classDef redNode fill:#e53935,stroke:#333,stroke-width:2;

Example 3:

1
2
3

Input: n = 5, edges = [[0,4,2],[0,1,3],[0,2,1],[2,1,4],[1,3,4],[3,4,7]], s = 2, d = 3, k = 1
Output: 3
Explanation: In this example there are 4 paths from node 2 (the green node) to node 3 (the red node), which are (2->1->3), (2->0->1->3), (2->1->0->4->3) and (2->0->4->3). The first two have the length 4 + 4 = 1 + 3 + 4 = 8, the third one has the length 4 + 3 + 2 + 7 = 16 and the last one has the length 1 + 2 + 7 = 10. Now if we make weight of the blue edge 0, we get the shortest path with the length 1 + 2 + 0 = 3. It can be shown that 3 is the minimum length of a path we can achieve with the given condition.


graph TD
    A(0)
    B(1)
    C(2):::greenNode
    D(3):::redNode
    E(4)
    A -- 2 --> E
    A -- 3 --> B
    A -- 1 --> C
    C -- 4 --> B
    B -- 4 --> D
    E -- 7 --> D
    classDef greenNode fill:#43a047,stroke:#333,stroke-width:2;
    classDef redNode fill:#e53935,stroke:#333,stroke-width:2;

Constraints:

  • 2 <= n <= 500
  • n - 1 <= edges.length <= min(104, n * (n - 1) / 2)
  • edges[i].length = 3
  • 0 <= edges[i][0], edges[i][1] <= n - 1
  • 1 <= edges[i][2] <= 10^6
  • 0 <= s, d, k <= n - 1
  • s != d
  • The input is generated such that the graph is connected and has no repeated edges or self-loops

Solution

Method 1 – Dijkstra with State (Dynamic Programming)

Intuition

To find the shortest path with up to k hops (zero-weight edges), we need to track not only the current node and distance, but also how many hops have been used so far. By extending Dijkstra’s algorithm to include the number of hops as part of the state, we can efficiently find the minimum cost to reach the destination with at most k hops.

Approach

  1. Build the graph as an adjacency list from the edges.
  2. Use a priority queue to perform Dijkstra’s algorithm, where each state is (cost, node, hops_used).
  3. For each node, maintain the minimum cost to reach it with a given number of hops.
  4. When traversing an edge, you can either:
    • Use a hop (set its weight to zero, if you have hops left).
    • Traverse normally (pay the edge weight).
  5. Continue until you reach the destination node, and return the minimum cost among all possible hops used.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
    public int shortestPath(int n, int[][] edges, int s, int d, int k) {
        List<int[]>[] g = new ArrayList[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(new int[]{e[1], e[2]});
            g[e[1]].add(new int[]{e[0], e[2]});
        }
        int[][] dist = new int[n][k + 1];
        for (int[] row : dist) Arrays.fill(row, Integer.MAX_VALUE);
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        dist[s][0] = 0;
        pq.offer(new int[]{0, s, 0});
        while (!pq.isEmpty()) {
            int[] cur = pq.poll();
            int cost = cur[0], u = cur[1], hops = cur[2];
            if (u == d) return cost;
            if (cost > dist[u][hops]) continue;
            for (int[] nei : g[u]) {
                int v = nei[0], w = nei[1];
                // Use a hop
                if (hops < k && cost < dist[v][hops + 1]) {
                    dist[v][hops + 1] = cost;
                    pq.offer(new int[]{cost, v, hops + 1});
                }
                // Normal edge
                if (cost + w < dist[v][hops]) {
                    dist[v][hops] = cost + w;
                    pq.offer(new int[]{cost + w, v, hops});
                }
            }
        }
        return -1;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution:
    def shortestPath(self, n: int, edges: List[List[int]], s: int, d: int, k: int) -> int:
        g = [[] for _ in range(n)]
        for u, v, w in edges:
            g[u].append((v, w))
            g[v].append((u, w))
        dist = [[float('inf')] * (k + 1) for _ in range(n)]
        dist[s][0] = 0
        heap = [(0, s, 0)]
        while heap:
            cost, u, hops = heapq.heappop(heap)
            if u == d:
                return cost
            if cost > dist[u][hops]:
                continue
            for v, w in g[u]:
                # Use a hop
                if hops < k and cost < dist[v][hops + 1]:
                    dist[v][hops + 1] = cost
                    heapq.heappush(heap, (cost, v, hops + 1))
                # Normal edge
                if cost + w < dist[v][hops]:
                    dist[v][hops] = cost + w
                    heapq.heappush(heap, (cost + w, v, hops))
        return -1

Complexity

  • ⏰ Time complexity: O((n + m) * k * log(n * k)) — Each node and hop combination can be visited, and each edge is processed for each hop, with priority queue operations.
  • 🧺 Space complexity: O(n * k) — We store the minimum cost for each node and hop count.