Problem

You are given a 2D matrix grid of size m x n. You are also given a non-negative integer k.

Return the number of submatrices of grid that satisfy the following conditions:

  • The maximum element in the submatrix less than or equal to k.
  • Each row in the submatrix is sorted in non-increasing order.

A submatrix (x1, y1, x2, y2) is a matrix that forms by choosing all cells grid[x][y] where x1 <= x <= x2 and y1 <= y <= y2.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

Input: grid = [[4,3,2,1],[8,7,6,1]], k = 3
Output: 8
Explanation:
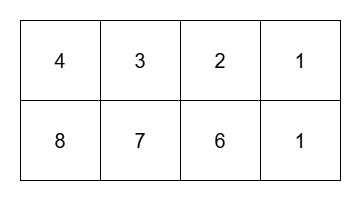**![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/3300-3399/3359.Find%20Sorted%20Submatrices%20With%20Maximum%20Element%20at%20Most%20K/images/mine.png)**
The 8 submatrices are:
* `[[1]]`
* `[[1]]`
* `[[2,1]]`
* `[[3,2,1]]`
* `[[1],[1]]`
* `[[2]]`
* `[[3]]`
* `[[3,2]]`

Example 2:

1
2
3
4
5

Input: grid = [[1,1,1],[1,1,1],[1,1,1]], k = 1
Output: 36
Explanation:
There are 36 submatrices of grid. All submatrices have their maximum element
equal to 1.

Example 3:

1
2

Input: grid = [[1]], k = 1
Output: 1

Constraints:

  • 1 <= m == grid.length <= 10^3
  • 1 <= n == grid[i].length <= 10^3
  • 1 <= grid[i][j] <= 10^9
  • 1 <= k <= 10^9

​​​​​​

Solution

Method 1 – Monotonic Stack and Histogram (Row-wise Processing)

Intuition

For each row, we can use a histogram to represent the number of consecutive rows above (including the current) where each column’s value is at most k and the row is non-increasing. Then, for each row, we count the number of rectangles (submatrices) ending at that row using a monotonic stack, similar to the largest rectangle in histogram problem.

Approach

  1. For each cell, check if the value is at most k and the row is non-increasing up to that column.
  2. Build a height array for each row, where height[j] is the number of consecutive rows above (including current) where the submatrix can extend.
  3. For each row, use a monotonic stack to count the number of rectangles ending at each column.
  4. Sum up the counts for all rows.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    int countSortedSubmatrices(vector<vector<int>>& grid, int k) {
        int m = grid.size(), n = grid[0].size(), ans = 0;
        vector<int> height(n);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] <= k && (j == 0 || grid[i][j] <= grid[i][j-1]))
                    height[j] = height[j] + 1;
                else
                    height[j] = 0;
            }
            stack<int> stk;
            vector<int> left(n);
            for (int j = 0; j < n; ++j) {
                while (!stk.empty() && height[stk.top()] >= height[j]) stk.pop();
                left[j] = j - (stk.empty() ? -1 : stk.top());
                stk.push(j);
            }
            for (int j = 0; j < n; ++j) ans += height[j] * left[j];
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

func countSortedSubmatrices(grid [][]int, k int) int {
    m, n := len(grid), len(grid[0])
    ans := 0
    height := make([]int, n)
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] <= k && (j == 0 || grid[i][j] <= grid[i][j-1]) {
                height[j]++
            } else {
                height[j] = 0
            }
        }
        stk := []int{}
        left := make([]int, n)
        for j := 0; j < n; j++ {
            for len(stk) > 0 && height[stk[len(stk)-1]] >= height[j] {
                stk = stk[:len(stk)-1]
            }
            if len(stk) == 0 {
                left[j] = j + 1
            } else {
                left[j] = j - stk[len(stk)-1]
            }
            stk = append(stk, j)
        }
        for j := 0; j < n; j++ {
            ans += height[j] * left[j]
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
    public int countSortedSubmatrices(int[][] grid, int k) {
        int m = grid.length, n = grid[0].length, ans = 0;
        int[] height = new int[n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] <= k && (j == 0 || grid[i][j] <= grid[i][j-1]))
                    height[j]++;
                else
                    height[j] = 0;
            }
            Deque<Integer> stk = new ArrayDeque<>();
            int[] left = new int[n];
            for (int j = 0; j < n; j++) {
                while (!stk.isEmpty() && height[stk.peek()] >= height[j]) stk.pop();
                left[j] = j - (stk.isEmpty() ? -1 : stk.peek());
                stk.push(j);
            }
            for (int j = 0; j < n; j++) ans += height[j] * left[j];
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    fun countSortedSubmatrices(grid: Array<IntArray>, k: Int): Int {
        val m = grid.size
        val n = grid[0].size
        var ans = 0
        val height = IntArray(n)
        for (i in 0 until m) {
            for (j in 0 until n) {
                if (grid[i][j] <= k && (j == 0 || grid[i][j] <= grid[i][j-1]))
                    height[j]++
                else
                    height[j] = 0
            }
            val stk = ArrayDeque<Int>()
            val left = IntArray(n)
            for (j in 0 until n) {
                while (stk.isNotEmpty() && height[stk.last()] >= height[j]) stk.removeLast()
                left[j] = j - (if (stk.isEmpty()) -1 else stk.last())
                stk.addLast(j)
            }
            for (j in 0 until n) ans += height[j] * left[j]
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
    def countSortedSubmatrices(self, grid: list[list[int]], k: int) -> int:
        m, n = len(grid), len(grid[0])
        ans = 0
        height = [0] * n
        for i in range(m):
            for j in range(n):
                if grid[i][j] <= k and (j == 0 or grid[i][j] <= grid[i][j-1]):
                    height[j] += 1
                else:
                    height[j] = 0
            stk = []
            left = [0] * n
            for j in range(n):
                while stk and height[stk[-1]] >= height[j]:
                    stk.pop()
                left[j] = j - (stk[-1] if stk else -1)
                stk.append(j)
            for j in range(n):
                ans += height[j] * left[j]
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

impl Solution {
    pub fn count_sorted_submatrices(grid: Vec<Vec<i32>>, k: i32) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut ans = 0;
        let mut height = vec![0; n];
        for i in 0..m {
            for j in 0..n {
                if grid[i][j] <= k && (j == 0 || grid[i][j] <= grid[i][j-1]) {
                    height[j] += 1;
                } else {
                    height[j] = 0;
                }
            }
            let mut stk = Vec::new();
            let mut left = vec![0; n];
            for j in 0..n {
                while let Some(&top) = stk.last() {
                    if height[top] >= height[j] { stk.pop(); } else { break; }
                }
                left[j] = j as i32 - if stk.is_empty() { -1 } else { stk[stk.len()-1] as i32 };
                stk.push(j);
            }
            for j in 0..n {
                ans += height[j] * left[j];
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    countSortedSubmatrices(grid: number[][], k: number): number {
        const m = grid.length, n = grid[0].length;
        let ans = 0;
        const height = Array(n).fill(0);
        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                if (grid[i][j] <= k && (j === 0 || grid[i][j] <= grid[i][j-1]))
                    height[j]++;
                else
                    height[j] = 0;
            }
            const stk: number[] = [];
            const left = Array(n).fill(0);
            for (let j = 0; j < n; j++) {
                while (stk.length && height[stk[stk.length-1]] >= height[j]) stk.pop();
                left[j] = j - (stk.length ? stk[stk.length-1] : -1);
                stk.push(j);
            }
            for (let j = 0; j < n; j++) ans += height[j] * left[j];
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(m * n), where m and n are the dimensions of the grid, since each cell is processed a constant number of times.
  • 🧺 Space complexity: O(n), for the height, stack, and left arrays.