Find Subtree Sizes After Changes

Problem

You are given a tree rooted at node 0 that consists of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

We make the following changes on the tree one time simultaneously for all nodes x from 1 to n - 1:

• Find the closest node y to node x such that y is an ancestor of x, and s[x] == s[y].
• If node y does not exist, do nothing.
• Otherwise, remove the edge between x and its current parent and make node y the new parent of x by adding an edge between them.

Return an array answer of size n where answer[i] is the size of the subtree rooted at node i in the final tree.

Examples

Example 1

Input: parent = [-1,0,0,1,1,1], s = "abaabc"

Output: [6,3,1,1,1,1]

Explanation:

![](https://assets.leetcode.com/uploads/2024/08/15/graphex1drawio.png)

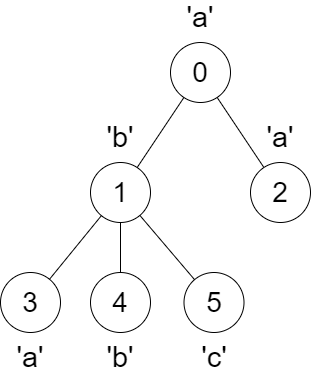
The parent of node 3 will change from node 1 to node 0.

Example 2

Input: parent = [-1,0,4,0,1], s = "abbba"

Output: [5,2,1,1,1]

Explanation:

![](https://assets.leetcode.com/uploads/2024/08/20/exgraph2drawio.png)

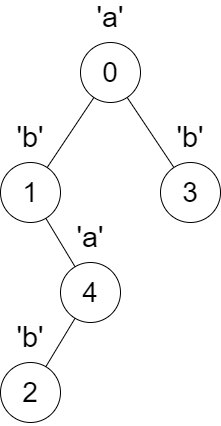
The following changes will happen at the same time:

  * The parent of node 4 will change from node 1 to node 0.
  * The parent of node 2 will change from node 4 to node 1.

Constraints

• n == parent.length == s.length
• 1 <= n <= 10^5
• 0 <= parent[i] <= n - 1 for all i >= 1.
• parent[0] == -1
• parent represents a valid tree.
• s consists only of lowercase English letters.

Solution

Method 1 – DFS with Ancestor Tracking

Intuition

We need to simulate the parent change for each node based on the closest ancestor with the same character. By using DFS and a stack for each character, we can efficiently find the correct ancestor for each node. After updating the parent relationships, we can compute the subtree sizes with another DFS.

Approach

1. Build the initial tree from the parent array.
2. Use DFS to traverse the tree and, for each node, track the closest ancestor with the same character using a stack for each character.
3. For each node (except the root), if a matching ancestor exists, update its parent to that ancestor.
4. Build the new tree with updated parents.
5. Use DFS to compute the size of the subtree rooted at each node in the new tree.
6. Return the subtree sizes.

Code

C++

class Solution {
public:
    vector<int> findSubtreeSizes(vector<int>& parent, string s) {
        int n = parent.size();
        vector<vector<int>> tree(n), newTree(n);
        for (int i = 1; i < n; ++i) tree[parent[i]].push_back(i);
        vector<int> newParent = parent;
        vector<vector<int>> charStack(26);
        function<void(int)> dfs = [&](int u) {
            int c = s[u] - 'a';
            int prev = charStack[c].empty() ? -1 : charStack[c].back();
            charStack[c].push_back(u);
            if (u != 0 && prev != -1) newParent[u] = prev;
            for (int v : tree[u]) dfs(v);
            charStack[c].pop_back();
        };
        dfs(0);
        for (int i = 1; i < n; ++i) newTree[newParent[i]].push_back(i);
        vector<int> ans(n, 1);
        function<void(int)> dfs2 = [&](int u) {
            for (int v : newTree[u]) {
                dfs2(v);
                ans[u] += ans[v];
            }
        };
        dfs2(0);
        return ans;
    }
};

Go

func findSubtreeSizes(parent []int, s string) []int {
    n := len(parent)
    tree := make([][]int, n)
    for i := 1; i < n; i++ {
        tree[parent[i]] = append(tree[parent[i]], i)
    }
    newParent := append([]int{}, parent...)
    charStack := make([][]int, 26)
    var dfs func(int)
    dfs = func(u int) {
        c := int(s[u] - 'a')
        prev := -1
        if len(charStack[c]) > 0 {
            prev = charStack[c][len(charStack[c])-1]
        }
        charStack[c] = append(charStack[c], u)
        if u != 0 && prev != -1 {
            newParent[u] = prev
        }
        for _, v := range tree[u] {
            dfs(v)
        }
        charStack[c] = charStack[c][:len(charStack[c])-1]
    }
    dfs(0)
    newTree := make([][]int, n)
    for i := 1; i < n; i++ {
        newTree[newParent[i]] = append(newTree[newParent[i]], i)
    }
    ans := make([]int, n)
    var dfs2 func(int) int
    dfs2 = func(u int) int {
        ans[u] = 1
        for _, v := range newTree[u] {
            ans[u] += dfs2(v)
        }
        return ans[u]
    }
    dfs2(0)
    return ans
}

Java

class Solution {
    public int[] findSubtreeSizes(int[] parent, String s) {
        int n = parent.length;
        List<Integer>[] tree = new ArrayList[n];
        for (int i = 0; i < n; i++) tree[i] = new ArrayList<>();
        for (int i = 1; i < n; i++) tree[parent[i]].add(i);
        int[] newParent = parent.clone();
        Deque<Integer>[] charStack = new ArrayDeque[26];
        for (int i = 0; i < 26; i++) charStack[i] = new ArrayDeque<>();
        dfs(0, s, tree, charStack, newParent);
        List<Integer>[] newTree = new ArrayList[n];
        for (int i = 0; i < n; i++) newTree[i] = new ArrayList<>();
        for (int i = 1; i < n; i++) newTree[newParent[i]].add(i);
        int[] ans = new int[n];
        dfs2(0, newTree, ans);
        return ans;
    }
    private void dfs(int u, String s, List<Integer>[] tree, Deque<Integer>[] charStack, int[] newParent) {
        int c = s.charAt(u) - 'a';
        Integer prev = charStack[c].peekLast();
        charStack[c].addLast(u);
        if (u != 0 && prev != null) newParent[u] = prev;
        for (int v : tree[u]) dfs(v, s, tree, charStack, newParent);
        charStack[c].removeLast();
    }
    private int dfs2(int u, List<Integer>[] tree, int[] ans) {
        ans[u] = 1;
        for (int v : tree[u]) ans[u] += dfs2(v, tree, ans);
        return ans[u];
    }
}

Kotlin

class Solution {
    fun findSubtreeSizes(parent: IntArray, s: String): IntArray {
        val n = parent.size
        val tree = Array(n) { mutableListOf<Int>() }
        for (i in 1 until n) tree[parent[i]].add(i)
        val newParent = parent.copyOf()
        val charStack = Array(26) { ArrayDeque<Int>() }
        fun dfs(u: Int) {
            val c = s[u] - 'a'
            val prev = charStack[c].lastOrNull()
            charStack[c].addLast(u)
            if (u != 0 && prev != null) newParent[u] = prev
            for (v in tree[u]) dfs(v)
            charStack[c].removeLast()
        }
        dfs(0)
        val newTree = Array(n) { mutableListOf<Int>() }
        for (i in 1 until n) newTree[newParent[i]].add(i)
        val ans = IntArray(n) { 1 }
        fun dfs2(u: Int) {
            for (v in newTree[u]) {
                dfs2(v)
                ans[u] += ans[v]
            }
        }
        dfs2(0)
        return ans
    }
}

Python

class Solution:
    def findSubtreeSizes(self, parent: list[int], s: str) -> list[int]:
        n = len(parent)
        tree = [[] for _ in range(n)]
        for i in range(1, n):
            tree[parent[i]].append(i)
        new_parent = parent[:]
        char_stack = [[] for _ in range(26)]
        def dfs(u: int):
            c = ord(s[u]) - ord('a')
            prev = char_stack[c][-1] if char_stack[c] else -1
            char_stack[c].append(u)
            if u != 0 and prev != -1:
                new_parent[u] = prev
            for v in tree[u]:
                dfs(v)
            char_stack[c].pop()
        dfs(0)
        new_tree = [[] for _ in range(n)]
        for i in range(1, n):
            new_tree[new_parent[i]].append(i)
        ans = [1] * n
        def dfs2(u: int):
            for v in new_tree[u]:
                dfs2(v)
                ans[u] += ans[v]
        dfs2(0)
        return ans

Rust

impl Solution {
    pub fn find_subtree_sizes(parent: Vec<i32>, s: String) -> Vec<i32> {
        let n = parent.len();
        let mut tree = vec![vec![]; n];
        for i in 1..n {
            tree[parent[i] as usize].push(i);
        }
        let mut new_parent = parent.clone();
        let mut char_stack: Vec<Vec<usize>> = vec![vec![]; 26];
        fn dfs(u: usize, s: &[u8], tree: &Vec<Vec<usize>>, char_stack: &mut Vec<Vec<usize>>, new_parent: &mut Vec<i32>) {
            let c = (s[u] - b'a') as usize;
            let prev = *char_stack[c].last().unwrap_or(&usize::MAX);
            char_stack[c].push(u);
            if u != 0 && prev != usize::MAX {
                new_parent[u] = prev as i32;
            }
            for &v in &tree[u] {
                dfs(v, s, tree, char_stack, new_parent);
            }
            char_stack[c].pop();
        }
        dfs(0, s.as_bytes(), &tree, &mut char_stack, &mut new_parent);
        let mut new_tree = vec![vec![]; n];
        for i in 1..n {
            new_tree[new_parent[i] as usize].push(i);
        }
        let mut ans = vec![0; n];
        fn dfs2(u: usize, new_tree: &Vec<Vec<usize>>, ans: &mut Vec<i32>) {
            ans[u] = 1;
            for &v in &new_tree[u] {
                dfs2(v, new_tree, ans);
                ans[u] += ans[v];
            }
        }
        dfs2(0, &new_tree, &mut ans);
        ans
    }
}

TypeScript

class Solution {
    findSubtreeSizes(parent: number[], s: string): number[] {
        const n = parent.length;
        const tree: number[][] = Array.from({ length: n }, () => []);
        for (let i = 1; i < n; ++i) tree[parent[i]].push(i);
        const newParent = parent.slice();
        const charStack: number[][] = Array.from({ length: 26 }, () => []);
        function dfs(u: number) {
            const c = s.charCodeAt(u) - 97;
            const prev = charStack[c].length ? charStack[c][charStack[c].length - 1] : -1;
            charStack[c].push(u);
            if (u !== 0 && prev !== -1) newParent[u] = prev;
            for (const v of tree[u]) dfs(v);
            charStack[c].pop();
        }
        dfs(0);
        const newTree: number[][] = Array.from({ length: n }, () => []);
        for (let i = 1; i < n; ++i) newTree[newParent[i]].push(i);
        const ans = Array(n).fill(1);
        function dfs2(u: number) {
            for (const v of newTree[u]) {
                dfs2(v);
                ans[u] += ans[v];
            }
        }
        dfs2(0);
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n), since each node is visited a constant number of times in both DFS traversals.
• 🧺 Space complexity: O(n), for storing the tree, stacks, and answer arrays.