Find the Closest Marked Node
MediumUpdated: Aug 2, 2025
Practice on:
Problem
You are given a positive integer n which is the number of nodes of a
0-indexed directed weighted graph and a 0-indexed 2D array edges
where edges[i] = [ui, vi, wi] indicates that there is an edge from node ui
to node vi with weight wi.
You are also given a node s and a node array marked; your task is to find the minimum distance from s to any of the nodes in marked.
Return an integer denoting the minimum distance froms to any node inmarked or-1 if there are no paths from s to any of the marked nodes.
Examples
Example 1:
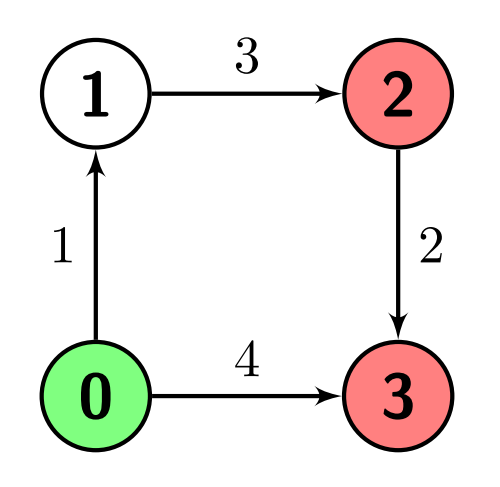
Input: n = 4, edges = [[0,1,1],[1,2,3],[2,3,2],[0,3,4]], s = 0, marked = [2,3]
Output: 4
Explanation: There is one path from node 0 (the green node) to node 2 (a red node), which is 0->1->2, and has a distance of 1 + 3 = 4.
There are two paths from node 0 to node 3 (a red node), which are 0->1->2->3 and 0->3, the first one has a distance of 1 + 3 + 2 = 6 and the second one has a distance of 4.
The minimum of them is 4.
Example 2:
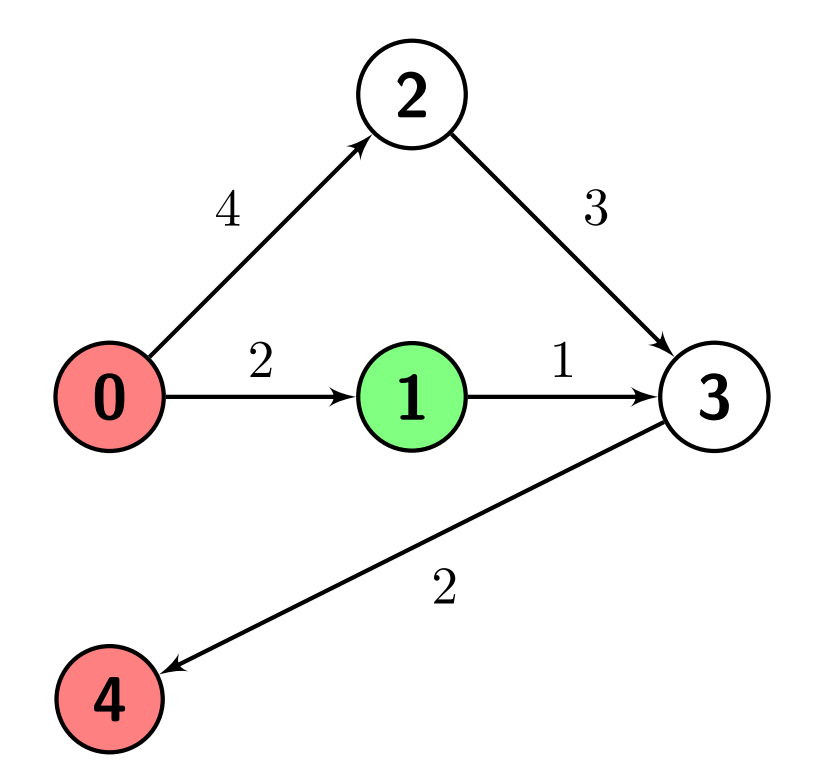
Input: n = 5, edges = [[0,1,2],[0,2,4],[1,3,1],[2,3,3],[3,4,2]], s = 1, marked = [0,4]
Output: 3
Explanation: There are no paths from node 1 (the green node) to node 0 (a red node).
There is one path from node 1 to node 4 (a red node), which is 1->3->4, and has a distance of 1 + 2 = 3.
So the answer is 3.
Example 3:
Input: n = 4, edges = [[0,1,1],[1,2,3],[2,3,2]], s = 3, marked = [0,1]
Output: -1
Explanation: There are no paths from node 3 (the green node) to any of the marked nodes (the red nodes), so the answer is -1.

Constraints:
2 <= n <= 5001 <= edges.length <= 10^4edges[i].length = 30 <= edges[i][0], edges[i][1] <= n - 11 <= edges[i][2] <= 10^61 <= marked.length <= n - 10 <= s, marked[i] <= n - 1s != marked[i]marked[i] != marked[j]for everyi != j- The graph might have repeated edges.
- The graph is generated such that it has no self-loops.
Solution
Method 1 – Dijkstra's Algorithm (Shortest Path)
Intuition
We need the shortest path from the source node s to any node in the marked set. Dijkstra's algorithm is ideal for finding the shortest path in a weighted directed graph with non-negative weights.
Approach
- Build an adjacency list from the edge list.
- Use Dijkstra's algorithm starting from node
sto compute the shortest distance to all nodes. - For each node in
marked, check its distance froms. - Return the minimum distance among all marked nodes, or -1 if none are reachable.
Code
C++
class Solution {
public:
int findClosestMarkedNode(int n, vector<vector<int>>& edges, int s, vector<int>& marked) {
vector<vector<pair<int, int>>> g(n);
for (auto& e : edges) g[e[0]].emplace_back(e[1], e[2]);
vector<long long> dist(n, LLONG_MAX);
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<>> pq;
dist[s] = 0;
pq.emplace(0, s);
while (!pq.empty()) {
auto [d, u] = pq.top(); pq.pop();
if (d > dist[u]) continue;
for (auto& [v, w] : g[u]) {
if (dist[v] > d + w) {
dist[v] = d + w;
pq.emplace(dist[v], v);
}
}
}
long long ans = LLONG_MAX;
for (int v : marked) ans = min(ans, dist[v]);
return ans == LLONG_MAX ? -1 : (int)ans;
}
};
Go
func findClosestMarkedNode(n int, edges [][]int, s int, marked []int) int {
g := make([][]struct{to, w int}, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], struct{to, w int}{e[1], e[2]})
}
dist := make([]int, n)
for i := range dist { dist[i] = 1<<60 }
dist[s] = 0
pq := &heapInt{{0, s}}
heap.Init(pq)
for pq.Len() > 0 {
d, u := (*pq)[0][0], (*pq)[0][1]
heap.Pop(pq)
if d > dist[u] { continue }
for _, e := range g[u] {
if dist[e.to] > d+e.w {
dist[e.to] = d + e.w
heap.Push(pq, [2]int{dist[e.to], e.to})
}
}
}
ans := 1<<60
for _, v := range marked {
if dist[v] < ans { ans = dist[v] }
}
if ans == 1<<60 { return -1 }
return ans
}
// heapInt implements heap.Interface for [2]int
Java
class Solution {
public int findClosestMarkedNode(int n, int[][] edges, int s, int[] marked) {
List<int[]>[] g = new List[n];
for (int i = 0; i < n; ++i) g[i] = new ArrayList<>();
for (int[] e : edges) g[e[0]].add(new int[]{e[1], e[2]});
long[] dist = new long[n];
Arrays.fill(dist, Long.MAX_VALUE);
PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparingLong(a -> a[0]));
dist[s] = 0;
pq.offer(new long[]{0, s});
while (!pq.isEmpty()) {
long[] top = pq.poll();
long d = top[0]; int u = (int)top[1];
if (d > dist[u]) continue;
for (int[] e : g[u]) {
int v = e[0], w = e[1];
if (dist[v] > d + w) {
dist[v] = d + w;
pq.offer(new long[]{dist[v], v});
}
}
}
long ans = Long.MAX_VALUE;
for (int v : marked) ans = Math.min(ans, dist[v]);
return ans == Long.MAX_VALUE ? -1 : (int)ans;
}
}
Kotlin
class Solution {
fun findClosestMarkedNode(n: Int, edges: Array<IntArray>, s: Int, marked: IntArray): Int {
val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
for (e in edges) g[e[0]].add(e[1] to e[2])
val dist = LongArray(n) { Long.MAX_VALUE }
val pq = java.util.PriorityQueue(compareBy<Pair<Long, Int>> { it.first })
dist[s] = 0L
pq.add(0L to s)
while (pq.isNotEmpty()) {
val (d, u) = pq.poll()
if (d > dist[u]) continue
for ((v, w) in g[u]) {
if (dist[v] > d + w) {
dist[v] = d + w
pq.add(dist[v] to v)
}
}
}
var ans = Long.MAX_VALUE
for (v in marked) ans = minOf(ans, dist[v])
return if (ans == Long.MAX_VALUE) -1 else ans.toInt()
}
}
Python
import heapq
class Solution:
def findClosestMarkedNode(self, n: int, edges: list[list[int]], s: int, marked: list[int]) -> int:
g = [[] for _ in range(n)]
for u, v, w in edges:
g[u].append((v, w))
dist = [float('inf')] * n
dist[s] = 0
h = [(0, s)]
while h:
d, u = heapq.heappop(h)
if d > dist[u]: continue
for v, w in g[u]:
if dist[v] > d + w:
dist[v] = d + w
heapq.heappush(h, (dist[v], v))
ans = min((dist[v] for v in marked), default=float('inf'))
return -1 if ans == float('inf') else ans
Rust
use std::collections::BinaryHeap;
use std::cmp::Reverse;
impl Solution {
pub fn find_closest_marked_node(n: i32, edges: Vec<Vec<i32>>, s: i32, marked: Vec<i32>) -> i32 {
let n = n as usize;
let mut g = vec![vec![]; n];
for e in &edges {
g[e[0] as usize].push((e[1] as usize, e[2] as i64));
}
let mut dist = vec![i64::MAX; n];
let mut heap = BinaryHeap::new();
dist[s as usize] = 0;
heap.push(Reverse((0, s as usize)));
while let Some(Reverse((d, u))) = heap.pop() {
if d > dist[u] { continue; }
for &(v, w) in &g[u] {
if dist[v] > d + w {
dist[v] = d + w;
heap.push(Reverse((dist[v], v)));
}
}
}
let mut ans = i64::MAX;
for &v in &marked {
ans = ans.min(dist[v as usize]);
}
if ans == i64::MAX { -1 } else { ans as i32 }
}
}
TypeScript
class Solution {
findClosestMarkedNode(n: number, edges: number[][], s: number, marked: number[]): number {
const g: [number, number][][] = Array.from({length: n}, () => []);
for (const [u, v, w] of edges) g[u].push([v, w]);
const dist = Array(n).fill(Infinity);
dist[s] = 0;
const h: [number, number][] = [[0, s]];
while (h.length) {
h.sort((a, b) => a[0] - b[0]);
const [d, u] = h.shift()!;
if (d > dist[u]) continue;
for (const [v, w] of g[u]) {
if (dist[v] > d + w) {
dist[v] = d + w;
h.push([dist[v], v]);
}
}
}
let ans = Infinity;
for (const v of marked) ans = Math.min(ans, dist[v]);
return ans === Infinity ? -1 : ans;
}
}
Complexity
- ⏰ Time complexity:
O((n + m) log n), where n is the number of nodes and m is the number of edges, due to Dijkstra's algorithm. - 🧺 Space complexity:
O(n + m), for the adjacency list and distance array.