Find the Grid of Region Average

Problem

You are given m x n grid image which represents a grayscale image, where image[i][j] represents a pixel with intensity in the range [0..255]. You are also given a non-negative integer threshold.

Two pixels are adjacent if they share an edge.

A region is a 3 x 3 subgrid where the absolute difference in intensity between any two adjacent pixels is less than or equal to threshold.

All pixels in a region belong to that region, note that a pixel can belong to multiple regions.

You need to calculate a m x n grid result, where result[i][j] is the average intensity of the regions to which image[i][j] belongs, rounded down to the nearest integer. If image[i][j] belongs to multiple regions, result[i][j] is the average of therounded-down average intensities of these regions, rounded down to the nearest integer. If image[i][j] doesnot belong to any region, result[i][j] is equal to image[i][j].

Return the grid result.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18



Input: image = [[5,6,7,10],[8,9,10,10],[11,12,13,10]], threshold = 3

Output: [[9,9,9,9],[9,9,9,9],[9,9,9,9]]

Explanation:

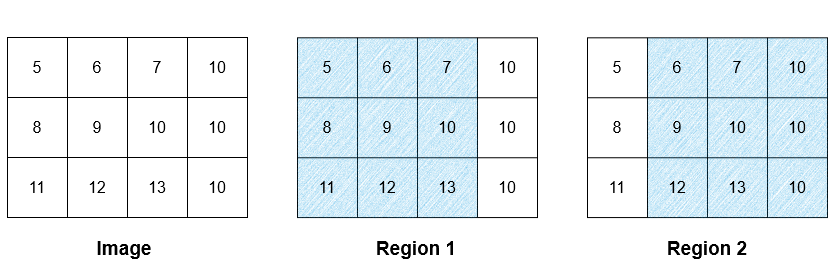
![](https://assets.leetcode.com/uploads/2023/12/21/example0corrected.png)

There are two regions as illustrated above. The average intensity of the first
region is 9, while the average intensity of the second region is 9.67 which is
rounded down to 9. The average intensity of both of the regions is (9 + 9) / 2
= 9. As all the pixels belong to either region 1, region 2, or both of them,
the intensity of every pixel in the result is 9.

Please note that the rounded-down values are used when calculating the average
of multiple regions, hence the calculation is done using 9 as the average
intensity of region 2, not 9.67.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19



Input: image = [[10,20,30],[15,25,35],[20,30,40],[25,35,45]], threshold =
12

Output: [[25,25,25],[27,27,27],[27,27,27],[30,30,30]]

Explanation:

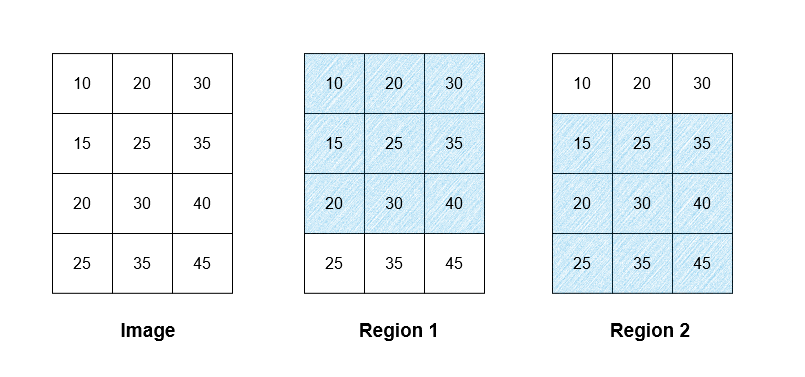
![](https://assets.leetcode.com/uploads/2023/12/21/example1corrected.png)

There are two regions as illustrated above. The average intensity of the first
region is 25, while the average intensity of the second region is 30. The
average intensity of both of the regions is (25 + 30) / 2 = 27.5 which is
rounded down to 27.

All the pixels in row 0 of the image belong to region 1, hence all the pixels
in row 0 in the result are 25. Similarly, all the pixels in row 3 in the
result are 30. The pixels in rows 1 and 2 of the image belong to region 1 and
region 2, hence their assigned value is 27 in the result.

Example 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11



Input: image = [[5,6,7],[8,9,10],[11,12,13]], threshold = 1

Output: [[5,6,7],[8,9,10],[11,12,13]]

Explanation:

There is only one `3 x 3` subgrid, while it does not have the condition on
difference of adjacent pixels, for example, the difference between
`image[0][0]` and `image[1][0]` is `|5 - 8| = 3 > threshold = 1`. None of them
belong to any valid regions, so the `result` should be the same as `image`.

Constraints

3 <= n, m <= 500
0 <= image[i][j] <= 255
0 <= threshold <= 255

Solution

Method 1 – Sliding Window and Region Validation

Intuition

For each possible 3x3 region, check if all adjacent pixels have an absolute difference ≤ threshold. If valid, compute the region’s average and assign it to all pixels in the region. For each pixel, average the values of all regions it belongs to. If a pixel belongs to no region, its value remains unchanged.

Approach

For each possible 3x3 region (top-left at (i, j)), check all adjacent pairs for the threshold condition.
If valid, compute the region’s average (sum of 9 pixels // 9).
For each pixel in the region, keep a list of region averages it belongs to.
For each pixel, if it belongs to at least one region, set result[i][j] to the average of its region averages (rounded down). Otherwise, set result[i][j] = image[i][j].

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


class Solution {
public:
    vector<vector<int>> resultGrid(vector<vector<int>>& image, int threshold) {
        int m = image.size(), n = image[0].size();
        vector<vector<vector<int>>> regions(m, vector<vector<int>>(n));
        vector<pair<int, int>> dirs = {{0,1},{1,0}};
        for (int i = 0; i + 2 < m; ++i) {
            for (int j = 0; j + 2 < n; ++j) {
                bool valid = true;
                for (int x = 0; x < 3 && valid; ++x) {
                    for (int y = 0; y < 3 && valid; ++y) {
                        for (auto& d : dirs) {
                            int ni = i + x + d.first, nj = j + y + d.second;
                            if (ni < i || ni > i+2 || nj < j || nj > j+2) continue;
                            if (abs(image[i+x][j+y] - image[ni][nj]) > threshold) {
                                valid = false;
                                break;
                            }
                        }
                    }
                }
                if (valid) {
                    int sum = 0;
                    for (int x = 0; x < 3; ++x)
                        for (int y = 0; y < 3; ++y)
                            sum += image[i+x][j+y];
                    int avg = sum / 9;
                    for (int x = 0; x < 3; ++x)
                        for (int y = 0; y < 3; ++y)
                            regions[i+x][j+y].push_back(avg);
                }
            }
        }
        vector<vector<int>> res(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (!regions[i][j].empty()) {
                    int s = 0;
                    for (int v : regions[i][j]) s += v;
                    res[i][j] = s / regions[i][j].size();
                } else {
                    res[i][j] = image[i][j];
                }
            }
        }
        return res;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58


func resultGrid(image [][]int, threshold int) [][]int {
    m, n := len(image), len(image[0])
    regions := make([][][]int, m)
    for i := range regions {
        regions[i] = make([][]int, n)
    }
    dirs := [][2]int{{0,1},{1,0}}
    for i := 0; i+2 < m; i++ {
        for j := 0; j+2 < n; j++ {
            valid := true
            for x := 0; x < 3 && valid; x++ {
                for y := 0; y < 3 && valid; y++ {
                    for _, d := range dirs {
                        ni, nj := i+x+d[0], j+y+d[1]
                        if ni < i || ni > i+2 || nj < j || nj > j+2 {
                            continue
                        }
                        if abs(image[i+x][j+y]-image[ni][nj]) > threshold {
                            valid = false
                            break
                        }
                    }
                }
            }
            if valid {
                sum := 0
                for x := 0; x < 3; x++ {
                    for y := 0; y < 3; y++ {
                        sum += image[i+x][j+y]
                    }
                }
                avg := sum / 9
                for x := 0; x < 3; x++ {
                    for y := 0; y < 3; y++ {
                        regions[i+x][j+y] = append(regions[i+x][j+y], avg)
                    }
                }
            }
        }
    }
    res := make([][]int, m)
    for i := range res {
        res[i] = make([]int, n)
        for j := 0; j < n; j++ {
            if len(regions[i][j]) > 0 {
                s := 0
                for _, v := range regions[i][j] {
                    s += v
                }
                res[i][j] = s / len(regions[i][j])
            } else {
                res[i][j] = image[i][j]
            }
        }
    }
    return res
}
func abs(a int) int { if a < 0 { return -a }; return a }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46


class Solution {
    public int[][] resultGrid(int[][] image, int threshold) {
        int m = image.length, n = image[0].length;
        List<Integer>[][] regions = new ArrayList[m][n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                regions[i][j] = new ArrayList<>();
        int[][] dirs = {{0,1},{1,0}};
        for (int i = 0; i + 2 < m; ++i) {
            for (int j = 0; j + 2 < n; ++j) {
                boolean valid = true;
                for (int x = 0; x < 3 && valid; ++x)
                    for (int y = 0; y < 3 && valid; ++y)
                        for (int[] d : dirs) {
                            int ni = i + x + d[0], nj = j + y + d[1];
                            if (ni < i || ni > i+2 || nj < j || nj > j+2) continue;
                            if (Math.abs(image[i+x][j+y] - image[ni][nj]) > threshold) {
                                valid = false;
                                break;
                            }
                        }
                if (valid) {
                    int sum = 0;
                    for (int x = 0; x < 3; ++x)
                        for (int y = 0; y < 3; ++y)
                            sum += image[i+x][j+y];
                    int avg = sum / 9;
                    for (int x = 0; x < 3; ++x)
                        for (int y = 0; y < 3; ++y)
                            regions[i+x][j+y].add(avg);
                }
            }
        }
        int[][] res = new int[m][n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (!regions[i][j].isEmpty()) {
                    int s = 0;
                    for (int v : regions[i][j]) s += v;
                    res[i][j] = s / regions[i][j].size();
                } else {
                    res[i][j] = image[i][j];
                }
        return res;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


class Solution {
    fun resultGrid(image: Array<IntArray>, threshold: Int): Array<IntArray> {
        val m = image.size
        val n = image[0].size
        val regions = Array(m) { Array(n) { mutableListOf<Int>() } }
        val dirs = arrayOf(intArrayOf(0,1), intArrayOf(1,0))
        for (i in 0..m-3) {
            for (j in 0..n-3) {
                var valid = true
                for (x in 0..2) for (y in 0..2) for (d in dirs) {
                    val ni = i + x + d[0]
                    val nj = j + y + d[1]
                    if (ni < i || ni > i+2 || nj < j || nj > j+2) continue
                    if (kotlin.math.abs(image[i+x][j+y] - image[ni][nj]) > threshold) {
                        valid = false
                        break
                    }
                }
                if (valid) {
                    var sum = 0
                    for (x in 0..2) for (y in 0..2) sum += image[i+x][j+y]
                    val avg = sum / 9
                    for (x in 0..2) for (y in 0..2) regions[i+x][j+y].add(avg)
                }
            }
        }
        val res = Array(m) { IntArray(n) }
        for (i in 0 until m) for (j in 0 until n)
            res[i][j] = if (regions[i][j].isNotEmpty()) regions[i][j].sum() / regions[i][j].size else image[i][j]
        return res
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


class Solution:
    def resultGrid(self, image: list[list[int]], threshold: int) -> list[list[int]]:
        m, n = len(image), len(image[0])
        regions = [[[] for _ in range(n)] for _ in range(m)]
        dirs = [(0,1),(1,0)]
        for i in range(m-2):
            for j in range(n-2):
                valid = True
                for x in range(3):
                    for y in range(3):
                        for dx, dy in dirs:
                            ni, nj = i+x+dx, j+y+dy
                            if ni < i or ni > i+2 or nj < j or nj > j+2:
                                continue
                            if abs(image[i+x][j+y] - image[ni][nj]) > threshold:
                                valid = False
                                break
                        if not valid:
                            break
                    if not valid:
                        break
                if valid:
                    s = sum(image[i+x][j+y] for x in range(3) for y in range(3))
                    avg = s // 9
                    for x in range(3):
                        for y in range(3):
                            regions[i+x][j+y].append(avg)
        res = [[0]*n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if regions[i][j]:
                    res[i][j] = sum(regions[i][j]) // len(regions[i][j])
                else:
                    res[i][j] = image[i][j]
        return res

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52


impl Solution {
    pub fn result_grid(image: Vec<Vec<i32>>, threshold: i32) -> Vec<Vec<i32>> {
        let m = image.len();
        let n = image[0].len();
        let mut regions = vec![vec![vec![]; n]; m];
        let dirs = [(0,1),(1,0)];
        for i in 0..m-2 {
            for j in 0..n-2 {
                let mut valid = true;
                'outer: for x in 0..3 {
                    for y in 0..3 {
                        for &(dx,dy) in &dirs {
                            let ni = i+x+dx;
                            let nj = j+y+dy;
                            if ni < i || ni > i+2 || nj < j || nj > j+2 { continue; }
                            if (image[i+x][j+y] - image[ni][nj]).abs() > threshold {
                                valid = false;
                                break 'outer;
                            }
                        }
                    }
                }
                if valid {
                    let mut sum = 0;
                    for x in 0..3 {
                        for y in 0..3 {
                            sum += image[i+x][j+y];
                        }
                    }
                    let avg = sum / 9;
                    for x in 0..3 {
                        for y in 0..3 {
                            regions[i+x][j+y].push(avg);
                        }
                    }
                }
            }
        }
        let mut res = vec![vec![0; n]; m];
        for i in 0..m {
            for j in 0..n {
                if !regions[i][j].is_empty() {
                    let s: i32 = regions[i][j].iter().sum();
                    res[i][j] = s / regions[i][j].len() as i32;
                } else {
                    res[i][j] = image[i][j];
                }
            }
        }
        res
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


class Solution {
    resultGrid(image: number[][], threshold: number): number[][] {
        const m = image.length, n = image[0].length;
        const regions: number[][][] = Array.from({length: m}, () => Array.from({length: n}, () => []));
        const dirs = [[0,1],[1,0]];
        for (let i = 0; i+2 < m; ++i) {
            for (let j = 0; j+2 < n; ++j) {
                let valid = true;
                for (let x = 0; x < 3 && valid; ++x) {
                    for (let y = 0; y < 3 && valid; ++y) {
                        for (const [dx,dy] of dirs) {
                            const ni = i+x+dx, nj = j+y+dy;
                            if (ni < i || ni > i+2 || nj < j || nj > j+2) continue;
                            if (Math.abs(image[i+x][j+y] - image[ni][nj]) > threshold) {
                                valid = false;
                                break;
                            }
                        }
                    }
                }
                if (valid) {
                    let sum = 0;
                    for (let x = 0; x < 3; ++x)
                        for (let y = 0; y < 3; ++y)
                            sum += image[i+x][j+y];
                    const avg = Math.floor(sum / 9);
                    for (let x = 0; x < 3; ++x)
                        for (let y = 0; y < 3; ++y)
                            regions[i+x][j+y].push(avg);
                }
            }
        }
        const res: number[][] = Array.from({length: m}, () => Array(n).fill(0));
        for (let i = 0; i < m; ++i)
            for (let j = 0; j < n; ++j)
                res[i][j] = regions[i][j].length ? Math.floor(regions[i][j].reduce((a,b)=>a+b,0) / regions[i][j].length) : image[i][j];
        return res;
    }
}

Complexity

⏰ Time complexity: O(m * n), as each 3x3 region and each pixel is processed a constant number of times.
🧺 Space complexity: O(m * n), for storing region lists and the result grid.

Problem#

Examples#

Example 1#

Example 2#

Example 3#

Constraints#

Solution#

Method 1 – Sliding Window and Region Validation#

Intuition#

Approach#

Code#

Complexity#