Find the Largest Area of Square Inside Two Rectangles

Problem

There exist n rectangles in a 2D plane with edges parallel to the x and y axis. You are given two 2D integer arrays bottomLeft and topRight where bottomLeft[i] = [a_i, b_i] and topRight[i] = [c_i, d_i] represent the bottom-left and top-right coordinates of the ith rectangle, respectively.

You need to find the maximum area of a square that can fit inside the intersecting region of at least two rectangles. Return 0 if such a square does not exist.

Examples

Example 1

![](https://assets.leetcode.com/uploads/2024/01/05/example12.png)

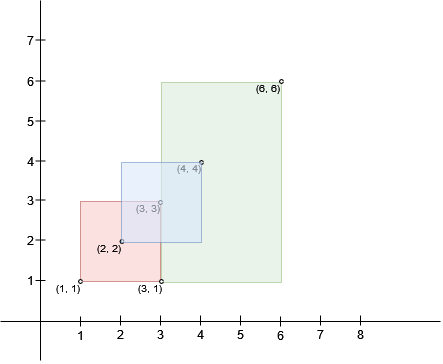
Input: bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]

Output: 1

Explanation:

A square with side length 1 can fit inside either the intersecting region of
rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the
maximum area is 1. It can be shown that a square with a greater side length
can not fit inside any intersecting region of two rectangles.

Example 2

![](https://assets.leetcode.com/uploads/2024/07/15/diag.png)

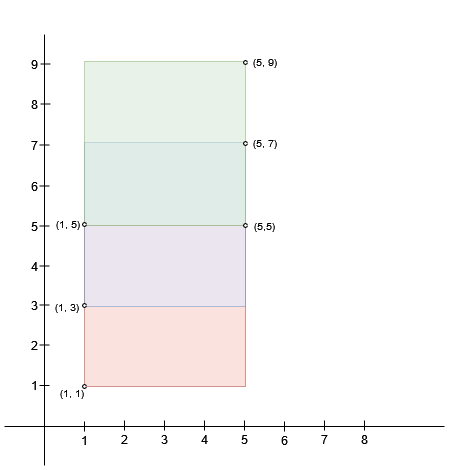
Input: bottomLeft = [[1,1],[1,3],[1,5]], topRight = [[5,5],[5,7],[5,9]]

Output: 4

Explanation:

A square with side length 2 can fit inside either the intersecting region of
rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the
maximum area is `2 * 2 = 4`. It can be shown that a square with a greater side
length can not fit inside any intersecting region of two rectangles.

Example 3

` ![](https://assets.leetcode.com/uploads/2024/01/04/rectanglesexample2.png) `

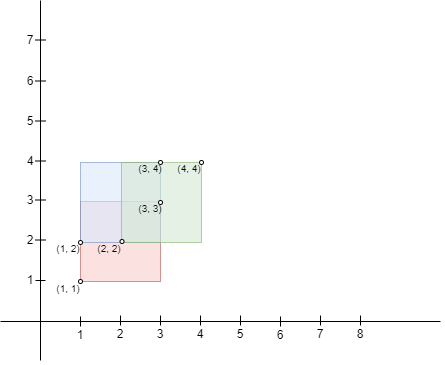Input: bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]

Output: 1

Explanation:

A square with side length 1 can fit inside the intersecting region of any two
rectangles. Also, no larger square can, so the maximum area is 1. Note that
the region can be formed by the intersection of more than 2 rectangles.

#### Example 4

` ![](https://assets.leetcode.com/uploads/2024/01/04/rectanglesexample3.png) `

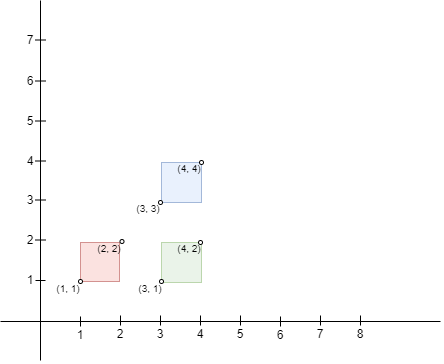**Input:  **bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]

Output: 0

Explanation:

No pair of rectangles intersect, hence, the answer is 0.

Constraints

• n == bottomLeft.length == topRight.length
• 2 <= n <= 10^3
• bottomLeft[i].length == topRight[i].length == 2
• 1 <= bottomLeft[i][0], bottomLeft[i][1] <= 10^7
• 1 <= topRight[i][0], topRight[i][1] <= 10^7
• bottomLeft[i][0] < topRight[i][0]
• bottomLeft[i][1] < topRight[i][1]

Solution

Method 1 – Pairwise Rectangle Intersection + Greedy Square Fitting

Intuition

The largest square that can fit inside the intersection of two rectangles is determined by the width and height of their overlapping region. For each pair of rectangles, compute their intersection, and check the largest square that fits. The answer is the maximum such square area among all pairs.

Approach

1. For every pair of rectangles:
   • Compute the intersection region (if any) by taking the max of bottom-lefts and min of top-rights.
   • If the intersection is valid (width > 0 and height > 0), the largest square that fits has side = min(width, height).
2. Track the maximum square area found among all pairs.
3. Return 0 if no intersection exists for any pair.

Code

C++

class Solution {
public:
    int largestSquareArea(vector<vector<int>>& bottomLeft, vector<vector<int>>& topRight) {
        int n = bottomLeft.size(), ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                int x1 = max(bottomLeft[i][0], bottomLeft[j][0]);
                int y1 = max(bottomLeft[i][1], bottomLeft[j][1]);
                int x2 = min(topRight[i][0], topRight[j][0]);
                int y2 = min(topRight[i][1], topRight[j][1]);
                int w = x2 - x1, h = y2 - y1;
                if (w > 0 && h > 0) ans = max(ans, min(w, h) * min(w, h));
            }
        }
        return ans;
    }
};

Go

func largestSquareArea(bottomLeft [][]int, topRight [][]int) int {
    n, ans := len(bottomLeft), 0
    for i := 0; i < n; i++ {
        for j := i + 1; j < n; j++ {
            x1 := max(bottomLeft[i][0], bottomLeft[j][0])
            y1 := max(bottomLeft[i][1], bottomLeft[j][1])
            x2 := min(topRight[i][0], topRight[j][0])
            y2 := min(topRight[i][1], topRight[j][1])
            w, h := x2-x1, y2-y1
            if w > 0 && h > 0 {
                s := min(w, h)
                if s*s > ans {
                    ans = s * s
                }
            }
        }
    }
    return ans
}
func min(a, b int) int { if a < b { return a }; return b }
func max(a, b int) int { if a > b { return a }; return b }

Java

class Solution {
    public int largestSquareArea(int[][] bottomLeft, int[][] topRight) {
        int n = bottomLeft.length, ans = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int x1 = Math.max(bottomLeft[i][0], bottomLeft[j][0]);
                int y1 = Math.max(bottomLeft[i][1], bottomLeft[j][1]);
                int x2 = Math.min(topRight[i][0], topRight[j][0]);
                int y2 = Math.min(topRight[i][1], topRight[j][1]);
                int w = x2 - x1, h = y2 - y1;
                if (w > 0 && h > 0) ans = Math.max(ans, Math.min(w, h) * Math.min(w, h));
            }
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun largestSquareArea(bottomLeft: Array<IntArray>, topRight: Array<IntArray>): Int {
        val n = bottomLeft.size
        var ans = 0
        for (i in 0 until n) {
            for (j in i + 1 until n) {
                val x1 = maxOf(bottomLeft[i][0], bottomLeft[j][0])
                val y1 = maxOf(bottomLeft[i][1], bottomLeft[j][1])
                val x2 = minOf(topRight[i][0], topRight[j][0])
                val y2 = minOf(topRight[i][1], topRight[j][1])
                val w = x2 - x1
                val h = y2 - y1
                if (w > 0 && h > 0) ans = maxOf(ans, minOf(w, h) * minOf(w, h))
            }
        }
        return ans
    }
}

Python

def largest_square_area(bottomLeft: list[list[int]], topRight: list[list[int]]) -> int:
    n = len(bottomLeft)
    ans = 0
    for i in range(n):
        for j in range(i+1, n):
            x1 = max(bottomLeft[i][0], bottomLeft[j][0])
            y1 = max(bottomLeft[i][1], bottomLeft[j][1])
            x2 = min(topRight[i][0], topRight[j][0])
            y2 = min(topRight[i][1], topRight[j][1])
            w, h = x2 - x1, y2 - y1
            if w > 0 and h > 0:
                ans = max(ans, min(w, h) * min(w, h))
    return ans

Rust

impl Solution {
    pub fn largest_square_area(bottom_left: Vec<Vec<i32>>, top_right: Vec<Vec<i32>>) -> i32 {
        let n = bottom_left.len();
        let mut ans = 0;
        for i in 0..n {
            for j in i+1..n {
                let x1 = bottom_left[i][0].max(bottom_left[j][0]);
                let y1 = bottom_left[i][1].max(bottom_left[j][1]);
                let x2 = top_right[i][0].min(top_right[j][0]);
                let y2 = top_right[i][1].min(top_right[j][1]);
                let w = x2 - x1;
                let h = y2 - y1;
                if w > 0 && h > 0 {
                    let s = w.min(h);
                    ans = ans.max(s * s);
                }
            }
        }
        ans
    }
}

TypeScript

class Solution {
    largestSquareArea(bottomLeft: number[][], topRight: number[][]): number {
        const n = bottomLeft.length;
        let ans = 0;
        for (let i = 0; i < n; i++) {
            for (let j = i + 1; j < n; j++) {
                const x1 = Math.max(bottomLeft[i][0], bottomLeft[j][0]);
                const y1 = Math.max(bottomLeft[i][1], bottomLeft[j][1]);
                const x2 = Math.min(topRight[i][0], topRight[j][0]);
                const y2 = Math.min(topRight[i][1], topRight[j][1]);
                const w = x2 - x1, h = y2 - y1;
                if (w > 0 && h > 0) ans = Math.max(ans, Math.min(w, h) * Math.min(w, h));
            }
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n^2), as we check all pairs of rectangles.
• 🧺 Space complexity: O(1), only a few variables are used for computation.