Problem

There is a game dungeon comprised of n x n rooms arranged in a grid.

You are given a 2D array fruits of size n x n, where fruits[i][j] represents the number of fruits in the room (i, j). Three children will play in the game dungeon, with initial positions at the corner rooms (0, 0), (0, n - 1), and (n - 1, 0).

The children will make exactly n - 1 moves according to the following rules to reach the room (n - 1, n - 1):

  • The child starting from (0, 0) must move from their current room (i, j) to one of the rooms (i + 1, j + 1), (i + 1, j), and (i, j + 1) if the target room exists.
  • The child starting from (0, n - 1) must move from their current room (i, j) to one of the rooms (i + 1, j - 1), (i + 1, j), and (i + 1, j + 1) if the target room exists.
  • The child starting from (n - 1, 0) must move from their current room (i, j) to one of the rooms (i - 1, j + 1), (i, j + 1), and (i + 1, j + 1) if the target room exists.

When a child enters a room, they will collect all the fruits there. If two or more children enter the same room, only one child will collect the fruits, and the room will be emptied after they leave.

Return the maximum number of fruits the children can collect from the dungeon.

Examples

Example 1

1
2
3
4
5
6
7
8
9

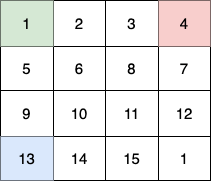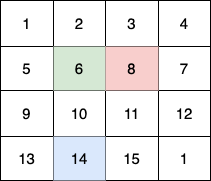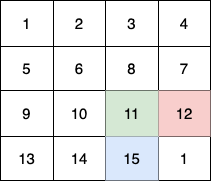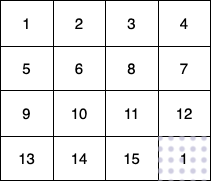
Input: fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]]
Output: 100
Explanation:
In this example:
  * The 1st child (green) moves on the path `(0,0) -> (1,1) -> (2,2) -> (3, 3)`.
  * The 2nd child (red) moves on the path `(0,3) -> (1,2) -> (2,3) -> (3, 3)`.
  * The 3rd child (blue) moves on the path `(3,0) -> (3,1) -> (3,2) -> (3, 3)`.

In total they collect `1 + 6 + 11 + 16 + 4 + 8 + 12 + 13 + 14 + 15 = 100` fruits.

Example 2

1
2
3
4
5
6
7
8

Input: fruits = [[1,1],[1,1]]
Output: 4
Explanation:
In this example:
  * The 1st child moves on the path `(0,0) -> (1,1)`.
  * The 2nd child moves on the path `(0,1) -> (1,1)`.
  * The 3rd child moves on the path `(1,0) -> (1,1)`.
In total they collect `1 + 1 + 1 + 1 = 4` fruits.

Constraints

  • 2 <= n == fruits.length == fruits[i].length <= 1000
  • 0 <= fruits[i][j] <= 1000

Solution

Method 1 – 3D Dynamic Programming (State Compression)

Intuition

The key insight is to recognize that we can decompose this problem into three independent subproblems:

  1. Main diagonal path: The child starting from (0,0) will always take the main diagonal to (n-1, n-1), collecting fruits[i][i] for all i.

  2. Top-right to bottom-right path: The child starting from (0, n-1) needs to reach (n-1, n-1) while staying in the upper-right triangle and avoiding the main diagonal.

  3. Bottom-left to bottom-right path: The child starting from (n-1, 0) needs to reach (n-1, n-1) while staying in the lower-left triangle and avoiding the main diagonal.

Since these three paths don’t overlap (except at the final destination), we can solve each subproblem independently and sum the results.

Approach

  1. Collect main diagonal fruits: These are guaranteed to be collected and don’t interfere with other paths.

  2. Dynamic Programming for two remaining paths:

    • Use 1D DP arrays to track the maximum fruits for each possible position
    • For each step, consider three possible moves: left-diagonal, straight, right-diagonal
    • Use a sliding window approach to optimize memory usage

  3. Combine results: Sum the diagonal fruits with the optimal paths from the other two children.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

class Solution {
public:
    int maxCollectedFruits(vector<vector<int>>& fruits) {
        int n = fruits.size();
        int total = 0;

        // Collect main diagonal fruits (top-left to bottom-right)
        for (int i = 0; i < n; i++) {
            total += fruits[i][i];
        }

        // DP for top-right child path
        vector<int> rightPath(3);
        rightPath[0] = fruits[0][n - 1];

        // DP for bottom-left child path  
        vector<int> bottomPath(3);
        bottomPath[0] = fruits[n - 1][0];

        int window = 2;

        // Process each step from 1 to n-2
        for (int step = 1; step < n - 1; step++) {
            vector<int> newRight(window + 2, 0);
            vector<int> newBottom(window + 2, 0);

            // Update DP arrays for both paths
            for (int dist = 0; dist < window; dist++) {
                // Right path: child moving from top-right
                int left = (dist - 1 >= 0) ? rightPath[dist - 1] : 0;
                int mid = rightPath[dist];
                int right = (dist + 1 < rightPath.size()) ? rightPath[dist + 1] : 0;
                newRight[dist] = max({left, mid, right}) + fruits[step][n - 1 - dist];

                // Bottom path: child moving from bottom-left
                left = (dist - 1 >= 0) ? bottomPath[dist - 1] : 0;
                mid = bottomPath[dist];
                right = (dist + 1 < bottomPath.size()) ? bottomPath[dist + 1] : 0;
                newBottom[dist] = max({left, mid, right}) + fruits[n - 1 - dist][step];
            }

            rightPath = newRight;
            bottomPath = newBottom;

            // Adjust window size based on grid constraints
            if (window - n + 4 + step <= 1) {
                window += 1;
            } else if (window - n + 3 + step > 1) {
                window -= 1;
            }
        }

        return total + rightPath[0] + bottomPath[0];
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

func maxCollectedFruits(fruits [][]int) int {
    n := len(fruits)
    total := 0

    // Collect main diagonal fruits (top-left to bottom-right)
    for i := 0; i < n; i++ {
        total += fruits[i][i]
    }

    // DP for top-right child path
    rightPath := make([]int, 3)
    rightPath[0] = fruits[0][n-1]

    // DP for bottom-left child path  
    bottomPath := make([]int, 3)
    bottomPath[0] = fruits[n-1][0]

    window := 2

    // Process each step from 1 to n-2
    for step := 1; step < n-1; step++ {
        newRight := make([]int, window+2)
        newBottom := make([]int, window+2)

        // Update DP arrays for both paths
        for dist := 0; dist < window; dist++ {
            // Right path: child moving from top-right
            left := 0
            if dist-1 >= 0 {
                left = rightPath[dist-1]
            }
            mid := rightPath[dist]
            right := 0
            if dist+1 < len(rightPath) {
                right = rightPath[dist+1]
            }
            newRight[dist] = max(left, max(mid, right)) + fruits[step][n-1-dist]

            // Bottom path: child moving from bottom-left
            left = 0
            if dist-1 >= 0 {
                left = bottomPath[dist-1]
            }
            mid = bottomPath[dist]
            right = 0
            if dist+1 < len(bottomPath) {
                right = bottomPath[dist+1]
            }
            newBottom[dist] = max(left, max(mid, right)) + fruits[n-1-dist][step]
        }

        rightPath = newRight
        bottomPath = newBottom

        // Adjust window size based on grid constraints
        if window-n+4+step <= 1 {
            window++
        } else if window-n+3+step > 1 {
            window--
        }
    }

    return total + rightPath[0] + bottomPath[0]
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

class Solution {
    public int maxCollectedFruits(int[][] fruits) {
        int n = fruits.length;
        int total = 0;

        // Collect main diagonal fruits (top-left to bottom-right)
        for (int i = 0; i < n; i++) {
            total += fruits[i][i];
        }

        // DP for top-right child path
        int[] rightPath = new int[3];
        rightPath[0] = fruits[0][n - 1];

        // DP for bottom-left child path  
        int[] bottomPath = new int[3];
        bottomPath[0] = fruits[n - 1][0];

        int window = 2;

        // Process each step from 1 to n-2
        for (int step = 1; step < n - 1; step++) {
            int[] newRight = new int[window + 2];
            int[] newBottom = new int[window + 2];

            // Update DP arrays for both paths
            for (int dist = 0; dist < window; dist++) {
                // Right path: child moving from top-right
                int left = (dist - 1 >= 0) ? rightPath[dist - 1] : 0;
                int mid = rightPath[dist];
                int right = (dist + 1 < rightPath.length) ? rightPath[dist + 1] : 0;
                newRight[dist] = Math.max(left, Math.max(mid, right)) + fruits[step][n - 1 - dist];

                // Bottom path: child moving from bottom-left
                left = (dist - 1 >= 0) ? bottomPath[dist - 1] : 0;
                mid = bottomPath[dist];
                right = (dist + 1 < bottomPath.length) ? bottomPath[dist + 1] : 0;
                newBottom[dist] = Math.max(left, Math.max(mid, right)) + fruits[n - 1 - dist][step];
            }

            rightPath = newRight;
            bottomPath = newBottom;

            // Adjust window size based on grid constraints
            if (window - n + 4 + step <= 1) {
                window += 1;
            } else if (window - n + 3 + step > 1) {
                window -= 1;
            }
        }

        return total + rightPath[0] + bottomPath[0];
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

class Solution {
    fun maxCollectedFruits(fruits: Array<IntArray>): Int {
        val n = fruits.size
        var total = 0

        // Collect main diagonal fruits (top-left to bottom-right)
        for (i in 0 until n) {
            total += fruits[i][i]
        }

        // DP for top-right child path
        var rightPath = IntArray(3)
        rightPath[0] = fruits[0][n - 1]

        // DP for bottom-left child path  
        var bottomPath = IntArray(3)
        bottomPath[0] = fruits[n - 1][0]

        var window = 2

        // Process each step from 1 to n-2
        for (step in 1 until n - 1) {
            val newRight = IntArray(window + 2)
            val newBottom = IntArray(window + 2)

            // Update DP arrays for both paths
            for (dist in 0 until window) {
                // Right path: child moving from top-right
                val left = if (dist - 1 >= 0) rightPath[dist - 1] else 0
                val mid = rightPath[dist]
                val right = if (dist + 1 < rightPath.size) rightPath[dist + 1] else 0
                newRight[dist] = maxOf(left, mid, right) + fruits[step][n - 1 - dist]

                // Bottom path: child moving from bottom-left
                val leftBottom = if (dist - 1 >= 0) bottomPath[dist - 1] else 0
                val midBottom = bottomPath[dist]
                val rightBottom = if (dist + 1 < bottomPath.size) bottomPath[dist + 1] else 0
                newBottom[dist] = maxOf(leftBottom, midBottom, rightBottom) + fruits[n - 1 - dist][step]
            }

            rightPath = newRight
            bottomPath = newBottom

            // Adjust window size based on grid constraints
            if (window - n + 4 + step <= 1) {
                window += 1
            } else if (window - n + 3 + step > 1) {
                window -= 1
            }
        }

        return total + rightPath[0] + bottomPath[0]
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

class Solution:
    def maxCollectedFruits(self, fruits: list[list[int]]) -> int:
        n = len(fruits)
        total = 0

        # Collect main diagonal fruits (top-left to bottom-right)
        for i in range(n):
            total += fruits[i][i]

        # DP for top-right child path
        right_path = [0] * 3
        right_path[0] = fruits[0][n - 1]

        # DP for bottom-left child path  
        bottom_path = [0] * 3
        bottom_path[0] = fruits[n - 1][0]

        window = 2

        # Process each step from 1 to n-2
        for step in range(1, n - 1):
            new_right = [0] * (window + 2)
            new_bottom = [0] * (window + 2)

            # Update DP arrays for both paths
            for dist in range(window):
                # Right path: child moving from top-right
                left = right_path[dist - 1] if dist - 1 >= 0 else 0
                mid = right_path[dist]
                right = right_path[dist + 1] if dist + 1 < len(right_path) else 0
                new_right[dist] = max(left, mid, right) + fruits[step][n - 1 - dist]

                # Bottom path: child moving from bottom-left
                left = bottom_path[dist - 1] if dist - 1 >= 0 else 0
                mid = bottom_path[dist]
                right = bottom_path[dist + 1] if dist + 1 < len(bottom_path) else 0
                new_bottom[dist] = max(left, mid, right) + fruits[n - 1 - dist][step]

            right_path = new_right
            bottom_path = new_bottom

            # Adjust window size based on grid constraints
            if window - n + 4 + step <= 1:
                window += 1
            elif window - n + 3 + step > 1:
                window -= 1

        return total + right_path[0] + bottom_path[0]
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

impl Solution {
    pub fn max_collected_fruits(fruits: Vec<Vec<i32>>) -> i32 {
        let n = fruits.len();
        let mut total = 0;

        // Collect main diagonal fruits (top-left to bottom-right)
        for i in 0..n {
            total += fruits[i][i];
        }

        // DP for top-right child path
        let mut right_path = vec![0; 3];
        right_path[0] = fruits[0][n - 1];

        // DP for bottom-left child path
        let mut bottom_path = vec![0; 3];
        bottom_path[0] = fruits[n - 1][0];

        let mut window = 2;

        // Process each step from 1 to n-2
        for step in 1..n - 1 {
            let mut new_right = vec![0; window + 2];
            let mut new_bottom = vec![0; window + 2];

            // Update DP arrays for both paths
            for dist in 0..window {
                // Right path: child moving from top-right
                let left = if dist > 0 { right_path[dist - 1] } else { 0 };
                let mid = right_path[dist];
                let right = if dist + 1 < right_path.len() { right_path[dist + 1] } else { 0 };
                new_right[dist] = [left, mid, right].iter().max().unwrap() + fruits[step][n - 1 - dist];

                // Bottom path: child moving from bottom-left
                let left = if dist > 0 { bottom_path[dist - 1] } else { 0 };
                let mid = bottom_path[dist];
                let right = if dist + 1 < bottom_path.len() { bottom_path[dist + 1] } else { 0 };
                new_bottom[dist] = [left, mid, right].iter().max().unwrap() + fruits[n - 1 - dist][step];
            }

            right_path = new_right;
            bottom_path = new_bottom;

            // Adjust window size based on grid constraints
            if window as i32 - n as i32 + 4 + step as i32 <= 1 {
                window += 1;
            } else if window as i32 - n as i32 + 3 + step as i32 > 1 {
                window -= 1;
            }
        }

        total + right_path[0] + bottom_path[0]
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

function maxCollectedFruits(fruits: number[][]): number {
    const n = fruits.length;
    let total = 0;

    // Collect main diagonal fruits (top-left to bottom-right)
    for (let i = 0; i < n; i++) {
        total += fruits[i][i];
    }

    // DP for top-right child path
    let rightPath = new Array(3).fill(0);
    rightPath[0] = fruits[0][n - 1];

    // DP for bottom-left child path
    let bottomPath = new Array(3).fill(0);
    bottomPath[0] = fruits[n - 1][0];

    let window = 2;

    // Process each step from 1 to n-2
    for (let step = 1; step < n - 1; step++) {
        const newRight = new Array(window + 2).fill(0);
        const newBottom = new Array(window + 2).fill(0);

        // Update DP arrays for both paths
        for (let dist = 0; dist < window; dist++) {
            // Right path: child moving from top-right
            const left = dist - 1 >= 0 ? rightPath[dist - 1] : 0;
            const mid = rightPath[dist];
            const right = dist + 1 < rightPath.length ? rightPath[dist + 1] : 0;
            newRight[dist] = Math.max(left, mid, right) + fruits[step][n - 1 - dist];

            // Bottom path: child moving from bottom-left
            const leftBot = dist - 1 >= 0 ? bottomPath[dist - 1] : 0;
            const midBot = bottomPath[dist];
            const rightBot = dist + 1 < bottomPath.length ? bottomPath[dist + 1] : 0;
            newBottom[dist] = Math.max(leftBot, midBot, rightBot) + fruits[n - 1 - dist][step];
        }

        rightPath = newRight;
        bottomPath = newBottom;

        // Adjust window size based on grid constraints
        if (window - n + 4 + step <= 1) {
            window++;
        } else if (window - n + 3 + step > 1) {
            window--;
        }
    }

    return total + rightPath[0] + bottomPath[0];
}

Complexity

  • ⏰ Time complexity: O(n^2), using optimized sliding window approach with decomposed paths.
  • 🧺 Space complexity: O(n), for the DP arrays tracking path states.- array