Problem

You are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1’s in grid lie inside these rectangles.

Example 1

1
2
3
4
5
6

Input: grid = [[1,0,1],[1,1,1]]
Output: 5
Explanation:
  * The 1's at `(0, 0)` and `(1, 0)` are covered by a rectangle of area 2.
  * The 1's at `(0, 2)` and `(1, 2)` are covered by a rectangle of area 2.
  * The 1 at `(1, 1)` is covered by a rectangle of area 1.

Example 2

1
2
3
4
5
6

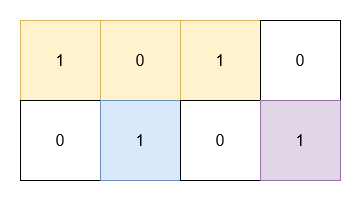
Input: grid = [[1,0,1,0],[0,1,0,1]]
Output: 5
Explanation:
  * The 1's at `(0, 0)` and `(0, 2)` are covered by a rectangle of area 3.
  * The 1 at `(1, 1)` is covered by a rectangle of area 1.
  * The 1 at `(1, 3)` is covered by a rectangle of area 1.

Constraints

  • 1 <= grid.length, grid[i].length <= 30
  • grid[i][j] is either 0 or 1.
  • The input is generated such that there are at least three 1’s in grid.
Similar Problems

Solution

Method 1 – Brute Force All Rectangle Partitions (for Small Grids)

Intuition

We need to cover all 1’s in the grid with 3 non-overlapping rectangles of non-zero area, minimizing the total area. For small grids, we can brute-force all possible ways to partition the grid into 3 rectangles, check if all 1’s are covered, and compute the minimum area sum.

Approach

  1. For each possible way to split the grid into 3 rectangles (by vertical and/or horizontal cuts), enumerate all possible rectangles.
  2. For each combination of 3 rectangles, check:
    • All rectangles have non-zero area.
    • Rectangles do not overlap.
    • All 1’s in the grid are covered by at least one rectangle.
  3. Compute the sum of the areas for valid combinations and track the minimum.
  4. Return the minimum area sum found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

class Solution {
public:
  int minimumSum(vector<vector<int>>& grid) {
    int m = grid.size(), n = grid[0].size();
    vector<pair<int,int>> ones;
    for (int i = 0; i < m; ++i)
      for (int j = 0; j < n; ++j)
        if (grid[i][j]) ones.emplace_back(i, j);
    if (ones.empty()) return 0;
    int ans = numeric_limits<int>::max();

    for (int r1 = 0; r1 < m; ++r1)
      for (int r2 = r1; r2 < m; ++r2)
        for (int c1 = 0; c1 < n; ++c1)
          for (int c2 = c1; c2 < n; ++c2) {
            unordered_set<int> rect1;
            for (int i = r1; i <= r2; ++i)
              for (int j = c1; j <= c2; ++j)
                rect1.insert(i * n + j);
            bool covers1 = false;
            for (auto &p : ones) if (rect1.count(p.first * n + p.second)) { covers1 = true; break; }
            if (!covers1) continue;

            for (int rr1 = 0; rr1 < m; ++rr1)
              for (int rr2 = rr1; rr2 < m; ++rr2)
                for (int cc1 = 0; cc1 < n; ++cc1)
                  for (int cc2 = cc1; cc2 < n; ++cc2) {
                    unordered_set<int> rect2;
                    bool overlap = false;
                    for (int i = rr1; i <= rr2 && !overlap; ++i)
                      for (int j = cc1; j <= cc2; ++j) {
                        int code = i * n + j;
                        if (rect1.count(code)) { overlap = true; break; }
                        rect2.insert(code);
                      }
                    if (overlap) continue;
                    bool covers2 = false;
                    for (auto &p : ones) if (rect2.count(p.first * n + p.second)) { covers2 = true; break; }
                    if (!covers2) continue;

                    unordered_set<int> covered = rect1;
                    covered.insert(rect2.begin(), rect2.end());
                    vector<pair<int,int>> left;
                    for (auto &p : ones) if (!covered.count(p.first * n + p.second)) left.push_back(p);
                    if (left.empty()) continue;

                    int minr = numeric_limits<int>::max(), maxr = numeric_limits<int>::min();
                    int minc = numeric_limits<int>::max(), maxc = numeric_limits<int>::min();
                    for (auto &p : left) {
                      minr = min(minr, p.first);
                      maxr = max(maxr, p.first);
                      minc = min(minc, p.second);
                      maxc = max(maxc, p.second);
                    }
                    int area3 = (maxr - minr + 1) * (maxc - minc + 1);
                    int area1 = (r2 - r1 + 1) * (c2 - c1 + 1);
                    int area2 = (rr2 - rr1 + 1) * (cc2 - cc1 + 1);
                    ans = min(ans, area1 + area2 + area3);
                  }
          }
    return ans == numeric_limits<int>::max() ? 0 : ans;
  }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

class Solution {
  public int minimumSum(int[][] grid) {
    int m = grid.length, n = grid[0].length;
    List<int[]> ones = new ArrayList<>();
    for (int i = 0; i < m; ++i)
      for (int j = 0; j < n; ++j)
        if (grid[i][j] == 1) ones.add(new int[]{i, j});
    if (ones.isEmpty()) return 0;
    int ans = Integer.MAX_VALUE;

    for (int r1 = 0; r1 < m; ++r1)
      for (int r2 = r1; r2 < m; ++r2)
        for (int c1 = 0; c1 < n; ++c1)
          for (int c2 = c1; c2 < n; ++c2) {
            Set<Integer> rect1 = new HashSet<>();
            for (int i = r1; i <= r2; ++i)
              for (int j = c1; j <= c2; ++j)
                rect1.add(i * n + j);
            boolean covers1 = false;
            for (int[] p : ones) if (rect1.contains(p[0] * n + p[1])) { covers1 = true; break; }
            if (!covers1) continue;

            for (int rr1 = 0; rr1 < m; ++rr1)
              for (int rr2 = rr1; rr2 < m; ++rr2)
                for (int cc1 = 0; cc1 < n; ++cc1)
                  for (int cc2 = cc1; cc2 < n; ++cc2) {
                    Set<Integer> rect2 = new HashSet<>();
                    boolean overlap = false;
                    outer:
                    for (int i = rr1; i <= rr2; ++i) {
                      for (int j = cc1; j <= cc2; ++j) {
                        int code = i * n + j;
                        if (rect1.contains(code)) { overlap = true; break outer; }
                        rect2.add(code);
                      }
                    }
                    if (overlap) continue;
                    boolean covers2 = false;
                    for (int[] p : ones) if (rect2.contains(p[0] * n + p[1])) { covers2 = true; break; }
                    if (!covers2) continue;

                    Set<Integer> covered = new HashSet<>(rect1);
                    covered.addAll(rect2);
                    List<int[]> left = new ArrayList<>();
                    for (int[] p : ones) if (!covered.contains(p[0] * n + p[1])) left.add(p);
                    if (left.isEmpty()) continue;

                    int minr = Integer.MAX_VALUE, maxr = Integer.MIN_VALUE;
                    int minc = Integer.MAX_VALUE, maxc = Integer.MIN_VALUE;
                    for (int[] p : left) {
                      minr = Math.min(minr, p[0]);
                      maxr = Math.max(maxr, p[0]);
                      minc = Math.min(minc, p[1]);
                      maxc = Math.max(maxc, p[1]);
                    }
                    int area3 = (maxr - minr + 1) * (maxc - minc + 1);
                    int area1 = (r2 - r1 + 1) * (c2 - c1 + 1);
                    int area2 = (rr2 - rr1 + 1) * (cc2 - cc1 + 1);
                    ans = Math.min(ans, area1 + area2 + area3);
                  }
          }
    return ans == Integer.MAX_VALUE ? 0 : ans;
  }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

class Solution:
  def minimumSum(self, grid: List[List[int]]) -> int:
    m, n = len(grid), len(grid[0])
    ones = [(i,j) for i in range(m) for j in range(n) if grid[i][j]==1]
    if not ones:
      return 0
    ans = float('inf')
    # Try all possible rectangles for the first
    for r1 in range(m):
      for r2 in range(r1, m):
        for c1 in range(n):
          for c2 in range(c1, n):
            rect1 = set((i,j) for i in range(r1,r2+1) for j in range(c1,c2+1))
            if not any((i,j) in rect1 for (i,j) in ones):
              continue
            # Try all possible rectangles for the second
            for rr1 in range(m):
              for rr2 in range(rr1, m):
                for cc1 in range(n):
                  for cc2 in range(cc1, n):
                    rect2 = set((i,j) for i in range(rr1,rr2+1) for j in range(cc1,cc2+1))
                    if rect1 & rect2:
                      continue
                    if not any((i,j) in rect2 for (i,j) in ones):
                      continue
                    # Third rectangle covers the rest
                    covered = rect1 | rect2
                    left = [p for p in ones if p not in covered]
                    if not left:
                      continue
                    minr = min(i for i,j in left)
                    maxr = max(i for i,j in left)
                    minc = min(j for i,j in left)
                    maxc = max(j for i,j in left)
                    area3 = (maxr-minr+1)*(maxc-minc+1)
                    area1 = (r2-r1+1)*(c2-c1+1)
                    area2 = (rr2-rr1+1)*(cc2-cc1+1)
                    total = area1+area2+area3
                    ans = min(ans, total)
    return ans if ans!=float('inf') else 0

Complexity

  • ⏰ Time complexity: O((m^2 n^2)^2), feasible only for very small grids (e.g., m,n <= 6).
  • 🧺 Space complexity: O(mn), for storing rectangles and positions.

Method 2 — Partition enumeration reusing the bounding-rectangle helper

Intuition

We can reuse the small helper from “Find the Minimum Area to Cover All Ones I” that computes the minimum-area axis-aligned rectangle enclosing all 1’s inside a given submatrix. Instead of enumerating arbitrary rectangles for all three pieces, we enumerate a small set of partition shapes (horizontal/vertical cuts and combinations) that cover all ways to split the grid into three non-overlapping rectangular regions. For each partition we compute the three submatrix bounding rectangles (using the helper) and sum their areas. This avoids enumerating every possible rectangle combination and is far cheaper in practice than the brute-force method.

Here are the six possible cases to iterate on:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

Case 1 — Top block + two bottom blocks (bottom split vertically):

+---------+
|    1    |
+---+-----+
| 2 |  3  |
+---+-----+

Case 2 — Left block + two right blocks (right split horizontally):

+---+-----+
| 1 |  2  |
|   |-----|
|   |  3  |
+---+-----+

Case 3 — Right block + two left blocks (mirror of Case 2):

+-----+---+
| 2   | 1 |
|-----|   |
| 3   |   |
+-----+---+

Case 4 — Bottom block + two top blocks (mirror of Case 1):

+---+-----+
| 2 |  3  |
+---+-----+
|    1    |
+---------+

Case 5 — Three horizontal strips:

+--------+
|   1    |
+--------+
|   2    |
+--------+
|   3    |
+--------+

Case 6 — Three vertical strips:

+---+---+---+
| 1 | 2 | 3 |
+---+---+---+

Approach

  • Implement a helper areaOfOnes(grid, st_i, en_i, st_j, en_j) that returns the area of the smallest rectangle that covers all 1’s inside the inclusive submatrix [st_i..en_i] x [st_j..en_j] (or 0 if none).
  • Enumerate the standard partition templates (top/bottom split with a bottom split into two, left/right split with right split into two, mirrored variants, three horizontal strips, three vertical strips). For each partition, call the helper for the three parts and keep the minimum total area found.
  • This reuses the O(size_of_submatrix) scanning helper instead of constructing arbitrary rectangles, making it much faster than the full brute-force enumeration.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

class Solution {
public:
  int minimumSum(vector<vector<int>>& grid) {
    int m = grid.size(), n = grid[0].size();
    int ans = numeric_limits<int>::max();
    int one, two, three;

    // 1) Top block + two blocks in the bottom row (split by a vertical line)
    for (int i = 0; i < m; ++i) {
      one = areaOfOnes(grid, 0, i, 0, n - 1);
      for (int j = 0; j < n; ++j) {
        two = areaOfOnes(grid, i + 1, m - 1, 0, j);
        three = areaOfOnes(grid, i + 1, m - 1, j + 1, n - 1);
        ans = min(ans, one + two + three);
      }
    }

    // 2) Left block + two blocks on the right (split by a horizontal line)
    for (int j = 0; j < n; ++j) {
      one = areaOfOnes(grid, 0, m - 1, 0, j);
      for (int i = 0; i < m; ++i) {
        two = areaOfOnes(grid, 0, i, j + 1, n - 1);
        three = areaOfOnes(grid, i + 1, m - 1, j + 1, n - 1);
        ans = min(ans, one + two + three);
      }
    }

    // 3) Right block + two blocks on the left (mirror of previous)
    for (int j = n - 1; j >= 0; --j) {
      one = areaOfOnes(grid, 0, m - 1, j + 1, n - 1);
      for (int i = 0; i < m; ++i) {
        two = areaOfOnes(grid, 0, i, 0, j);
        three = areaOfOnes(grid, i + 1, m - 1, 0, j);
        ans = min(ans, one + two + three);
      }
    }

    // 4) Bottom block + two blocks on the top (mirror of 1)
    for (int i = m - 1; i >= 0; --i) {
      one = areaOfOnes(grid, i + 1, m - 1, 0, n - 1);
      for (int j = 0; j < n; ++j) {
        two = areaOfOnes(grid, 0, i, 0, j);
        three = areaOfOnes(grid, 0, i, j + 1, n - 1);
        ans = min(ans, one + two + three);
      }
    }

    // 5) Three horizontal strips
    for (int i = 0; i < m; ++i) {
      for (int j = i + 1; j < m; ++j) {
        one = areaOfOnes(grid, 0, i, 0, n - 1);
        two = areaOfOnes(grid, i + 1, j, 0, n - 1);
        three = areaOfOnes(grid, j + 1, m - 1, 0, n - 1);
        ans = min(ans, one + two + three);
      }
    }

    // 6) Three vertical strips
    for (int i = 0; i < n; ++i) {
      for (int j = i + 1; j < n; ++j) {
        one = areaOfOnes(grid, 0, m - 1, 0, i);
        two = areaOfOnes(grid, 0, m - 1, i + 1, j);
        three = areaOfOnes(grid, 0, m - 1, j + 1, n - 1);
        ans = min(ans, one + two + three);
      }
    }

    return ans == numeric_limits<int>::max() ? 0 : ans;
  }

private:
  int areaOfOnes(vector<vector<int>>& grid, int st_i, int en_i, int st_j, int en_j) {
    if (st_i > en_i || st_j > en_j) return 0;
    int minr = numeric_limits<int>::max(), maxr = numeric_limits<int>::min();
    int minc = numeric_limits<int>::max(), maxc = numeric_limits<int>::min();
    bool found = false;
    for (int i = st_i; i <= en_i; ++i) {
      for (int j = st_j; j <= en_j; ++j) {
        if (grid[i][j]) {
          found = true;
          minr = min(minr, i);
          maxr = max(maxr, i);
          minc = min(minc, j);
          maxc = max(maxc, j);
        }
      }
    }
    return found ? (maxr - minr + 1) * (maxc - minc + 1) : 0;
  }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

class Solution {
  // Method 2: optimized partition-based enumeration that reuses areaOfOnes
  public int minimumSum(int[][] grid) {
    int m = grid.length, n = grid[0].length;
    int ans = Integer.MAX_VALUE;
    int one, two, three;

    // 1) Top block + two blocks in the bottom row (split by a vertical line)
    for (int i = 0; i < m; ++i) {
      one = areaOfOnes(grid, 0, i, 0, n - 1);
      for (int j = 0; j < n; ++j) {
        two = areaOfOnes(grid, i + 1, m - 1, 0, j);
        three = areaOfOnes(grid, i + 1, m - 1, j + 1, n - 1);
        ans = Math.min(ans, one + two + three);
      }
    }

    // 2) Left block + two blocks on the right (split by a horizontal line)
    for (int j = 0; j < n; ++j) {
      one = areaOfOnes(grid, 0, m - 1, 0, j);
      for (int i = 0; i < m; ++i) {
        two = areaOfOnes(grid, 0, i, j + 1, n - 1);
        three = areaOfOnes(grid, i + 1, m - 1, j + 1, n - 1);
        ans = Math.min(ans, one + two + three);
      }
    }

    // 3) Right block + two blocks on the left (mirror of previous)
    for (int j = n - 1; j >= 0; --j) {
      one = areaOfOnes(grid, 0, m - 1, j + 1, n - 1);
      for (int i = 0; i < m; ++i) {
        two = areaOfOnes(grid, 0, i, 0, j);
        three = areaOfOnes(grid, i + 1, m - 1, 0, j);
        ans = Math.min(ans, one + two + three);
      }
    }

    // 4) Bottom block + two blocks on the top (mirror of 1)
    for (int i = m - 1; i >= 0; --i) {
      one = areaOfOnes(grid, i + 1, m - 1, 0, n - 1);
      for (int j = 0; j < n; ++j) {
        two = areaOfOnes(grid, 0, i, 0, j);
        three = areaOfOnes(grid, 0, i, j + 1, n - 1);
        ans = Math.min(ans, one + two + three);
      }
    }

    // 5) Three horizontal strips
    for (int i = 0; i < m; ++i) {
      for (int j = i + 1; j < m; ++j) {
        one = areaOfOnes(grid, 0, i, 0, n - 1);
        two = areaOfOnes(grid, i + 1, j, 0, n - 1);
        three = areaOfOnes(grid, j + 1, m - 1, 0, n - 1);
        ans = Math.min(ans, one + two + three);
      }
    }

    // 6) Three vertical strips
    for (int i = 0; i < n; ++i) {
      for (int j = i + 1; j < n; ++j) {
        one = areaOfOnes(grid, 0, m - 1, 0, i);
        two = areaOfOnes(grid, 0, m - 1, i + 1, j);
        three = areaOfOnes(grid, 0, m - 1, j + 1, n - 1);
        ans = Math.min(ans, one + two + three);
      }
    }

    return ans == Integer.MAX_VALUE ? 0 : ans;
  }

  // Helper: area of bounding rectangle covering all ones in inclusive submatrix.
  private int areaOfOnes(int[][] grid, int st_i, int en_i, int st_j, int en_j) {
    if (st_i > en_i || st_j > en_j) return 0;
    int minr = Integer.MAX_VALUE, maxr = -1, minc = Integer.MAX_VALUE, maxc = -1;
    boolean found = false;
    for (int i = st_i; i <= en_i; ++i) {
      for (int j = st_j; j <= en_j; ++j) {
        if (grid[i][j] == 1) {
          found = true;
          minr = Math.min(minr, i);
          maxr = Math.max(maxr, i);
          minc = Math.min(minc, j);
          maxc = Math.max(maxc, j);
        }
      }
    }
    return found ? (maxr - minr + 1) * (maxc - minc + 1) : 0;
  }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

from typing import List

class Solution:
  # Method 2: optimized partition-based enumeration using area_of_ones helper
  def minimumSum(self, grid: List[List[int]]) -> int:
    m, n = len(grid), len(grid[0])
    INF = 10**9
    ans = INF

    # 1) Top block + two blocks in the bottom row (split by a vertical line)
    for i in range(m):
      one = self.area_of_ones(grid, 0, i, 0, n - 1)
      for j in range(n):
        two = self.area_of_ones(grid, i + 1, m - 1, 0, j)
        three = self.area_of_ones(grid, i + 1, m - 1, j + 1, n - 1)
        ans = min(ans, one + two + three)

    # 2) Left block + two blocks on the right (split by a horizontal line)
    for j in range(n):
      one = self.area_of_ones(grid, 0, m - 1, 0, j)
      for i in range(m):
        two = self.area_of_ones(grid, 0, i, j + 1, n - 1)
        three = self.area_of_ones(grid, i + 1, m - 1, j + 1, n - 1)
        ans = min(ans, one + two + three)

    # 3) Right block + two blocks on the left (mirror of previous)
    for j in range(n - 1, -1, -1):
      one = self.area_of_ones(grid, 0, m - 1, j + 1, n - 1)
      for i in range(m):
        two = self.area_of_ones(grid, 0, i, 0, j)
        three = self.area_of_ones(grid, i + 1, m - 1, 0, j)
        ans = min(ans, one + two + three)

    # 4) Bottom block + two blocks on the top (mirror of 1)
    for i in range(m - 1, -1, -1):
      one = self.area_of_ones(grid, i + 1, m - 1, 0, n - 1)
      for j in range(n):
        two = self.area_of_ones(grid, 0, i, 0, j)
        three = self.area_of_ones(grid, 0, i, j + 1, n - 1)
        ans = min(ans, one + two + three)

    # 5) Three horizontal strips
    for i in range(m):
      for j in range(i + 1, m):
        one = self.area_of_ones(grid, 0, i, 0, n - 1)
        two = self.area_of_ones(grid, i + 1, j, 0, n - 1)
        three = self.area_of_ones(grid, j + 1, m - 1, 0, n - 1)
        ans = min(ans, one + two + three)

    # 6) Three vertical strips
    for i in range(n):
      for j in range(i + 1, n):
        one = self.area_of_ones(grid, 0, m - 1, 0, i)
        two = self.area_of_ones(grid, 0, m - 1, i + 1, j)
        three = self.area_of_ones(grid, 0, m - 1, j + 1, n - 1)
        ans = min(ans, one + two + three)

    return 0 if ans == INF else ans

  def area_of_ones(self, grid: List[List[int]], st_i: int, en_i: int, st_j: int, en_j: int) -> int:
    # inclusive bounds; return 0 if invalid range or no ones
    if st_i > en_i or st_j > en_j:
      return 0
    minr, maxr = 10**9, -1
    minc, maxc = 10**9, -1
    found = False
    for i in range(st_i, en_i + 1):
      for j in range(st_j, en_j + 1):
        if grid[i][j] == 1:
          found = True
          minr = min(minr, i)
          maxr = max(maxr, i)
          minc = min(minc, j)
          maxc = max(maxc, j)
    return (maxr - minr + 1) * (maxc - minc + 1) if found else 0

Complexity

  • ⏰ Time complexity: O(m^2 * n^2), in the worst case (each partition template runs over O(m*n) splits and the helper scans submatrices). This is substantially faster than the full brute-force enumeration of arbitrary rectangle triples (which is effectively O((m^2 n^2)^2)).
  • 🧺 Space complexity: O(1) for extra memory.