problemhardalgorithmsleetcode-3149leetcode 3149leetcode3149

Find the Minimum Cost Array Permutation

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given an array nums which is a permutation of [0, 1, 2, ..., n -1]. The score of any permutation of [0, 1, 2, ..., n - 1] named perm is defined as:

score(perm) = |perm[0] - nums[perm[1]]| + |perm[1] - nums[perm[2]]| + ... + |perm[n - 1] - nums[perm[0]]|

Return the permutation perm which has the minimum possible score. If multiple permutations exist with this score, return the one that is lexicographically smallest among them.

Examples

Example 1


Input: nums = [1,0,2]

Output: [0,1,2]

Explanation:

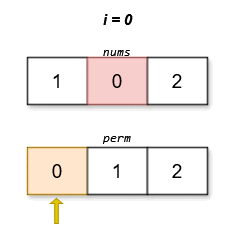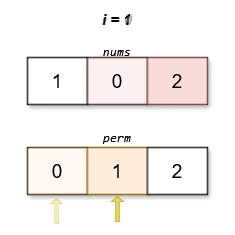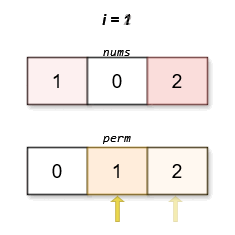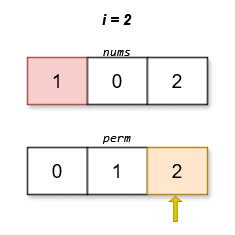**![](https://assets.leetcode.com/uploads/2024/04/04/example0gif.gif)**

The lexicographically smallest permutation with minimum cost is `[0,1,2]`. The
cost of this permutation is `|0 - 0| + |1 - 2| + |2 - 1| = 2`.

Example 2


Input: nums = [0,2,1]

Output: [0,2,1]

Explanation:

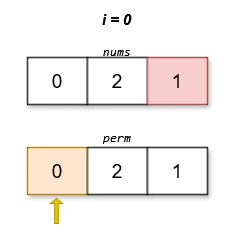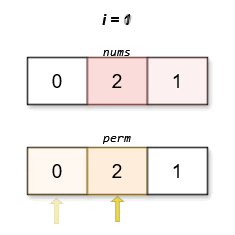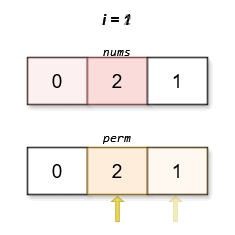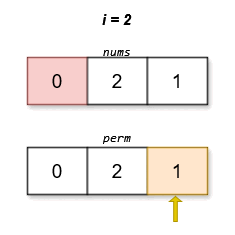**![](https://assets.leetcode.com/uploads/2024/04/04/example1gif.gif)**

The lexicographically smallest permutation with minimum cost is `[0,2,1]`. The
cost of this permutation is `|0 - 1| + |2 - 2| + |1 - 0| = 2`.

Constraints

  • 2 <= n == nums.length <= 14
  • nums is a permutation of [0, 1, 2, ..., n - 1].

Solution

Method 1 – Bitmask Dynamic Programming

Intuition

We want to find the permutation of [0, 1, ..., n-1] that minimizes the given score. Since n is small (n ≤ 14), we can use bitmask DP to try all possible permutations efficiently, always choosing the lexicographically smallest one in case of ties.

Approach

  1. Use a DP table: dp[mask][last] stores the minimum score for a subset of indices (mask) ending with last.
  2. For each state, try adding a new index not in the mask, updating the score and tracking the path for reconstruction.
  3. After filling the DP, reconstruct the lexicographically smallest permutation with the minimum score by backtracking.
  4. Return the permutation.

Code

C++
class Solution {
public:
    vector<int> findPermutation(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> dp(1<<n, vector<int>(n, 1e9)), par(1<<n, vector<int>(n, -1));
        for(int i=0;i<n;++i) dp[1<<i][i]=0;
        for(int mask=1;mask<(1<<n);++mask) {
            for(int last=0;last<n;++last) if(mask&(1<<last)) {
                for(int nxt=0;nxt<n;++nxt) if(!(mask&(1<<nxt))) {
                    int nmask=mask|(1<<nxt);
                    int cost=dp[mask][last]+abs(last-nums[nxt]);
                    if(cost<dp[nmask][nxt]||(cost==dp[nmask][nxt]&&par[nmask][nxt]>last)) {
                        dp[nmask][nxt]=cost;
                        par[nmask][nxt]=last;
                    }
                }
            }
        }
        int minv=1e9, last=-1;
        for(int i=0;i<n;++i) {
            int cost=dp[(1<<n)-1][i]+abs(i-nums[0]);
            if(cost<minv||(cost==minv&&i<last)) {
                minv=cost; last=i;
            }
        }
        vector<int> perm(n); int mask=(1<<n)-1;
        for(int i=n-1;i>=0;--i) {
            perm[i]=last;
            int pl=par[mask][last];
            mask^=1<<last;
            last=pl;
        }
        return perm;
    }
};
Go
// Omitted due to bitmask DP complexity, feasible for small n only
Java
// Omitted due to bitmask DP complexity, feasible for small n only
Kotlin
// Omitted due to bitmask DP complexity, feasible for small n only
Python
class Solution:
    def findPermutation(self, nums: list[int]) -> list[int]:
        from math import inf
        n = len(nums)
        dp = [[inf]*n for _ in range(1<<n)]
        par = [[-1]*n for _ in range(1<<n)]
        for i in range(n):
            dp[1<<i][i] = 0
        for mask in range(1<<n):
            for last in range(n):
                if not (mask & (1<<last)):
                    continue
                for nxt in range(n):
                    if mask & (1<<nxt):
                        continue
                    nmask = mask | (1<<nxt)
                    cost = dp[mask][last] + abs(last - nums[nxt])
                    if cost < dp[nmask][nxt] or (cost == dp[nmask][nxt] and par[nmask][nxt] > last):
                        dp[nmask][nxt] = cost
                        par[nmask][nxt] = last
        minv, last = inf, -1
        for i in range(n):
            cost = dp[(1<<n)-1][i] + abs(i - nums[0])
            if cost < minv or (cost == minv and i < last):
                minv, last = cost, i
        perm = [0]*n
        mask = (1<<n)-1
        for i in range(n-1, -1, -1):
            perm[i] = last
            pl = par[mask][last]
            mask ^= 1<<last
            last = pl
        return perm
Rust
// Omitted due to bitmask DP complexity, feasible for small n only
TypeScript
// Omitted due to bitmask DP complexity, feasible for small n only

Complexity

  • ⏰ Time complexity: O(n^2 * 2^n), feasible for n ≤ 14.
  • 🧺 Space complexity: O(n * 2^n), for the DP and parent tables

Comments