Find the Number of Ways to Place People I

Problem

You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D plane, where points[i] = [xi, yi].

Count the number of pairs of points (A, B), where

• A is on the upper left side of B, and
• there are no other points in the rectangle (or line) they make (including the border).

Return the count.

Examples

Example 1

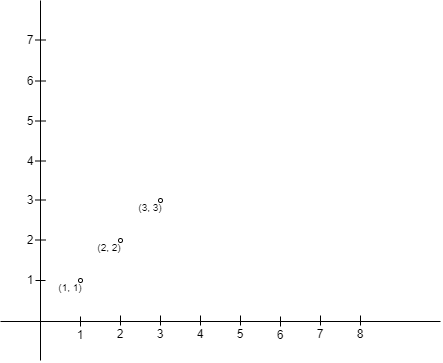
Input: points = [[1,1],[2,2],[3,3]]
Output: 0
Explanation:
There is no way to choose `A` and `B` so `A` is on the upper left side of `B`.

Example 2

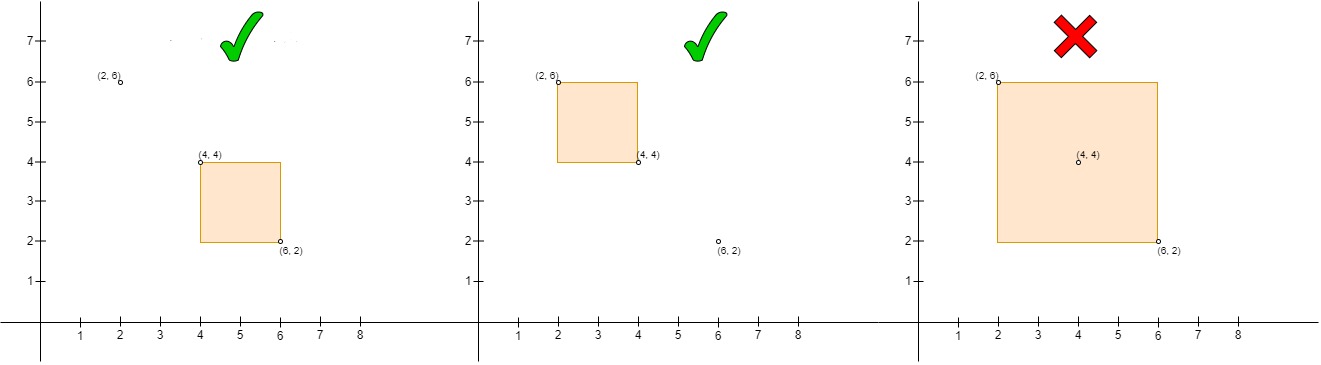
Input: points = [[6,2],[4,4],[2,6]]
Output: 2
Explanation:
  * The left one is the pair `(points[1], points[0])`, where `points[1]` is on the upper left side of `points[0]` and the rectangle is empty.
  * The middle one is the pair `(points[2], points[1])`, same as the left one it is a valid pair.
  * The right one is the pair `(points[2], points[0])`, where `points[2]` is on the upper left side of `points[0]`, but `points[1]` is inside the rectangle so it's not a valid pair.

Example 3

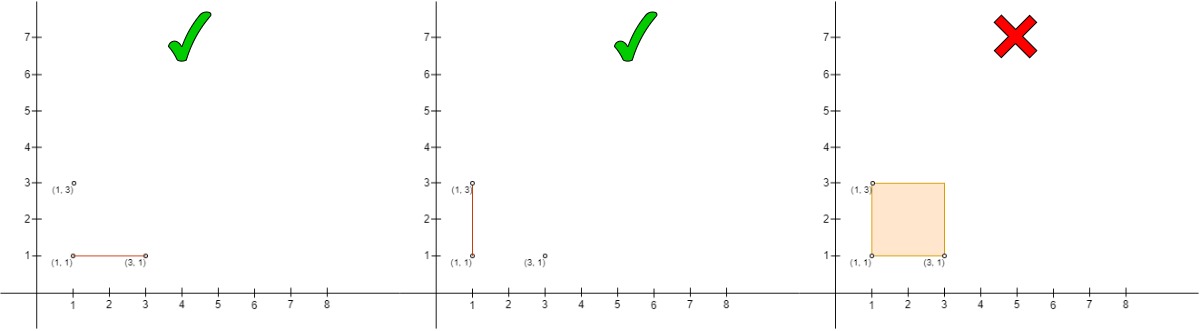
Input: points = [[3,1],[1,3],[1,1]]
Output: 2
Explanation:
  * The left one is the pair `(points[2], points[0])`, where `points[2]` is on the upper left side of `points[0]` and there are no other points on the line they form. Note that it is a valid state when the two points form a line.
  * The middle one is the pair `(points[1], points[2])`, it is a valid pair same as the left one.
  * The right one is the pair `(points[1], points[0])`, it is not a valid pair as `points[2]` is on the border of the rectangle.

Constraints

• 2 <= n <= 50
• points[i].length == 2
• 0 <= points[i][0], points[i][1] <= 50
• All points[i] are distinct.

Solution

Method 1 – Brute Force Rectangle Check

Intuition

We want to count pairs (A, B) such that A is strictly upper-left of B and there are no other points inside or on the rectangle defined by A and B. By sorting points and using a 2D Fenwick Tree, we can efficiently count the number of valid pairs by processing points in order and querying for emptiness.

Approach

1. Sort all points by x ascending, then y ascending.
2. For each point B (in sorted order):
   • For each point A before B, if A.x < B.x and A.y > B.y, check if there are no other points in the rectangle (A.x, B.x) x (B.y, A.y).
   • Use a 2D Fenwick Tree to keep track of points already processed.
   • For each B, query the number of points in the rectangle (A.x+1, B.x-1) x (B.y+1, A.y-1). If zero, count the pair.
3. Return the total count.

Code

C++

class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {
        int n = points.size();
        sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) {
            if (a[0] != b[0]) return a[0] < b[0];
            return a[1] > b[1];
        });
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            auto& first = points[i];
            for (int j = i + 1; j < n; ++j) {
                auto& second = points[j];
                if (first[0] > second[0] || first[1] < second[1]) continue;
                bool valid = true;
                for (int k = i + 1; k < j; ++k) {
                    auto& third = points[k];
                    if (first[0] <= third[0] && third[0] <= second[0] &&
                        first[1] >= third[1] && third[1] >= second[1]) {
                        valid = false;
                        break;
                    }
                }
                if (valid) ans++;
            }
        }
        return ans;
    }
};

Go

import "sort"
func numberOfPairs(points [][]int) int {
    n := len(points)
    sort.Slice(points, func(i, j int) bool {
        if points[i][0] != points[j][0] {
            return points[i][0] < points[j][0]
        }
        return points[i][1] > points[j][1]
    })
    ans := 0
    for i := 0; i < n; i++ {
        first := points[i]
        for j := i + 1; j < n; j++ {
            second := points[j]
            if first[0] > second[0] || first[1] < second[1] {
                continue
            }
            valid := true
            for k := i + 1; k < j; k++ {
                third := points[k]
                if first[0] <= third[0] && third[0] <= second[0] &&
                    first[1] >= third[1] && third[1] >= second[1] {
                    valid = false
                    break
                }
            }
            if valid {
                ans++
            }
        }
    }
    return ans
}

Java

class Solution {
    public int numberOfPairs(int[][] points) {
        int n = points.length;
        Arrays.sort(points, (a,b) ->{
            if (a[0] != b[0]){
                return a[0]-b[0];
            }
            return b[1]-a[1];
        });
        int ans = 0;
        for (int i=0;i<n;i++){
            int[] first = points[i];
            for (int j=i+1;j<n;j++){
                int[] second = points[j];
                if (first[0] > second[0] || first[1] < second[1]){
                    continue;
                }
                boolean valid = true;
                for (int k=i+1;k<j;k++){
                    int[] third = points[k];
                    if (first[0]<=third[0] && third[0]<=second[0] && first[1]>=third[1] && third[1]>=second[1]){
                        valid = false;
                        break;
                    }
                }
                if (valid){
                    ans++;
                }
            }
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun numberOfPairs(points: Array<IntArray>): Int {
        val n = points.size
        points.sortWith(compareBy({ it[0] }, { -it[1] }))
        var ans = 0
        for (i in 0 until n) {
            val first = points[i]
            for (j in i + 1 until n) {
                val second = points[j]
                if (first[0] > second[0] || first[1] < second[1]) continue
                var valid = true
                for (k in i + 1 until j) {
                    val third = points[k]
                    if (first[0] <= third[0] && third[0] <= second[0] &&
                        first[1] >= third[1] && third[1] >= second[1]) {
                        valid = false
                        break
                    }
                }
                if (valid) ans++
            }
        }
        return ans
    }
}

Python

class Solution:
    def numberOfPairs(self, points: list[list[int]]) -> int:
        n = len(points)
        points.sort(key=lambda x: (x[0], -x[1]))
        ans = 0
        for i in range(n):
            first = points[i]
            for j in range(i+1, n):
                second = points[j]
                if first[0] > second[0] or first[1] < second[1]:
                    continue
                valid = True
                for k in range(i+1, j):
                    third = points[k]
                    if first[0] <= third[0] <= second[0] and first[1] >= third[1] >= second[1]:
                        valid = False
                        break
                if valid:
                    ans += 1
        return ans

Rust

impl Solution {
    pub fn number_of_pairs(points: Vec<Vec<i32>>) -> i32 {
        let mut pts = points;
        pts.sort_by(|a, b| if a[0] != b[0] { a[0].cmp(&b[0]) } else { b[1].cmp(&a[1]) });
        let n = pts.len();
        let mut ans = 0;
        for i in 0..n {
            let first = &pts[i];
            for j in (i+1)..n {
                let second = &pts[j];
                if first[0] > second[0] || first[1] < second[1] { continue; }
                let mut valid = true;
                for k in (i+1)..j {
                    let third = &pts[k];
                    if first[0] <= third[0] && third[0] <= second[0] &&
                        first[1] >= third[1] && third[1] >= second[1] {
                        valid = false;
                        break;
                    }
                }
                if valid { ans += 1; }
            }
        }
        ans
    }
}

TypeScript

class Solution {
    numberOfPairs(points: number[][]): number {
        points.sort((a, b) => a[0] - b[0] || b[1] - a[1]);
        const n = points.length;
        let ans = 0;
        for (let i = 0; i < n; ++i) {
            const first = points[i];
            for (let j = i + 1; j < n; ++j) {
                const second = points[j];
                if (first[0] > second[0] || first[1] < second[1]) continue;
                let valid = true;
                for (let k = i + 1; k < j; ++k) {
                    const third = points[k];
                    if (first[0] <= third[0] && third[0] <= second[0] &&
                        first[1] >= third[1] && third[1] >= second[1]) {
                        valid = false;
                        break;
                    }
                }
                if (valid) ans++;
            }
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n^3) — For each pair, we may check all other points.
• 🧺 Space complexity: O(1) — Only a few variables for counting and iteration.