Find the Winner of the Circular Game

Problem

There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the ith friend brings you to the (i+1)th friend for 1 <= i < n, and moving clockwise from the nth friend brings you to the 1st friend.

The rules of the game are as follows:

1. Start at the 1st friend.
2. Count the next k friends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once.
3. The last friend you counted leaves the circle and loses the game.
4. If there is still more than one friend in the circle, go back to step 2 starting from the friend immediately clockwise of the friend who just lost and repeat.
5. Else, the last friend in the circle wins the game.

Given the number of friends, n, and an integer k, return the winner of the game.

Josephus circle

This is also called Josephus circle:

N people have decided to elect a leader by arranging themselves in a circle and eliminating every Mth person around the circle, closing ranks as each person drops out. Find which person will be the last one remaining (with rank 1).

Examples

Example 1:

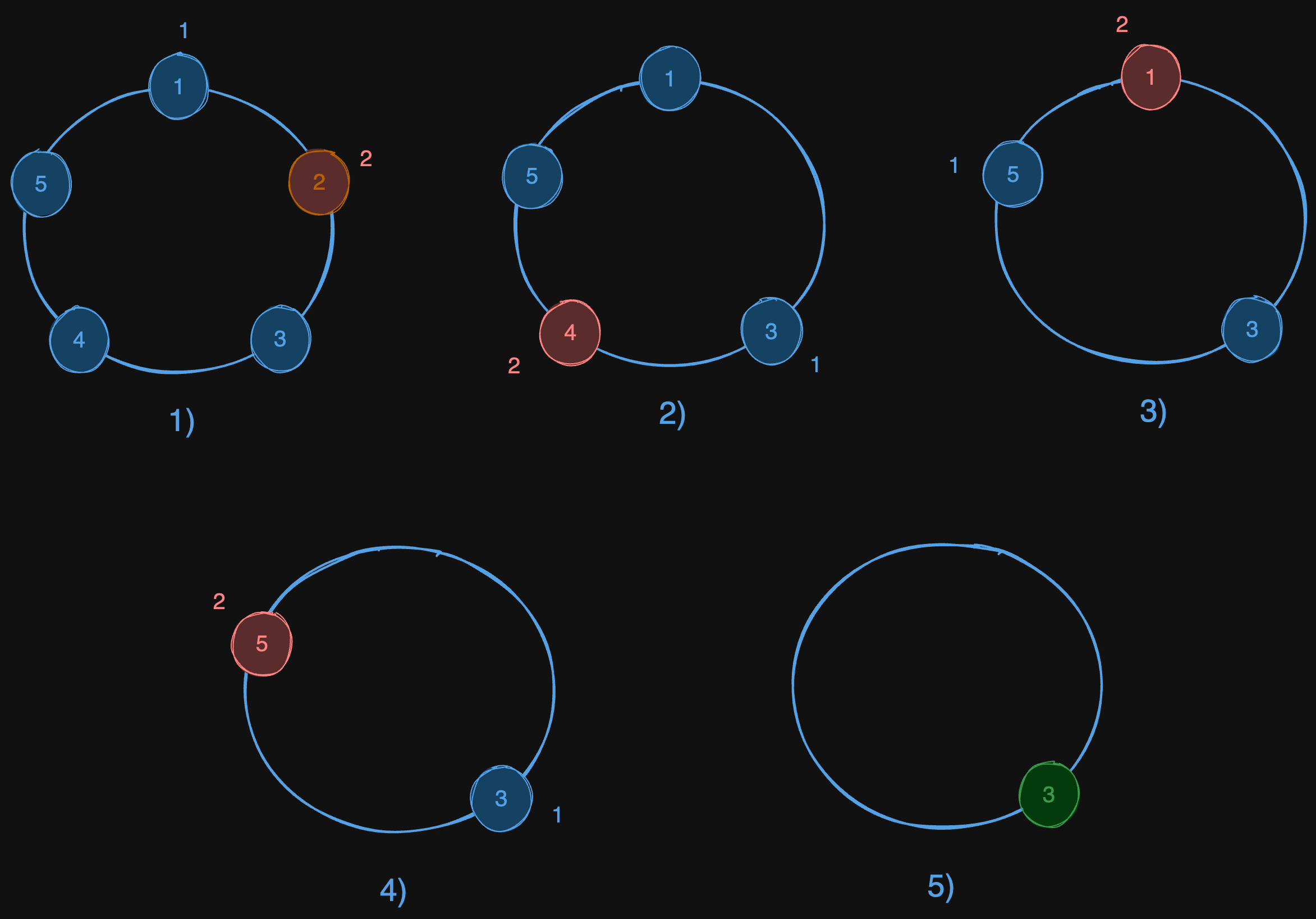
Input: n = 5, k = 2
Output: 3
Explanation: Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.

Example 2:

Input: n = 6, k = 5
Output: 1
Explanation: The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.

Solution

Method 1 - Brute Force

We can do following:

1. Use a list to represent the friends sitting in a circle.
2. Use a loop to simulate the process of eliminating every kth friend until only one friend remains.
   1. Calculate the index of the next friend to be eliminated using (currIdx + k - 1) % friends.size(). This ensures the count wraps around the circle.
   2. Remove the friend at currIdx from the list.

Code

Java

public class Solution {

	public int findTheWinner(int n, int k) {
		List<Integer> friends = new ArrayList<>();
		for (int i = 1; i <= n; i++) {
			friends.add(i);
		}

		int currIdx = 0; // Start from the 1st friend

		while (friends.size() > 1) {
			// Compute the index of the friend to be removed
			currIdx = (currIdx + k - 1) % friends.size();
			// Remove that friend
			friends.remove(currIdx);
		}

		// The last remaining friend is the winner
		return friends.get(0);
	}
}

Complexity

• ⏰ Time complexity: O(n^2), where n is number of friends.
  • Adding the friends take O(n) time
  • Now, we remove n - 1 friends from list, and removing 1 friend from list by value takes O(n). So, it should be O((n-1)*n) ⇨ O(n^2).
• 🧺 Space complexity: O(n) for storing n friends

Method 2 - Using Queue

Instead of using list, we use the queue to store the friends.

1. Use a queue to represent the friends sitting in a circle.
2. Now, to eliminate n - 1 friends, we can run the loop till queue size is 1, OR run loop n - 1
   1. Now, each time we start from first friend, and count k. We send k - 1 friends to the end of queue
   2. But kth friend will eliminated from list

[!NOTE] Note For the interview purpose, this method may not be required, until it is asked as a mathematical problem.

Here is the video explanation: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/0i9TmsxVQwg" frameborder="0" allowfullscreen></iframe></div>

Dry Run

Initialization
1 => 2 => 3 => 4 => 5

First Round
Move 1 to the end:
2 => 3 => 4 => 5 => 1
Remove the node at the current step, which is k:
3 => 4 => 5 => 1
Second Round
Move 3 to the end:
4 => 5 => 1 => 3
Remove 4:
5 => 1 => 3
Third Round
Move 5 to the end:
1 => 3 => 5
Remove 1:
3 => 5
Fourth Round
Move 3 to the end:
5 => 3
Remove 5:
3

Code

Java

class Solution {

	public int findTheWinner(int n, int k) {
		Queue<Integer> friends = new LinkedList<>();

		for (int i = 1; i <= n; i++) {
			friends.add(i);
		}

		for (int i = 1; i <= (n - 1); i++) {
			for (int j = 1; j < k; j++) {
				friends.add(friends.poll()); // simulate counting
			}

			friends.poll(); // Eliminate the kth friend
		}

		// Return the last friend remaining
		return friends.poll();
	}
}

Complexity

• ⏰ Time complexity: O(n*k)
  • Adding the friends take O(n) time
  • Then, we run elimination round n - 1 times, for k friends which takes O(n*k)
• 🧺 Space complexity: O(n)

Method 3 - Mathematics and recursion

Lets convert it to recursive function. Let's assume we have f(n,k) which will gives us one remaining after nth turn in a group of nth people if we count k person at each turn. Lets assume 0-based index.

Then, the base case is n = 1 - If there is only one person left, the winner's index is 0 (since 0-based index).

f(1, k) = 0

For generic n:

f(n,k) = (f(n-1, k)+k) % n

Our answer will be, as this is 1-based output.

g(n, k) = f(n, k) + 1;

Dry Run

We start with g(5, 2) = f(5, 2) + 1.

f(5,2) calls f(4,2) calls f(3,2) calls f(2,2) calls f(1,2).

Now, f(1,2) returns 0.

We can unwind the recursion stack now:

f(2,2) = (f(1,2) + k) % n = (0 + 2) % 2 = 0
f(3,2) = (f(2,2) + k) % n = (0 + 2) % 3 = 2
f(4,2) = (f(3,2) + k) % n = (2 + 2) % 4 = 0
f(5,2) = (f(4,2) + k) % n = (0 + 2) % 5 = 2

Now, we adjust for 1-based indexing:

g(5,2) = f(5,2) + 1 = 2 + 1 = 3

Code

Java

class Solution {
    public int findTheWinner(int n, int k) {
        return findTheWinner0Based(n, k)+1;
    }
    
    public int findTheWinner0Based(int n, int k) {
        if(n == 1) {
            return 0;
        } else {
            return (findTheWinner0Based(n - 1, k) + k) % n;
        }
    }
}

Complexity

• ⏰ Time complexity: O(n)
• 🧺 Space complexity: O(n) for using recursion stack

Method 4 - Mathematics and iterative

Code

Java

class Solution {
    public int findTheWinner(int n, int k) {
        int idx = 0;
        for(int i=1; i<=n; i++) {
            idx = (idx + k) % i;
        }
        return idx + 1;
    }
}

Complexity

• ⏰ Time complexity: O(n)
• 🧺 Space complexity: O(1)