Finding the Number of Visible Mountains

Problem

You are given a 0-indexed 2D integer array peaks where peaks[i] = [xi, yi] states that mountain i has a peak at coordinates (xi, yi). A mountain can be described as a right-angled isosceles triangle, with its base along the x-axis and a right angle at its peak. More formally, the gradients of ascending and descending the mountain are 1 and -1 respectively.

A mountain is considered visible if its peak does not lie within another mountain (including the border of other mountains).

Return the number of visible mountains.

Examples

Example 1:

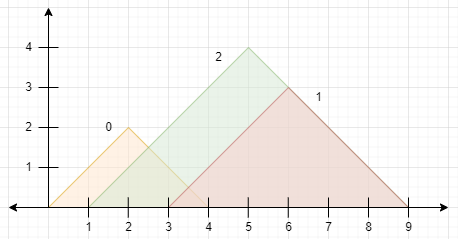
Input: peaks = [[2,2],[6,3],[5,4]]
Output: 2
Explanation: The diagram above shows the mountains.
- Mountain 0 is visible since its peak does not lie within another mountain or its sides.
- Mountain 1 is not visible since its peak lies within the side of mountain 2.
- Mountain 2 is visible since its peak does not lie within another mountain or its sides.
There are 2 mountains that are visible.

Example 2:

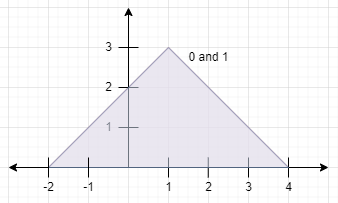
Input: peaks = [[1,3],[1,3]]
Output: 0
Explanation: The diagram above shows the mountains (they completely overlap).
Both mountains are not visible since their peaks lie within each other.

Constraints:

• 1 <= peaks.length <= 10^5
• peaks[i].length == 2
• 1 <= xi, yi <= 10^5

Solution

Method 1 – Sort by Coverage and Greedy Scan

Intuition

Each mountain covers an interval [x - y, x + y]. If a mountain's interval is completely covered by another, its peak is not visible. By sorting intervals and scanning greedily, we can efficiently count visible mountains.

Approach

1. For each peak [x, y], compute its interval [x - y, x + y].
2. Sort all intervals by left endpoint ascending, and for ties, by right endpoint descending.
3. Scan the sorted intervals:
   • Keep track of the maximum right endpoint seen so far.
   • If the current interval's right endpoint is greater than the max so far, it's visible; otherwise, it's covered.
   • Skip duplicate intervals (if two mountains are exactly the same, both are not visible).
4. Count the number of visible mountains.

Code

C++

class Solution {
public:
    int visibleMountains(vector<vector<int>>& peaks) {
        vector<pair<int, int>> segs;
        for (auto& p : peaks) segs.emplace_back(p[0] - p[1], p[0] + p[1]);
        sort(segs.begin(), segs.end(), [](auto& a, auto& b) {
            if (a.first != b.first) return a.first < b.first;
            return a.second > b.second;
        });
        int ans = 0, maxr = -1, n = segs.size();
        for (int i = 0; i < n; ++i) {
            if (i+1 < n && segs[i] == segs[i+1]) continue;
            if (segs[i].second > maxr) {
                ans++;
                maxr = segs[i].second;
            }
        }
        return ans;
    }
};

Go

func visibleMountains(peaks [][]int) int {
    n := len(peaks)
    segs := make([][2]int, n)
    for i, p := range peaks {
        segs[i] = [2]int{p[0] - p[1], p[0] + p[1]}
    }
    sort.Slice(segs, func(i, j int) bool {
        if segs[i][0] != segs[j][0] { return segs[i][0] < segs[j][0] }
        return segs[i][1] > segs[j][1]
    })
    ans, maxr := 0, -1
    for i := 0; i < n; i++ {
        if i+1 < n && segs[i] == segs[i+1] { continue }
        if segs[i][1] > maxr {
            ans++
            maxr = segs[i][1]
        }
    }
    return ans
}

Java

import java.util.*;
class Solution {
    public int visibleMountains(int[][] peaks) {
        int n = peaks.length;
        int[][] segs = new int[n][2];
        for (int i = 0; i < n; i++) {
            segs[i][0] = peaks[i][0] - peaks[i][1];
            segs[i][1] = peaks[i][0] + peaks[i][1];
        }
        Arrays.sort(segs, (a, b) -> a[0] != b[0] ? a[0] - b[0] : b[1] - a[1]);
        int ans = 0, maxr = -1;
        for (int i = 0; i < n; i++) {
            if (i+1 < n && segs[i][0] == segs[i+1][0] && segs[i][1] == segs[i+1][1]) continue;
            if (segs[i][1] > maxr) {
                ans++;
                maxr = segs[i][1];
            }
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun visibleMountains(peaks: Array<IntArray>): Int {
        val segs = peaks.map { intArrayOf(it[0] - it[1], it[0] + it[1]) }.toTypedArray()
        segs.sortWith(compareBy({ it[0] }, { -it[1] }))
        var ans = 0
        var maxr = -1
        for (i in segs.indices) {
            if (i+1 < segs.size && segs[i][0] == segs[i+1][0] && segs[i][1] == segs[i+1][1]) continue
            if (segs[i][1] > maxr) {
                ans++
                maxr = segs[i][1]
            }
        }
        return ans
    }
}

Python

class Solution:
    def visibleMountains(self, peaks: list[list[int]]) -> int:
        segs = sorted([(x-y, x+y) for x, y in peaks], key=lambda p: (p[0], -p[1]))
        ans, maxr, n = 0, -1, len(segs)
        i = 0
        while i < n:
            j = i
            while j+1 < n and segs[j+1] == segs[i]:
                j += 1
            if segs[i][1] > maxr:
                ans += 1
                maxr = segs[i][1]
            i = j + 1
        return ans

Rust

impl Solution {
    pub fn visible_mountains(peaks: Vec<Vec<i32>>) -> i32 {
        let mut segs: Vec<(i32, i32)> = peaks.iter().map(|p| (p[0]-p[1], p[0]+p[1])).collect();
        segs.sort_by(|a, b| a.0.cmp(&b.0).then(b.1.cmp(&a.1)));
        let mut ans = 0;
        let mut maxr = -1;
        let n = segs.len();
        let mut i = 0;
        while i < n {
            let mut j = i;
            while j+1 < n && segs[j+1] == segs[i] { j += 1; }
            if segs[i].1 > maxr {
                ans += 1;
                maxr = segs[i].1;
            }
            i = j + 1;
        }
        ans
    }
}

TypeScript

class Solution {
    visibleMountains(peaks: number[][]): number {
        const segs = peaks.map(([x, y]) => [x - y, x + y]);
        segs.sort((a, b) => a[0] - b[0] || b[1] - a[1]);
        let ans = 0, maxr = -1, n = segs.length, i = 0;
        while (i < n) {
            let j = i;
            while (j+1 < n && segs[j+1][0] === segs[i][0] && segs[j+1][1] === segs[i][1]) j++;
            if (segs[i][1] > maxr) {
                ans++;
                maxr = segs[i][1];
            }
            i = j + 1;
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n log n), for sorting the intervals and a single scan.
• 🧺 Space complexity: O(n), for storing the intervals.