Frog Position After T Seconds
Problem
Given an undirected tree consisting of n vertices numbered from 1 to n.
A frog starts jumping from vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.
The edges of the undirected tree are given in the array edges, where
edges[i] = [ai, bi] means that exists an edge connecting the vertices ai
and bi.
_Return the probability that aftert seconds the frog is on the vertex
target. _Answers within 10-5 of the actual answer will be accepted.
Examples
Example 1
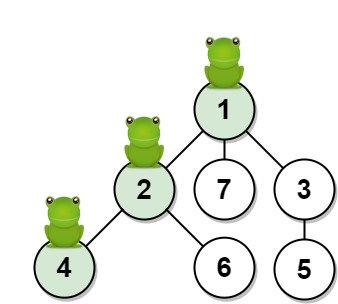
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after **second 1** and then jumping with 1/2 probability to vertex 4 after **second 2**. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.
Example 2
**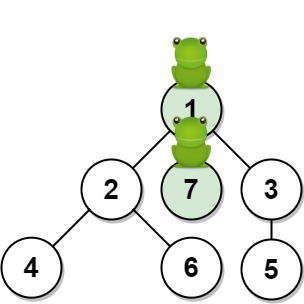**
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after **second 1**.
Constraints
1 <= n <= 100edges.length == n - 1edges[i].length == 21 <= ai, bi <= n1 <= t <= 501 <= target <= n
Solution
Method 1 – DFS with Probability Propagation
Intuition
The frog moves randomly to any unvisited neighbor at each step. We can use DFS to simulate all possible paths, propagating the probability at each step. If the frog reaches the target at time t or gets stuck (no unvisited neighbors), we record the probability.
Approach
- Build an adjacency list for the tree.
- Use DFS to traverse from node 1, keeping track of:
- The current node, time, and probability.
- Mark nodes as visited to avoid revisiting.
- At each node:
- If time equals
tor no unvisited neighbors, check if at target and return probability if so. - Otherwise, for each unvisited neighbor, recursively call DFS with incremented time and divided probability.
- If time equals
- Return the total probability of being at the target at time
t.
Code
C++
class Solution {
public:
double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
vector<vector<int>> g(n + 1);
for (auto& e : edges) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vector<bool> vis(n + 1, false);
return dfs(1, 0, 1.0, t, target, g, vis);
}
double dfs(int u, int time, double prob, int t, int target, vector<vector<int>>& g, vector<bool>& vis) {
vis[u] = true;
int cnt = 0;
for (int v : g[u]) if (!vis[v]) cnt++;
if (time == t || cnt == 0) return u == target ? prob : 0.0;
double ans = 0.0;
for (int v : g[u]) {
if (!vis[v]) {
ans += dfs(v, time + 1, prob / cnt, t, target, g, vis);
}
}
return ans;
}
};
Go
type Solution struct{}
func (Solution) frogPosition(n int, edges [][]int, t int, target int) float64 {
g := make([][]int, n+1)
for _, e := range edges {
g[e[0]] = append(g[e[0]], e[1])
g[e[1]] = append(g[e[1]], e[0])
}
vis := make([]bool, n+1)
var dfs func(u, time int, prob float64) float64
dfs = func(u, time int, prob float64) float64 {
vis[u] = true
cnt := 0
for _, v := range g[u] {
if !vis[v] { cnt++ }
}
if time == t || cnt == 0 {
if u == target { return prob }
return 0
}
ans := 0.0
for _, v := range g[u] {
if !vis[v] {
ans += dfs(v, time+1, prob/float64(cnt))
}
}
return ans
}
return dfs(1, 0, 1.0)
}
Java
class Solution {
public double frogPosition(int n, int[][] edges, int t, int target) {
List<Integer>[] g = new List[n + 1];
for (int i = 1; i <= n; i++) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(e[1]);
g[e[1]].add(e[0]);
}
boolean[] vis = new boolean[n + 1];
return dfs(1, 0, 1.0, t, target, g, vis);
}
double dfs(int u, int time, double prob, int t, int target, List<Integer>[] g, boolean[] vis) {
vis[u] = true;
int cnt = 0;
for (int v : g[u]) if (!vis[v]) cnt++;
if (time == t || cnt == 0) return u == target ? prob : 0.0;
double ans = 0.0;
for (int v : g[u]) {
if (!vis[v]) {
ans += dfs(v, time + 1, prob / cnt, t, target, g, vis);
}
}
return ans;
}
}
Kotlin
class Solution {
fun frogPosition(n: Int, edges: Array<IntArray>, t: Int, target: Int): Double {
val g = Array(n + 1) { mutableListOf<Int>() }
for (e in edges) {
g[e[0]].add(e[1])
g[e[1]].add(e[0])
}
val vis = BooleanArray(n + 1)
fun dfs(u: Int, time: Int, prob: Double): Double {
vis[u] = true
val cnt = g[u].count { !vis[it] }
if (time == t || cnt == 0) return if (u == target) prob else 0.0
var ans = 0.0
for (v in g[u]) {
if (!vis[v]) {
ans += dfs(v, time + 1, prob / cnt)
}
}
return ans
}
return dfs(1, 0, 1.0)
}
}
Python
class Solution:
def frogPosition(self, n: int, edges: list[list[int]], t: int, target: int) -> float:
from collections import defaultdict
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
vis = [False] * (n + 1)
def dfs(u: int, time: int, prob: float) -> float:
vis[u] = True
cnt = sum(not vis[v] for v in g[u])
if time == t or cnt == 0:
return prob if u == target else 0.0
ans = 0.0
for v in g[u]:
if not vis[v]:
ans += dfs(v, time + 1, prob / cnt)
return ans
return dfs(1, 0, 1.0)
Rust
impl Solution {
pub fn frog_position(n: i32, edges: Vec<Vec<i32>>, t: i32, target: i32) -> f64 {
use std::collections::VecDeque;
let n = n as usize;
let mut g = vec![vec![]; n + 1];
for e in &edges {
g[e[0] as usize].push(e[1] as usize);
g[e[1] as usize].push(e[0] as usize);
}
let mut vis = vec![false; n + 1];
fn dfs(u: usize, time: i32, prob: f64, t: i32, target: usize, g: &Vec<Vec<usize>>, vis: &mut Vec<bool>) -> f64 {
vis[u] = true;
let cnt = g[u].iter().filter(|&&v| !vis[v]).count();
if time == t || cnt == 0 {
return if u == target { prob } else { 0.0 };
}
let mut ans = 0.0;
for &v in &g[u] {
if !vis[v] {
ans += dfs(v, time + 1, prob / cnt as f64, t, target, g, vis);
}
}
ans
}
dfs(1, 0, 1.0, t, target as usize, &g, &mut vis)
}
}
TypeScript
class Solution {
frogPosition(n: number, edges: number[][], t: number, target: number): number {
const g: number[][] = Array.from({length: n + 1}, () => []);
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
const vis: boolean[] = Array(n + 1).fill(false);
function dfs(u: number, time: number, prob: number): number {
vis[u] = true;
const cnt = g[u].filter(v => !vis[v]).length;
if (time === t || cnt === 0) return u === target ? prob : 0.0;
let ans = 0.0;
for (const v of g[u]) {
if (!vis[v]) {
ans += dfs(v, time + 1, prob / cnt);
}
}
return ans;
}
return dfs(1, 0, 1.0);
}
}
Complexity
- ⏰ Time complexity:
O(n), since each node and edge is visited once in DFS. - 🧺 Space complexity:
O(n), for the adjacency list and visited array.