problemhardalgorithmsleetcode-1537leetcode 1537leetcode1537

Get the Maximum Score

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given two sorted arrays of distinct integers nums1 and nums2.

A valid __** path** is defined as follows:

  • Choose array nums1 or nums2 to traverse (from index-0).
  • Traverse the current array from left to right.
  • If you are reading any value that is present in nums1 and nums2 you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).

The score is defined as the sum of unique values in a valid path.

Return the maximum score you can obtain of all possiblevalid paths. Since the answer may be too large, return it modulo 10^9 + 7.

Examples

Example 1


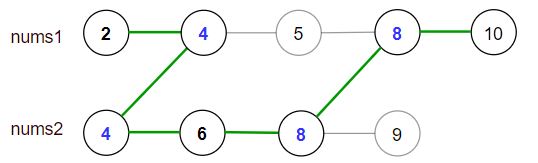
![](https://assets.leetcode.com/uploads/2020/07/16/sample_1_1893.png)

Input: nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
Output: 30
Explanation: Valid paths:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],  (starting from nums1)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10]    (starting from nums2)
The maximum is obtained with the path in green **[2,4,6,8,10]**.

Example 2

Input: nums1 = [1,3,5,7,9], nums2 = [3,5,100]
Output: 109
Explanation: Maximum sum is obtained with the path **[1,3,5,100]**.

Example 3

Input: nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
Output: 40
Explanation: There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path [6,7,8,9,10].

Constraints

  • 1 <= nums1.length, nums2.length <= 10^5
  • 1 <= nums1[i], nums2[i] <= 10^7
  • nums1 and nums2 are strictly increasing.

Solution

Method 1 – Two Pointers with Path Sums

Intuition

Since both arrays are sorted and strictly increasing, we can use two pointers to traverse both arrays. At each common element, we can choose to switch arrays, so we keep track of the sum along both paths and always take the maximum sum at each intersection.

Approach

  1. Initialize two pointers i and j for nums1 and nums2.
  2. Maintain two running sums sum1 and sum2 for the current path in each array.
  3. Traverse both arrays:
    • If nums1[i] < nums2[j], add nums1[i] to sum1 and move i.
    • If nums1[i] > nums2[j], add nums2[j] to sum2 and move j.
    • If nums1[i] == nums2[j], add the max of sum1 and sum2 plus the common value to the answer, reset both sums to 0, and move both pointers.
  4. After the loop, add the remaining sums from both arrays to the answer.
  5. Return the answer modulo 10^9 + 7.

Code

C++
class Solution {
public:
    int maxSum(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size(), m = nums2.size();
        int i = 0, j = 0;
        long sum1 = 0, sum2 = 0, ans = 0, mod = 1e9 + 7;
        while (i < n && j < m) {
            if (nums1[i] < nums2[j]) sum1 += nums1[i++];
            else if (nums1[i] > nums2[j]) sum2 += nums2[j++];
            else {
                ans += max(sum1, sum2) + nums1[i];
                sum1 = sum2 = 0;
                i++; j++;
            }
        }
        while (i < n) sum1 += nums1[i++];
        while (j < m) sum2 += nums2[j++];
        ans += max(sum1, sum2);
        return ans % mod;
    }
};
Go
func maxSum(nums1 []int, nums2 []int) int {
    i, j := 0, 0
    sum1, sum2, ans := 0, 0, 0
    mod := int(1e9 + 7)
    for i < len(nums1) && j < len(nums2) {
        if nums1[i] < nums2[j] {
            sum1 += nums1[i]
            i++
        } else if nums1[i] > nums2[j] {
            sum2 += nums2[j]
            j++
        } else {
            ans += max(sum1, sum2) + nums1[i]
            sum1, sum2 = 0, 0
            i++
            j++
        }
    }
    for i < len(nums1) {
        sum1 += nums1[i]
        i++
    }
    for j < len(nums2) {
        sum2 += nums2[j]
        j++
    }
    ans += max(sum1, sum2)
    return ans % mod
}
func max(a, b int) int {
    if a > b { return a }
    return b
}
Java
class Solution {
    public int maxSum(int[] nums1, int[] nums2) {
        int n = nums1.length, m = nums2.length;
        int i = 0, j = 0;
        long sum1 = 0, sum2 = 0, ans = 0, mod = 1_000_000_007;
        while (i < n && j < m) {
            if (nums1[i] < nums2[j]) sum1 += nums1[i++];
            else if (nums1[i] > nums2[j]) sum2 += nums2[j++];
            else {
                ans += Math.max(sum1, sum2) + nums1[i];
                sum1 = sum2 = 0;
                i++; j++;
            }
        }
        while (i < n) sum1 += nums1[i++];
        while (j < m) sum2 += nums2[j++];
        ans += Math.max(sum1, sum2);
        return (int)(ans % mod);
    }
}
Kotlin
class Solution {
    fun maxSum(nums1: IntArray, nums2: IntArray): Int {
        var i = 0
        var j = 0
        var sum1 = 0L
        var sum2 = 0L
        var ans = 0L
        val mod = 1_000_000_007L
        while (i < nums1.size && j < nums2.size) {
            when {
                nums1[i] < nums2[j] -> sum1 += nums1[i++]
                nums1[i] > nums2[j] -> sum2 += nums2[j++]
                else -> {
                    ans += maxOf(sum1, sum2) + nums1[i]
                    sum1 = 0
                    sum2 = 0
                    i++
                    j++
                }
            }
        }
        while (i < nums1.size) sum1 += nums1[i++]
        while (j < nums2.size) sum2 += nums2[j++]
        ans += maxOf(sum1, sum2)
        return (ans % mod).toInt()
    }
}
Python
class Solution:
    def maxSum(self, nums1: list[int], nums2: list[int]) -> int:
        i = j = 0
        sum1 = sum2 = ans = 0
        mod = 10**9 + 7
        n, m = len(nums1), len(nums2)
        while i < n and j < m:
            if nums1[i] < nums2[j]:
                sum1 += nums1[i]
                i += 1
            elif nums1[i] > nums2[j]:
                sum2 += nums2[j]
                j += 1
            else:
                ans += max(sum1, sum2) + nums1[i]
                sum1 = sum2 = 0
                i += 1
                j += 1
        while i < n:
            sum1 += nums1[i]
            i += 1
        while j < m:
            sum2 += nums2[j]
            j += 1
        ans += max(sum1, sum2)
        return ans % mod
Rust
impl Solution {
    pub fn max_sum(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
        let (mut i, mut j) = (0, 0);
        let (mut sum1, mut sum2, mut ans) = (0i64, 0i64, 0i64);
        let n = nums1.len();
        let m = nums2.len();
        let modv = 1_000_000_007;
        while i < n && j < m {
            if nums1[i] < nums2[j] {
                sum1 += nums1[i] as i64;
                i += 1;
            } else if nums1[i] > nums2[j] {
                sum2 += nums2[j] as i64;
                j += 1;
            } else {
                ans += sum1.max(sum2) + nums1[i] as i64;
                sum1 = 0;
                sum2 = 0;
                i += 1;
                j += 1;
            }
        }
        while i < n {
            sum1 += nums1[i] as i64;
            i += 1;
        }
        while j < m {
            sum2 += nums2[j] as i64;
            j += 1;
        }
        ans += sum1.max(sum2);
        (ans % modv) as i32
    }
}
TypeScript
class Solution {
    maxSum(nums1: number[], nums2: number[]): number {
        let i = 0, j = 0;
        let sum1 = 0, sum2 = 0, ans = 0;
        const mod = 1e9 + 7;
        while (i < nums1.length && j < nums2.length) {
            if (nums1[i] < nums2[j]) sum1 += nums1[i++];
            else if (nums1[i] > nums2[j]) sum2 += nums2[j++];
            else {
                ans += Math.max(sum1, sum2) + nums1[i];
                sum1 = sum2 = 0;
                i++; j++;
            }
        }
        while (i < nums1.length) sum1 += nums1[i++];
        while (j < nums2.length) sum2 += nums2[j++];
        ans += Math.max(sum1, sum2);
        return ans % mod;
    }
}

Complexity

  • ⏰ Time complexity: O(n + m) — Each element in both arrays is visited at most once.
  • 🧺 Space complexity: O(1) — Only a constant amount of extra space is used for pointers and sums.

Comments