problemhardalgorithmsleetcode-1627leetcode 1627leetcode1627

Graph Connectivity With Threshold

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:

  • x % z == 0,
  • y % z == 0, and
  • z > threshold.

Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [ai, bi] if cities ai and bi are connected directly or indirectly. (i.e. there is some path between them).

Return an arrayanswer , whereanswer.length == queries.length andanswer[i]istrue if for theith query, there is a path betweenai andbi , oranswer[i]isfalse if there is no path.

Examples

Example 1


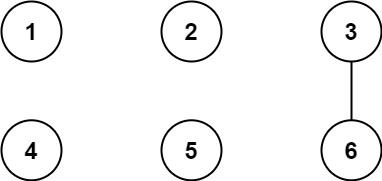
![](https://assets.leetcode.com/uploads/2020/10/09/ex1.jpg)

Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
Output: [false,false,true]
Explanation: The divisors for each number:
1:   1
2:   1, 2
3:   1, _3_
4:   1, 2, _4_
5:   1, _5_
6:   1, 2, _3_ , _6_
Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the
only ones directly connected. The result of each query:
[1,4]   1 is not connected to 4
[2,5]   2 is not connected to 5
[3,6]   3 is connected to 6 through path 3--6

Example 2


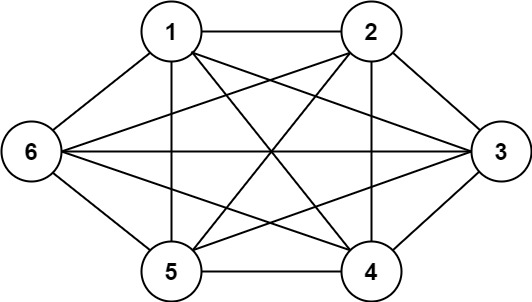
![](https://assets.leetcode.com/uploads/2020/10/10/tmp.jpg)

Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
Output: [true,true,true,true,true]
Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0,
all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.

Example 3


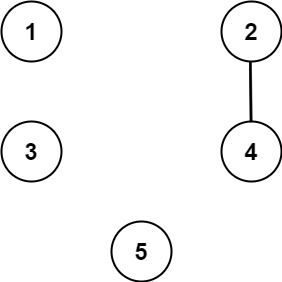
![](https://assets.leetcode.com/uploads/2020/10/17/ex3.jpg)

Input: n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
Output: [false,false,false,false,false]
Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected.
Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].

Constraints

  • 2 <= n <= 10^4
  • 0 <= threshold <= n
  • 1 <= queries.length <= 10^5
  • queries[i].length == 2
  • 1 <= ai, bi <= cities
  • ai != bi

Solution

Method 1 – Union-Find with Divisor Grouping

Intuition

Cities are connected if they share a common divisor greater than the threshold. For each divisor d > threshold, all multiples of d are directly connected. We can use Union-Find (Disjoint Set Union) to group all such cities efficiently, then answer each query by checking if two cities are in the same group.

Approach

  1. Initialize a Union-Find (DSU) structure for all cities.
  2. For each divisor d from threshold + 1 to n:
    • For each multiple m of d (from 2*d to n), union d and m.
  3. For each query [a, b], check if a and b are in the same group using DSU.
  4. Return the results for all queries.

Code

C++
class Solution {
public:
    vector<bool> areConnected(int n, int threshold, vector<vector<int>>& queries) {
        vector<int> p(n + 1);
        iota(p.begin(), p.end(), 0);
        function<int(int)> find = [&](int x) { return p[x] == x ? x : p[x] = find(p[x]); };
        for (int d = threshold + 1; d <= n; ++d) {
            for (int m = 2 * d; m <= n; m += d) {
                p[find(d)] = find(m);
            }
        }
        vector<bool> ans;
        for (auto& q : queries) {
            ans.push_back(find(q[0]) == find(q[1]));
        }
        return ans;
    }
};
Go
func areConnected(n int, threshold int, queries [][]int) []bool {
    p := make([]int, n+1)
    for i := range p { p[i] = i }
    var find func(int) int
    find = func(x int) int {
        if p[x] != x { p[x] = find(p[x]) }
        return p[x]
    }
    for d := threshold + 1; d <= n; d++ {
        for m := 2 * d; m <= n; m += d {
            p[find(d)] = find(m)
        }
    }
    ans := make([]bool, len(queries))
    for i, q := range queries {
        ans[i] = find(q[0]) == find(q[1])
    }
    return ans
}
Java
class Solution {
    public List<Boolean> areConnected(int n, int threshold, int[][] queries) {
        int[] p = new int[n + 1];
        for (int i = 0; i <= n; i++) p[i] = i;
        java.util.function.IntUnaryOperator find = new java.util.function.IntUnaryOperator() {
            public int applyAsInt(int x) { return p[x] == x ? x : (p[x] = applyAsInt(p[x])); }
        };
        for (int d = threshold + 1; d <= n; d++) {
            for (int m = 2 * d; m <= n; m += d) {
                p[find.applyAsInt(d)] = find.applyAsInt(m);
            }
        }
        List<Boolean> ans = new ArrayList<>();
        for (int[] q : queries) {
            ans.add(find.applyAsInt(q[0]) == find.applyAsInt(q[1]));
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun areConnected(n: Int, threshold: Int, queries: Array<IntArray>): List<Boolean> {
        val p = IntArray(n + 1) { it }
        fun find(x: Int): Int = if (p[x] == x) x else { p[x] = find(p[x]); p[x] }
        for (d in threshold + 1..n) {
            var m = 2 * d
            while (m <= n) {
                p[find(d)] = find(m)
                m += d
            }
        }
        return queries.map { find(it[0]) == find(it[1]) }
    }
}
Python
class Solution:
    def areConnected(self, n: int, threshold: int, queries: list[list[int]]) -> list[bool]:
        p = list(range(n + 1))
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]
        for d in range(threshold + 1, n + 1):
            for m in range(2 * d, n + 1, d):
                p[find(d)] = find(m)
        return [find(a) == find(b) for a, b in queries]
Rust
impl Solution {
    pub fn are_connected(n: i32, threshold: i32, queries: Vec<Vec<i32>>) -> Vec<bool> {
        let n = n as usize;
        let threshold = threshold as usize;
        let mut p: Vec<usize> = (0..=n).collect();
        fn find(p: &mut Vec<usize>, x: usize) -> usize {
            if p[x] != x { p[x] = find(p, p[x]); }
            p[x]
        }
        for d in threshold+1..=n {
            let mut m = 2*d;
            while m <= n {
                let pd = find(&mut p, d);
                let pm = find(&mut p, m);
                p[pd] = pm;
                m += d;
            }
        }
        queries.iter().map(|q| find(&mut p, q[0] as usize) == find(&mut p, q[1] as usize)).collect()
    }
}
TypeScript
class Solution {
    areConnected(n: number, threshold: number, queries: number[][]): boolean[] {
        const p = Array.from({length: n+1}, (_, i) => i);
        const find = (x: number): number => p[x] === x ? x : (p[x] = find(p[x]));
        for (let d = threshold + 1; d <= n; d++) {
            for (let m = 2 * d; m <= n; m += d) {
                p[find(d)] = find(m);
            }
        }
        return queries.map(([a, b]) => find(a) === find(b));
    }
}

Complexity

  • ⏰ Time complexity: O(n log n + q) — Union-Find with path compression is nearly linear, and each query is O(1).
  • 🧺 Space complexity: O(n) — For the parent array in DSU.

Comments