Guess Number Higher or Lower II
MediumUpdated: Aug 2, 2025
Practice on:
Problem
We are playing the Guessing Game. The game will work as follows:
- I pick a number between
1andn. - You guess a number.
- If you guess the right number, you win the game.
- If you guess the wrong number, then I will tell you whether the number I picked is higher or lower, and you will continue guessing.
- Every time you guess a wrong number
x, you will payxdollars. If you run out of money, you lose the game.
Given a particular n, return the minimum amount of money you need to guarantee a win regardless of what number I pick.
Examples
Example 1
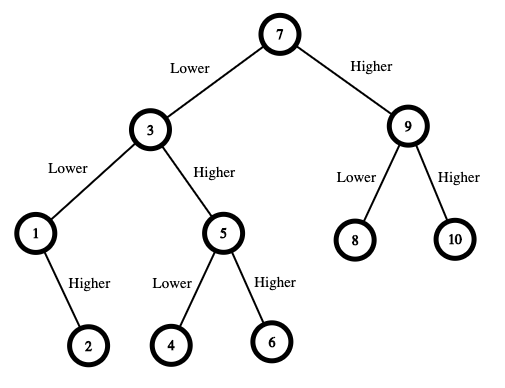
Input: n = 10
Output: 16
Explanation: The winning strategy is as follows:
- The range is [1,10]. Guess 7.
- If this is my number, your total is $0. Otherwise, you pay $7.
- If my number is higher, the range is [8,10]. Guess 9.
- If this is my number, your total is $7. Otherwise, you pay $9.
- If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
- If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
- If my number is lower, the range is [1,6]. Guess 3.
- If this is my number, your total is $7. Otherwise, you pay $3.
- If my number is higher, the range is [4,6]. Guess 5.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
- If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
- If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
- If my number is lower, the range is [1,2]. Guess 1.
- If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
Example 2
Input: n = 1
Output: 0
Explanation: There is only one possible number, so you can guess 1 and not have to pay anything.
Example 3
Input: n = 2
Output: 1
Explanation: There are two possible numbers, 1 and 2.
- Guess 1.
- If this is my number, your total is $0. Otherwise, you pay $1.
- If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.
Constraints
1 <= n <= 200
Solution
Method 1 – Dynamic Programming (Minimax)
Intuition
To guarantee a win with the minimum cost, we use dynamic programming and minimax. For each range [l, r], we try every possible guess x, and the cost is x plus the maximum cost of the two resulting subranges. We want the minimum among all possible guesses.
Approach
- Use a DP table
dp[l][r]wheredp[l][r]is the minimum cost to guarantee a win in range [l, r]. - For each range, try every possible guess x in [l, r].
- For each guess, the cost is x plus the maximum of dp[l][x-1] and dp[x+1][r].
- Fill the DP table bottom-up.
- The answer is dp[1][n].
Code
C++
class Solution {
public:
int getMoneyAmount(int n) {
vector<vector<int>> dp(n+2, vector<int>(n+2, 0));
for (int len = 2; len <= n; ++len) {
for (int l = 1; l+len-1 <= n; ++l) {
int r = l+len-1;
dp[l][r] = INT_MAX;
for (int x = l; x <= r; ++x) {
int cost = x + max(dp[l][x-1], dp[x+1][r]);
dp[l][r] = min(dp[l][r], cost);
}
}
}
return dp[1][n];
}
};
Go
func getMoneyAmount(n int) int {
dp := make([][]int, n+2)
for i := range dp {
dp[i] = make([]int, n+2)
}
for length := 2; length <= n; length++ {
for l := 1; l+length-1 <= n; l++ {
r := l+length-1
dp[l][r] = 1<<31-1
for x := l; x <= r; x++ {
cost := x + max(dp[l][x-1], dp[x+1][r])
if cost < dp[l][r] {
dp[l][r] = cost
}
}
}
}
return dp[1][n]
}
func max(a, b int) int { if a > b { return a }; return b }
Java
class Solution {
public int getMoneyAmount(int n) {
int[][] dp = new int[n+2][n+2];
for (int len = 2; len <= n; len++) {
for (int l = 1; l+len-1 <= n; l++) {
int r = l+len-1;
dp[l][r] = Integer.MAX_VALUE;
for (int x = l; x <= r; x++) {
int cost = x + Math.max(dp[l][x-1], dp[x+1][r]);
dp[l][r] = Math.min(dp[l][r], cost);
}
}
}
return dp[1][n];
}
}
Kotlin
class Solution {
fun getMoneyAmount(n: Int): Int {
val dp = Array(n+2) { IntArray(n+2) }
for (len in 2..n) {
for (l in 1..n-len+1) {
val r = l+len-1
dp[l][r] = Int.MAX_VALUE
for (x in l..r) {
val cost = x + maxOf(dp[l][x-1], dp[x+1][r])
dp[l][r] = minOf(dp[l][r], cost)
}
}
}
return dp[1][n]
}
}
Python
def getMoneyAmount(n: int) -> int:
dp = [[0]*(n+2) for _ in range(n+2)]
for length in range(2, n+1):
for l in range(1, n-length+2):
r = l+length-1
dp[l][r] = float('inf')
for x in range(l, r+1):
cost = x + max(dp[l][x-1], dp[x+1][r])
dp[l][r] = min(dp[l][r], cost)
return dp[1][n]
Rust
impl Solution {
pub fn get_money_amount(n: i32) -> i32 {
let n = n as usize;
let mut dp = vec![vec![0; n+2]; n+2];
for len in 2..=n {
for l in 1..=n-len+1 {
let r = l+len-1;
dp[l][r] = i32::MAX;
for x in l..=r {
let cost = x as i32 + dp[l][x-1].max(dp[x+1][r]);
dp[l][r] = dp[l][r].min(cost);
}
}
}
dp[1][n]
}
}
TypeScript
class Solution {
getMoneyAmount(n: number): number {
const dp: number[][] = Array.from({length: n+2}, () => Array(n+2).fill(0));
for (let len = 2; len <= n; len++) {
for (let l = 1; l+len-1 <= n; l++) {
const r = l+len-1;
dp[l][r] = Infinity;
for (let x = l; x <= r; x++) {
const cost = x + Math.max(dp[l][x-1], dp[x+1][r]);
dp[l][r] = Math.min(dp[l][r], cost);
}
}
}
return dp[1][n];
}
}
Complexity
- ⏰ Time complexity:
O(n^3), since for each range and guess, we fill the DP table. - 🧺 Space complexity:
O(n^2), for the DP table.