problemmediumalgorithmsleetcode-2773leetcode 2773leetcode2773

Height of Special Binary Tree

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a root, which is the root of a special binary tree with n nodes. The nodes of the special binary tree are numbered from 1 to n. Suppose the tree has k leaves in the following order: b1 < b2 < ... < bk.

The leaves of this tree have a special property! That is, for every leaf bi, the following conditions hold:

  • The right child of bi is bi + 1 if i < k, and b1 otherwise.
  • The left child of bi is bi - 1 if i > 1, and bk otherwise.

Return the height of the given tree.

Note: The height of a binary tree is the length of the longest path from the root to any other node.

Examples

Example 1:

Input: root = [1,2,3,null,null,4,5]
Output: 2
Explanation: The given tree is shown in the following picture. Each leaf's left child is the leaf to its left (shown with the blue edges). Each leaf's right child is the leaf to its right (shown with the red edges). We can see that the graph has a height of 2.
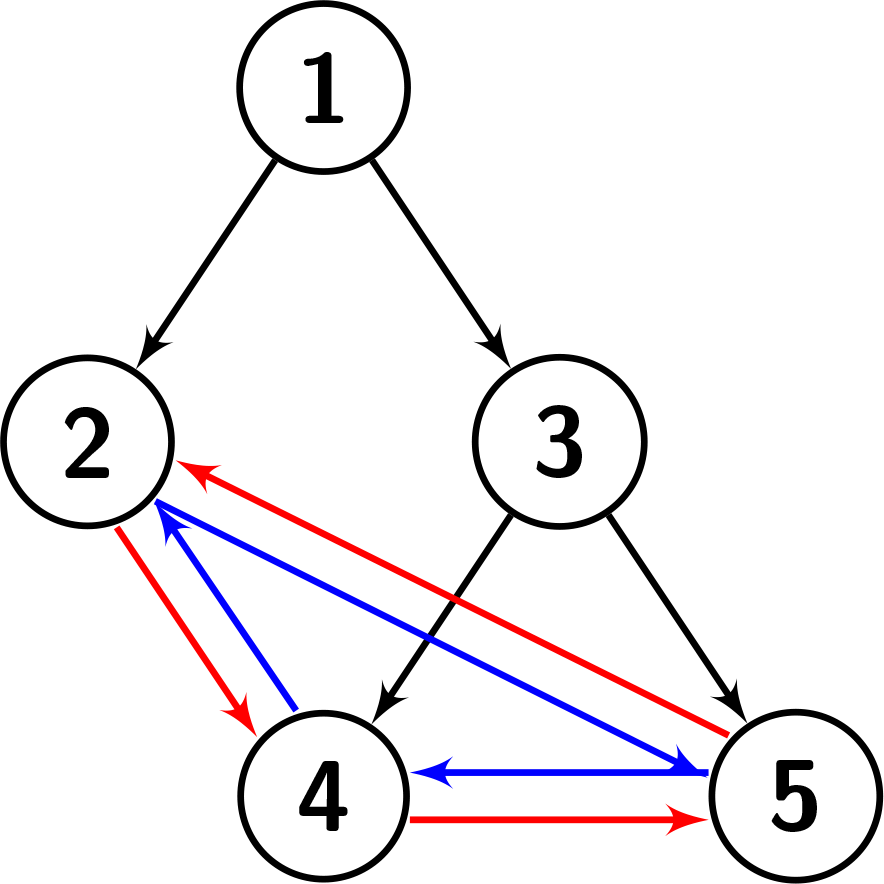
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2700-2799/2773.Height%20of%20Special%20Binary%20Tree/images/1.png)

Example 2:

Input: root = [1,2]
Output: 1
Explanation: The given tree is shown in the following picture. There is only one leaf, so it doesn't have any left or right child. We can see that the graph has a height of 1.
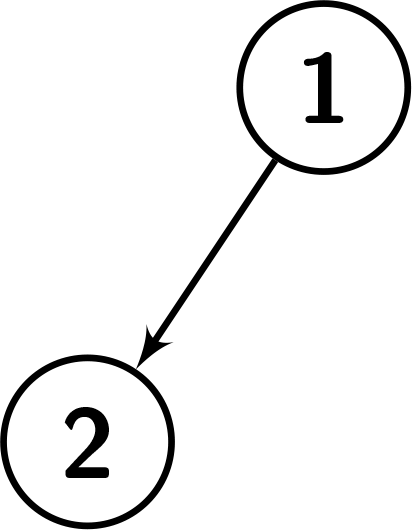
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2700-2799/2773.Height%20of%20Special%20Binary%20Tree/images/2.png)

Example 3:

Input: root = [1,2,3,null,null,4,null,5,6]
Output: 3
Explanation: The given tree is shown in the following picture. Each leaf's left child is the leaf to its left (shown with the blue edges). Each leaf's right child is the leaf to its right (shown with the red edges). We can see that the graph has a height of 3.
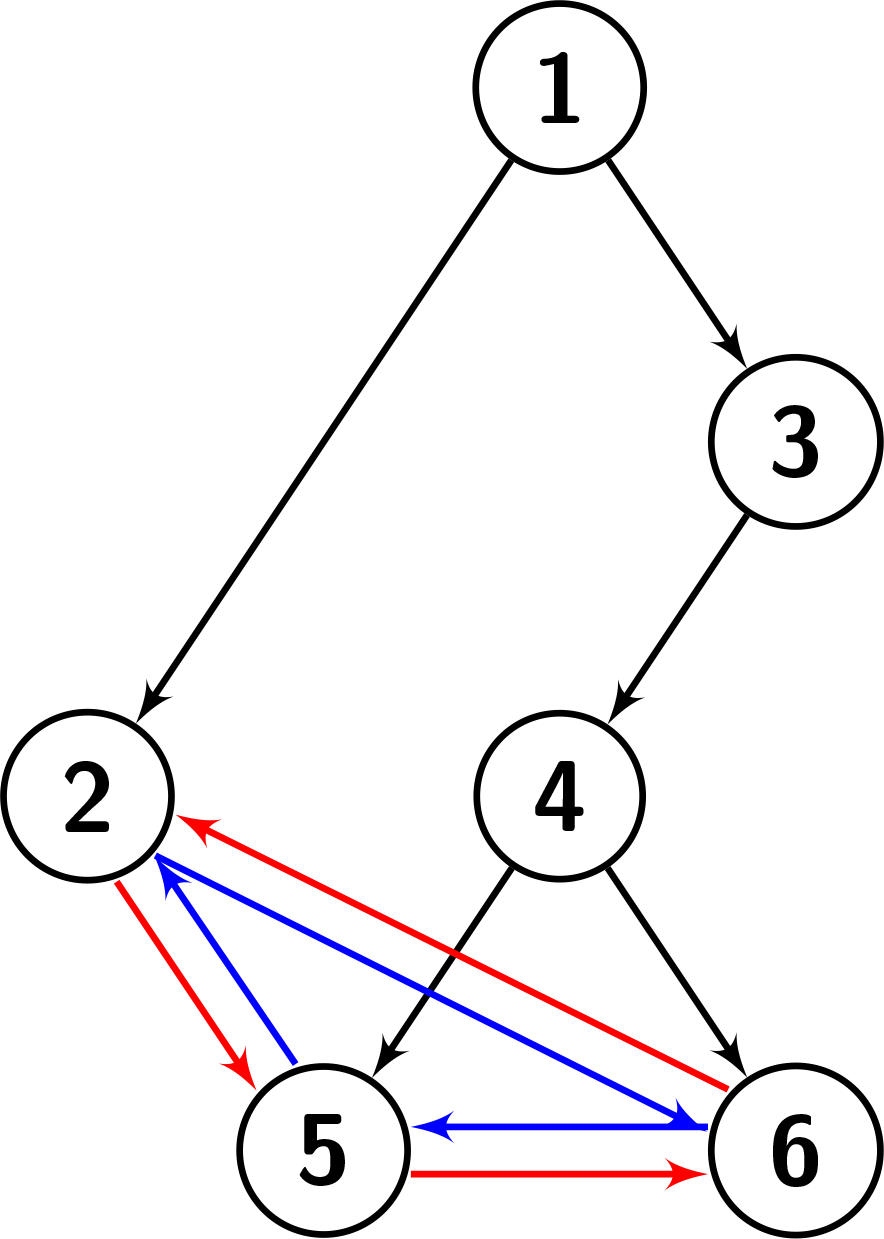
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2700-2799/2773.Height%20of%20Special%20Binary%20Tree/images/3.png)

Constraints:

  • n == number of nodes in the tree
  • 2 <= n <= 10^4
  • 1 <= node.val <= n
  • The input is generated such that each node.val is unique.

Solution

Method 1 – Depth-First Search (DFS) for Height

Intuition

The special property of the leaves does not affect the height, since the height is defined as the longest path from the root to any node, and the extra leaf connections do not create longer paths. So, we can compute the height using a standard DFS.

Approach

  1. Traverse the tree using DFS.
  2. For each node, recursively compute the height of its left and right subtrees.
  3. The height of the node is 1 plus the maximum of its left and right subtree heights.
  4. Return the height of the root.

Code

C++
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
    int heightOfTree(TreeNode* root) {
        if (!root) return -1;
        int l = heightOfTree(root->left);
        int r = heightOfTree(root->right);
        return 1 + max(l, r);
    }
};
Go
type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func heightOfTree(root *TreeNode) int {
    if root == nil {
        return -1
    }
    l := heightOfTree(root.Left)
    r := heightOfTree(root.Right)
    if l > r {
        return l + 1
    }
    return r + 1
}
Java
class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    public int heightOfTree(TreeNode root) {
        if (root == null) return -1;
        int l = heightOfTree(root.left);
        int r = heightOfTree(root.right);
        return 1 + Math.max(l, r);
    }
}
Kotlin
data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    fun heightOfTree(root: TreeNode?): Int {
        if (root == null) return -1
        val l = heightOfTree(root.left)
        val r = heightOfTree(root.right)
        return 1 + maxOf(l, r)
    }
}
Python
class TreeNode:
    def __init__(self, val: int = 0, left: 'TreeNode' = None, right: 'TreeNode' = None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def heightOfTree(self, root: TreeNode) -> int:
        if not root:
            return -1
        l = self.heightOfTree(root.left)
        r = self.heightOfTree(root.right)
        return 1 + max(l, r)
Rust
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Box<TreeNode>>,
    pub right: Option<Box<TreeNode>>,
}
impl TreeNode {
    pub fn new(val: i32) -> Self {
        TreeNode { val, left: None, right: None }
    }
}
pub struct Solution;
impl Solution {
    pub fn height_of_tree(root: Option<Box<TreeNode>>) -> i32 {
        match root {
            None => -1,
            Some(node) => {
                let l = Solution::height_of_tree(node.left);
                let r = Solution::height_of_tree(node.right);
                1 + l.max(r)
            }
        }
    }
}
TypeScript
class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = val ?? 0;
        this.left = left ?? null;
        this.right = right ?? null;
    }
}
class Solution {
    heightOfTree(root: TreeNode | null): number {
        if (!root) return -1;
        const l = this.heightOfTree(root.left);
        const r = this.heightOfTree(root.right);
        return 1 + Math.max(l, r);
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nodes, since each node is visited once.
  • 🧺 Space complexity: O(h), where h is the height of the tree, due to recursion stack.

Comments