Increment Submatrices by One
MediumUpdated: Aug 2, 2025
Practice on:
Problem
You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.
You are also given a 2D integer array query. For each query[i] = [row1i, col1i, row2i, col2i], you should do the following operation:
- Add
1to every element in the submatrix with the top left corner(row1i, col1i)and the bottom right corner(row2i, col2i). That is, add1tomat[x][y]for allrow1i <= x <= row2iandcol1i <= y <= col2i.
Return the matrix mat after performing every query.
Examples
Example 1
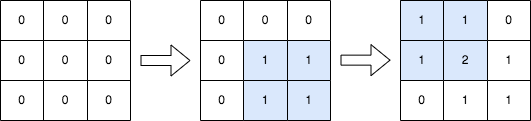
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
Example 2

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
Constraints
1 <= n <= 5001 <= queries.length <= 10^40 <= row1i <= row2i < n0 <= col1i <= col2i < n
Solution
Method 1 – 2D Prefix Sum (Imos Method)
Intuition
Directly incrementing all elements in each submatrix for every query is too slow. Instead, we use a 2D prefix sum trick (Imos method) to efficiently apply all increments, then compute the final matrix in one pass.
Approach
- Create a 2D difference matrix
diffof size (n+1) x (n+1), initialized to 0. - For each query
[r1, c1, r2, c2], update the corners ofdiffto mark the increment region:diff[r1][c1] += 1diff[r1][c2+1] -= 1diff[r2+1][c1] -= 1diff[r2+1][c2+1] += 1
- After all queries, compute the prefix sums row-wise and then column-wise to get the final matrix.
- Return the resulting matrix.
Code
C++
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
vector<vector<int>> diff(n+1, vector<int>(n+1));
for (auto& q : queries) {
int r1 = q[0], c1 = q[1], r2 = q[2], c2 = q[3];
diff[r1][c1]++;
diff[r1][c2+1]--;
diff[r2+1][c1]--;
diff[r2+1][c2+1]++;
}
vector<vector<int>> ans(n, vector<int>(n));
for (int i = 0; i < n; ++i)
for (int j = 1; j < n; ++j)
diff[i][j] += diff[i][j-1];
for (int j = 0; j < n; ++j)
for (int i = 1; i < n; ++i)
diff[i][j] += diff[i-1][j];
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
ans[i][j] = diff[i][j];
return ans;
}
Go
func rangeAddQueries(n int, queries [][]int) [][]int {
diff := make([][]int, n+1)
for i := range diff {
diff[i] = make([]int, n+1)
}
for _, q := range queries {
r1, c1, r2, c2 := q[0], q[1], q[2], q[3]
diff[r1][c1]++
diff[r1][c2+1]--
diff[r2+1][c1]--
diff[r2+1][c2+1]++
}
for i := 0; i < n; i++ {
for j := 1; j < n; j++ {
diff[i][j] += diff[i][j-1]
}
}
for j := 0; j < n; j++ {
for i := 1; i < n; i++ {
diff[i][j] += diff[i-1][j]
}
}
ans := make([][]int, n)
for i := 0; i < n; i++ {
ans[i] = make([]int, n)
for j := 0; j < n; j++ {
ans[i][j] = diff[i][j]
}
}
return ans
}
Java
class Solution {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] diff = new int[n+1][n+1];
for (int[] q : queries) {
int r1 = q[0], c1 = q[1], r2 = q[2], c2 = q[3];
diff[r1][c1]++;
diff[r1][c2+1]--;
diff[r2+1][c1]--;
diff[r2+1][c2+1]++;
}
for (int i = 0; i < n; ++i)
for (int j = 1; j < n; ++j)
diff[i][j] += diff[i][j-1];
for (int j = 0; j < n; ++j)
for (int i = 1; i < n; ++i)
diff[i][j] += diff[i-1][j];
int[][] ans = new int[n][n];
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
ans[i][j] = diff[i][j];
return ans;
}
}
Kotlin
fun rangeAddQueries(n: Int, queries: Array<IntArray>): Array<IntArray> {
val diff = Array(n+1) { IntArray(n+1) }
for (q in queries) {
val (r1, c1, r2, c2) = q
diff[r1][c1]++
diff[r1][c2+1]--
diff[r2+1][c1]--
diff[r2+1][c2+1]++
}
for (i in 0 until n)
for (j in 1 until n)
diff[i][j] += diff[i][j-1]
for (j in 0 until n)
for (i in 1 until n)
diff[i][j] += diff[i-1][j]
val ans = Array(n) { IntArray(n) }
for (i in 0 until n)
for (j in 0 until n)
ans[i][j] = diff[i][j]
return ans
}
Python
def rangeAddQueries(n: int, queries: list[list[int]]) -> list[list[int]]:
diff = [[0]*(n+1) for _ in range(n+1)]
for r1, c1, r2, c2 in queries:
diff[r1][c1] += 1
diff[r1][c2+1] -= 1
diff[r2+1][c1] -= 1
diff[r2+1][c2+1] += 1
for i in range(n):
for j in range(1, n):
diff[i][j] += diff[i][j-1]
for j in range(n):
for i in range(1, n):
diff[i][j] += diff[i-1][j]
ans = [[diff[i][j] for j in range(n)] for i in range(n)]
return ans
Rust
fn range_add_queries(n: i32, queries: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
let n = n as usize;
let mut diff = vec![vec![0; n+1]; n+1];
for q in queries {
let (r1, c1, r2, c2) = (q[0] as usize, q[1] as usize, q[2] as usize, q[3] as usize);
diff[r1][c1] += 1;
diff[r1][c2+1] -= 1;
diff[r2+1][c1] -= 1;
diff[r2+1][c2+1] += 1;
}
for i in 0..n {
for j in 1..n {
diff[i][j] += diff[i][j-1];
}
}
for j in 0..n {
for i in 1..n {
diff[i][j] += diff[i-1][j];
}
}
let mut ans = vec![vec![0; n]; n];
for i in 0..n {
for j in 0..n {
ans[i][j] = diff[i][j];
}
}
ans
}
TypeScript
function rangeAddQueries(n: number, queries: number[][]): number[][] {
const diff = Array.from({length: n+1}, () => Array(n+1).fill(0));
for (const [r1, c1, r2, c2] of queries) {
diff[r1][c1]++;
diff[r1][c2+1]--;
diff[r2+1][c1]--;
diff[r2+1][c2+1]++;
}
for (let i = 0; i < n; ++i)
for (let j = 1; j < n; ++j)
diff[i][j] += diff[i][j-1];
for (let j = 0; j < n; ++j)
for (let i = 1; i < n; ++i)
diff[i][j] += diff[i-1][j];
const ans = Array.from({length: n}, () => Array(n));
for (let i = 0; i < n; ++i)
for (let j = 0; j < n; ++j)
ans[i][j] = diff[i][j];
return ans;
}
Complexity
- ⏰ Time complexity:
O(q + n^2)— q is the number of queries, n is the matrix size. Each query is O(1), and prefix sum is O(n^2). - 🧺 Space complexity:
O(n^2)— For the difference and answer matrices.