Insert Interval
Problem
Given a set of non-overlapping & sorted intervals by start time, insert a new interval into the intervals (merge if necessary).
OR
You are given an array of non-overlapping intervals intervals where intervals[i] = [starti, endi] represent the start and the end of the ith interval and intervals is sorted in ascending order by starti. You are also given an interval newInterval = [start, end] that represents the start and end of another interval.
Insert newInterval into intervals such that intervals is still sorted in ascending order by starti and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return intervals after the insertion.
Examples
Example 1:
Input: intervals = [[1,3],[6,9]], newInterval = [2,5] y
Output: [[1,5],[6,9]]%% %%
Example 2:
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].
Solution
Video explanation
Here is the video explaining this method in detail. Please check it out:
<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/4apizj9b3Pw" frameborder="0" allowfullscreen></iframe></div>
Method 1 - Naive
The most straightforward way to solve this is to ignore the fact that the initial list is sorted. We can treat this problem as simply "merging a list of unsorted overlapping intervals". We have covered this problem here - [Merge Overlapping Intervals](merge-overlapping-intervals). The core idea is to add our new interval to the list and then use a standard merging algorithm. A standard merging algorithm requires the intervals to be sorted by their start times to work correctly.
Complexity
- ⏰ Time complexity:
O(n log n). Dominated by the sorting step. - 🧺 Space complexity:
O(n). To store themergedlist.
Method 1 - Greedy with 3 loops
If the list was not sorted, we could have appended the newInterval to the end of list. And then the problem was [Merge Overlapping Intervals](merge-overlapping-intervals).
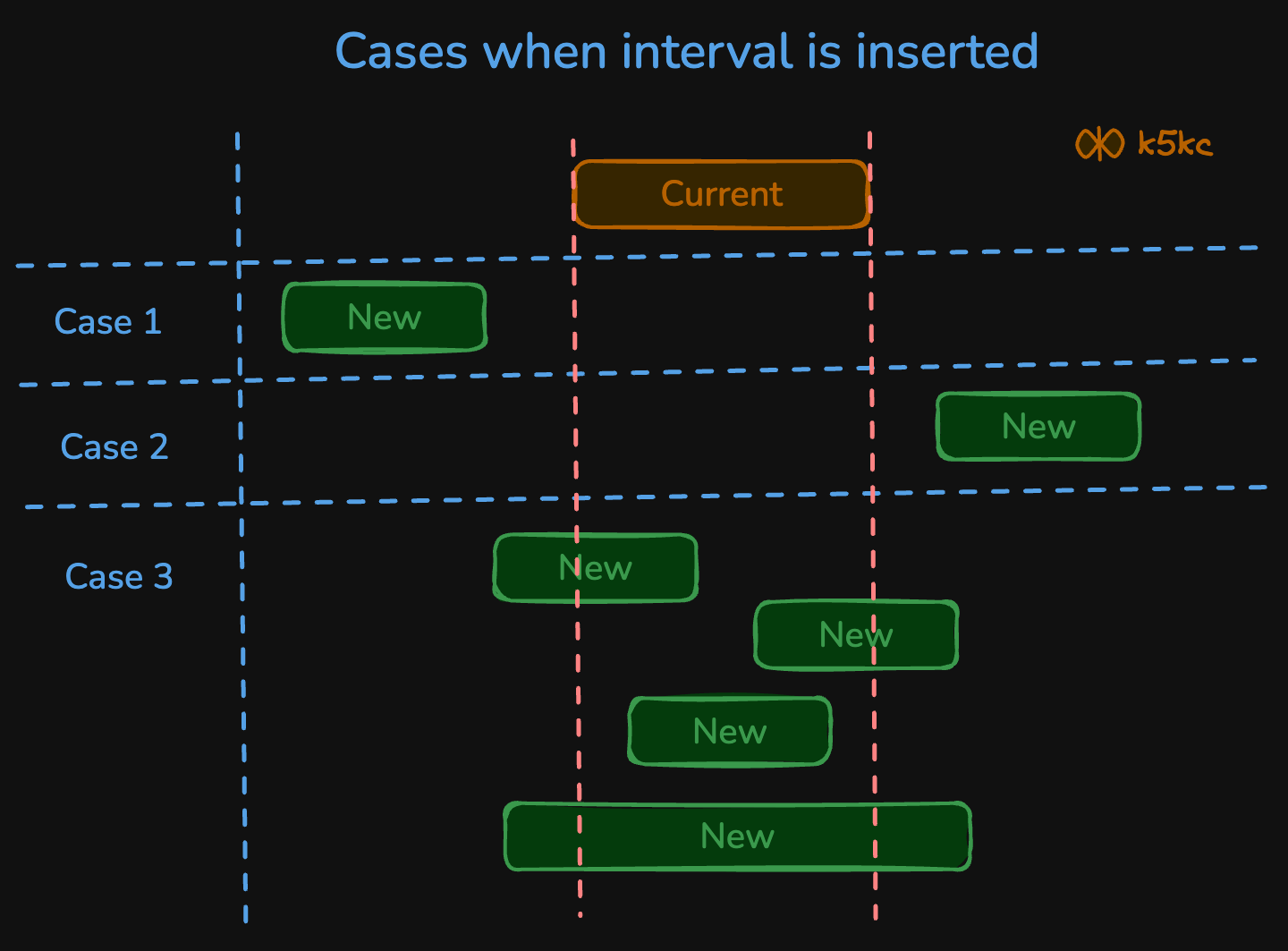
But, given that the intervals are sorted, our task simplifies to finding the correct index where the newInterval can be placed. By We can iterate through given intervals list, and we encounter three scenarios:
- Before New Interval (
newInterval.end <interval.start): If the end ofnewIntervalis before the start of the current interval, we insertnewIntervalinto the list at this position. - After New Interval (
newInterval.start > interval.end): If the start ofnewIntervalis after the end of the current interval, we skip these intervals and eventually insertnewIntervalafter the current interval. - Overlapping Intervals: When there is an overlap, we merge
newIntervalwith the current interval. The merged interval will have:c.start=min(newInterval.start, interval.start)andc.end=max(newInterval.end, interval.end)
Here is the visual view of how the 3 cases will look. Whenever there is intersection, created a new interval.
Code
Java
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> result = new ArrayList<>();
int i = 0;
int n = intervals.length;
// Case 1: Add all intervals that come before newInterval and don't overlap
while (i < n && intervals[i][1] < newInterval[0]) {
result.add(intervals[i]);
i++;
}
// Case 2: Merge newInterval with all overlapping intervals
while (i < n && intervals[i][0] <= newInterval[1]) {
newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
newInterval[1] = Math.max(newInterval[1], intervals[i][1]);
i++;
}
result.add(newInterval); // Add the merged newInterval
// Case 3: Add all intervals that come after newInterval and don't overlap
while (i < n) {
result.add(intervals[i]);
i++;
}
return result.toArray(new int[result.size()][]);
}
}
Python
class Solution:
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
result = []
i = 0
n = len(intervals)
# Case 1: Add all intervals that come before newInterval and don't overlap
while i < n and intervals[i][1] < newInterval[0]:
result.append(intervals[i])
i += 1
# Case 2: Merge newInterval with all overlapping intervals
while i < n and intervals[i][0] <= newInterval[1]:
newInterval[0] = min(newInterval[0], intervals[i][0])
newInterval[1] = max(newInterval[1], intervals[i][1])
i += 1
result.append(newInterval) # Add the merged newInterval
# Case 3: Add all intervals that come after newInterval and don't overlap
while i < n:
result.append(intervals[i])
i += 1
return result
Complexity
- ⏰ Time complexity:
O(n), as we iterate through the list only once. - 🧺 Space complexity:
O(n), to store the result list.
Method 3 - Greedy with 1 loop
This is similar to previous approach, just doing everything in one loop.
Code
Java
Interval Array
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> ans = new LinkedList<>();
for(int[] interval: intervals){
if(interval[1] < newInterval[0]){
ans.add(interval);
}else if(interval[0] > newInterval[1]){
ans.add(newInterval);
newInterval = interval;
}else if(interval[1] >= newInterval[0] || interval[0] <= newInterval[1]){
int start = Math.min(interval[0], newInterval[0]);
int end = Math.max(interval[1], newInterval[1]);
newInterval = new int[]{start, end};
}
}
ans.add(newInterval);
return ans.toArray(int[][]::new);
}
}
Interval Object
class Solution {
public List<Interval> insert(List<Interval> intervals, Interval newInterval) {
List<Interval> ans = new ArrayList<Interval> ();
for (Interval interval: intervals) {
if (interval.end<newInterval.start) {
ans.add(interval);
} else if (interval.start > newInterval.end) {
ans.add(newInterval);
newInterval = interval;
} else if (interval.end >= newInterval.start || interval.start<= newInterval.end) {
newInterval = new Interval(Math.min(interval.start, newInterval.start), Math.max(newInterval.end, interval.end));
}
}
ans.add(newInterval);
return ans;
}
}
Python
class Solution:
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
result = []
for interval in intervals:
# Case 1: current interval is after newInterval
# We need to add the newInterval and then update it to the current interval
if interval[1] < newInterval[0]:
result.append(newInterval)
newInterval = interval
# Case 2: current interval is before newInterval
elif interval[0] > newInterval[1]:
result.append(interval)
# Case 3: Overlap
else:
newInterval[0] = min(interval[0], newInterval[0])
newInterval[1] = max(interval[1], newInterval[1])
result.append(newInterval) # Add the final merged newInterval
return result
Rust
impl Solution {
pub fn insert(intervals: Vec<Vec<i32>>, new_interval: Vec<i32>) -> Vec<Vec<i32>> {
use std::cmp::{min, max};
let mut ans = vec![];
let mut new_interval = new_interval;
for interval in intervals {
if interval[1] < new_interval[0] {
ans.push(interval);
}else if interval[0] > new_interval[1] {
ans.push(new_interval);
new_interval = interval;
}else {
let start = min(interval[0], new_interval[0]);
let end = max(interval[1], new_interval[1]);
new_interval = vec![start, end];
}
}
ans.push(new_interval);
ans
}
}
Complexity
- ⏰ Time complexity:
O(n), as we iterate through the list only once. - 🧺 Space complexity:
O(n), to store the result list.