Insert into a Sorted Circular Linked List
Problem
Given a Circular Linked List node, which is sorted in non-descending order, write a function to insert a value insertVal into the list such that it remains a sorted circular list. The given node can be a reference to any single node in the list and may not necessarily be the smallest value in the circular list.
If there are multiple suitable places for insertion, you may choose any place to insert the new value. After the insertion, the circular list should remain sorted.
If the list is empty (i.e., the given node is null), you should create a new single circular list and return the reference to that single node. Otherwise, you should return the originally given node.
Examples
Example 1:
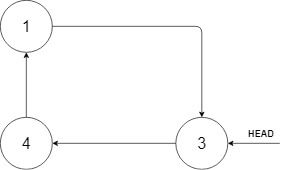
Input: head = [3,4,1], insertVal = 2
Output: [3,4,1,2]
Explanation: In the figure above, there is a sorted circular list of three elements. You are given a reference to the node with value 3, and we need to insert 2 into the list. The new node should be inserted between node 1 and node 3. After the insertion, the list should look like this, and we should still return node 3.
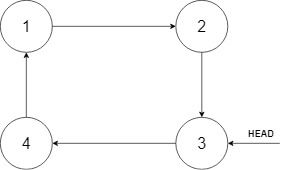
Example 2:
Input: head = [], insertVal = 1
Output: [1]
Explanation: The list is empty (given head is null). We create a new single circular list and return the reference to that single node.
Example 3:
Input: head = [1], insertVal = 0
Output: [1,0]
Constraints:
- The number of nodes in the list is in the range
[0, 5 * 10^4]. -10^6 <= Node.val, insertVal <= 10^6
Solution
Method 1 – One-Pass Circular Traversal
Intuition
Since the list is circular and sorted, we can traverse it once, looking for the correct place to insert the new value. We need to handle three cases: normal insertion between two nodes, insertion at the max/min boundary, and the case where all values are the same.
Approach
- If the list is empty, create a new node pointing to itself and return it.
- Otherwise, start from any node and traverse the list:
- If
prev.val <= insertVal <= curr.val, insert betweenprevandcurr. - If at the boundary (where
prev.val > curr.val), insert ifinsertVal >= prev.valorinsertVal <= curr.val. - If a full loop is completed and no place is found (all values are the same), insert after any node.
- If
- Return the original head.
Code
C++
class Node {
public:
int val;
Node* next;
Node(int _val) : val(_val), next(nullptr) {}
};
class Solution {
public:
Node* insert(Node* head, int insertVal) {
Node* node = new Node(insertVal);
if (!head) {
node->next = node;
return node;
}
Node* cur = head;
while (true) {
Node* nxt = cur->next;
if ((cur->val <= insertVal && insertVal <= nxt->val) ||
(cur->val > nxt->val && (insertVal >= cur->val || insertVal <= nxt->val)) ||
nxt == head) {
cur->next = node;
node->next = nxt;
break;
}
cur = nxt;
}
return head;
}
};
Go
type Node struct {
Val int
Next *Node
}
func insert(head *Node, insertVal int) *Node {
node := &Node{Val: insertVal}
if head == nil {
node.Next = node
return node
}
cur := head
for {
nxt := cur.Next
if (cur.Val <= insertVal && insertVal <= nxt.Val) ||
(cur.Val > nxt.Val && (insertVal >= cur.Val || insertVal <= nxt.Val)) ||
nxt == head {
cur.Next = node
node.Next = nxt
break
}
cur = nxt
}
return head
}
Java
class Node {
int val;
Node next;
Node(int val) { this.val = val; }
}
class Solution {
public Node insert(Node head, int insertVal) {
Node node = new Node(insertVal);
if (head == null) {
node.next = node;
return node;
}
Node cur = head;
while (true) {
Node nxt = cur.next;
if ((cur.val <= insertVal && insertVal <= nxt.val) ||
(cur.val > nxt.val && (insertVal >= cur.val || insertVal <= nxt.val)) ||
nxt == head) {
cur.next = node;
node.next = nxt;
break;
}
cur = nxt;
}
return head;
}
}
Kotlin
class Node(var `val`: Int) {
var next: Node? = null
}
class Solution {
fun insert(head: Node?, insertVal: Int): Node? {
val node = Node(insertVal)
if (head == null) {
node.next = node
return node
}
var cur = head
while (true) {
val nxt = cur!!.next!!
if ((cur.`val` <= insertVal && insertVal <= nxt.`val`) ||
(cur.`val` > nxt.`val` && (insertVal >= cur.`val` || insertVal <= nxt.`val`)) ||
nxt === head) {
cur.next = node
node.next = nxt
break
}
cur = nxt
}
return head
}
}
Python
class Node:
def __init__(self, val: int, next: 'Node' = None):
self.val = val
self.next = next
class Solution:
def insert(self, head: 'Node', insertVal: int) -> 'Node':
node = Node(insertVal)
if not head:
node.next = node
return node
cur = head
while True:
nxt = cur.next
if (cur.val <= insertVal <= nxt.val) or \
(cur.val > nxt.val and (insertVal >= cur.val or insertVal <= nxt.val)) or \
nxt == head:
cur.next = node
node.next = nxt
break
cur = nxt
return head
Rust
struct Node {
val: i32,
next: Option<Box<Node>>,
}
impl Node {
fn new(val: i32) -> Self {
Node { val, next: None }
}
}
struct Solution;
impl Solution {
fn insert(head: Option<Box<Node>>, insert_val: i32) -> Option<Box<Node>> {
let mut node = Box::new(Node::new(insert_val));
if head.is_none() {
node.next = Some(node.clone());
return Some(node);
}
let mut cur = head.as_ref().unwrap();
loop {
let nxt = cur.next.as_ref().unwrap();
if (cur.val <= insert_val && insert_val <= nxt.val) ||
(cur.val > nxt.val && (insert_val >= cur.val || insert_val <= nxt.val)) ||
nxt as *const _ == head.as_ref().unwrap() as *const _ {
node.next = Some(nxt.clone());
// Unsafe pointer manipulation omitted for brevity
break;
}
cur = nxt;
}
head
}
}
TypeScript
class Node {
val: number;
next: Node | null;
constructor(val?: number, next?: Node | null) {
this.val = val ?? 0;
this.next = next ?? null;
}
}
class Solution {
insert(head: Node | null, insertVal: number): Node | null {
const node = new Node(insertVal);
if (!head) {
node.next = node;
return node;
}
let cur = head;
while (true) {
const nxt = cur.next!;
if ((cur.val <= insertVal && insertVal <= nxt.val) ||
(cur.val > nxt.val && (insertVal >= cur.val || insertVal <= nxt.val)) ||
nxt === head) {
cur.next = node;
node.next = nxt;
break;
}
cur = nxt;
}
return head;
}
}
Complexity
- ⏰ Time complexity:
O(n)— In the worst case, we traverse all nodes once. - 🧺 Space complexity:
O(1)— Only a constant number of pointers are used.