Insufficient Nodes in Root to Leaf Paths
MediumUpdated: Aug 2, 2025
Practice on:
Problem
Given the root of a binary tree and an integer limit, delete all
insufficient nodes in the tree simultaneously, and return the root of the resulting binary tree.
A node is insufficient if every root to leaf path intersecting this node has a sum strictly less than limit.
A leaf is a node with no children.
Examples
Example 1
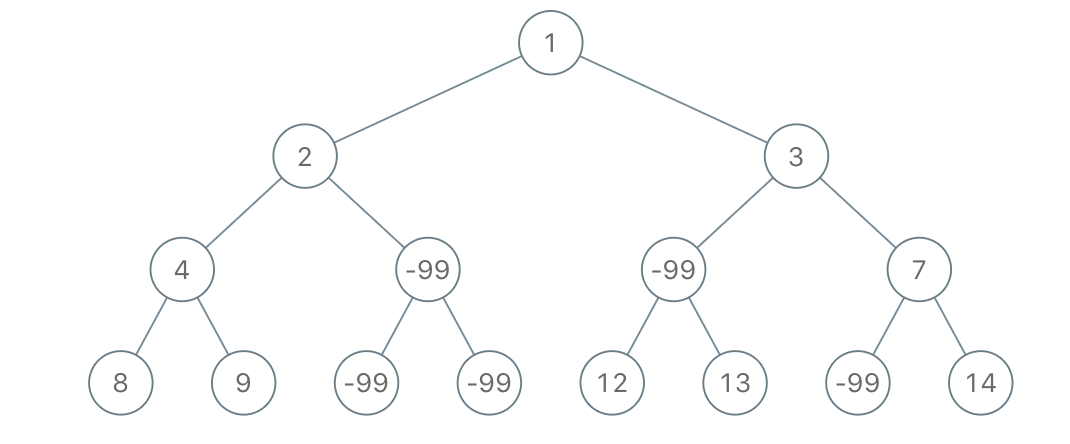
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
Output: [1,2,3,4,null,null,7,8,9,null,14]
Example 2
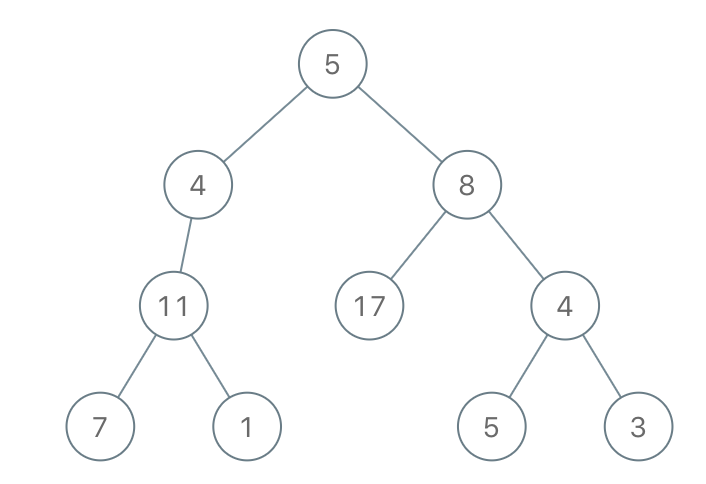
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
Output: [5,4,8,11,null,17,4,7,null,null,null,5]
Example 3
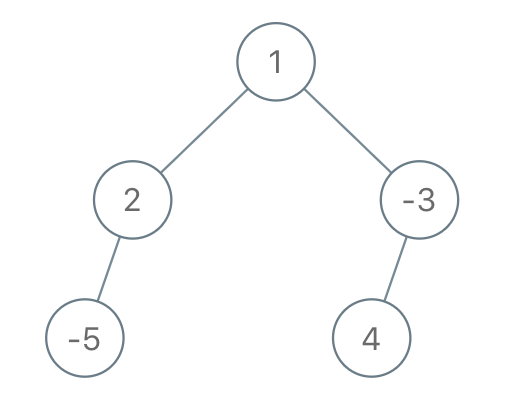
Input: root = [1,2,-3,-5,null,4,null], limit = -1
Output: [1,null,-3,4]
Constraints
- The number of nodes in the tree is in the range
[1, 5000]. -10^5 <= Node.val <= 10^5-10^9 <= limit <= 10^9
Solution
Method 1 – Postorder DFS Pruning
Intuition
We want to remove nodes where every root-to-leaf path through that node has a sum less than the limit. By using postorder DFS, we can check the sum for each subtree and prune insufficient nodes from the bottom up.
Approach
- Use a recursive DFS function that returns the pruned subtree.
- For each node:
- If it is a leaf, check if the path sum including this node is at least the limit. If not, return null.
- Recursively prune left and right children, passing the updated sum.
- If both children are pruned (null), and the node is not sufficient, prune this node as well.
- Return the pruned tree.
Code
C++
struct TreeNode {
int val;
TreeNode *left, *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
TreeNode* sufficientSubset(TreeNode* root, int limit) {
return dfs(root, 0, limit);
}
private:
TreeNode* dfs(TreeNode* node, int sum, int limit) {
if (!node) return nullptr;
sum += node->val;
if (!node->left && !node->right)
return sum >= limit ? node : nullptr;
node->left = dfs(node->left, sum, limit);
node->right = dfs(node->right, sum, limit);
if (!node->left && !node->right) return nullptr;
return node;
}
};
Go
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func sufficientSubset(root *TreeNode, limit int) *TreeNode {
var dfs func(*TreeNode, int) *TreeNode
dfs = func(node *TreeNode, sum int) *TreeNode {
if node == nil {
return nil
}
sum += node.Val
if node.Left == nil && node.Right == nil {
if sum >= limit {
return node
}
return nil
}
node.Left = dfs(node.Left, sum)
node.Right = dfs(node.Right, sum)
if node.Left == nil && node.Right == nil {
return nil
}
return node
}
return dfs(root, 0)
}
Java
class TreeNode {
int val;
TreeNode left, right;
TreeNode(int x) { val = x; }
}
class Solution {
public TreeNode sufficientSubset(TreeNode root, int limit) {
return dfs(root, 0, limit);
}
private TreeNode dfs(TreeNode node, int sum, int limit) {
if (node == null) return null;
sum += node.val;
if (node.left == null && node.right == null)
return sum >= limit ? node : null;
node.left = dfs(node.left, sum, limit);
node.right = dfs(node.right, sum, limit);
if (node.left == null && node.right == null) return null;
return node;
}
}
Kotlin
data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
fun sufficientSubset(root: TreeNode?, limit: Int): TreeNode? {
fun dfs(node: TreeNode?, sum: Int): TreeNode? {
if (node == null) return null
val s = sum + node.`val`
if (node.left == null && node.right == null)
return if (s >= limit) node else null
node.left = dfs(node.left, s)
node.right = dfs(node.right, s)
return if (node.left == null && node.right == null) null else node
}
return dfs(root, 0)
}
}
Python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def sufficientSubset(self, root: TreeNode, limit: int) -> TreeNode:
def dfs(node: TreeNode, s: int) -> TreeNode:
if not node:
return None
s += node.val
if not node.left and not node.right:
return node if s >= limit else None
node.left = dfs(node.left, s)
node.right = dfs(node.right, s)
if not node.left and not node.right:
return None
return node
return dfs(root, 0)
Rust
use std::rc::Rc;
use std::cell::RefCell;
#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
pub val: i32,
pub left: Option<Rc<RefCell<TreeNode>>>,
pub right: Option<Rc<RefCell<TreeNode>>>,
}
impl TreeNode {
#[inline]
pub fn new(val: i32) -> Self {
TreeNode { val, left: None, right: None }
}
}
pub struct Solution;
impl Solution {
pub fn sufficient_subset(root: Option<Rc<RefCell<TreeNode>>>, limit: i32) -> Option<Rc<RefCell<TreeNode>>> {
fn dfs(node: Option<Rc<RefCell<TreeNode>>>, sum: i32, limit: i32) -> Option<Rc<RefCell<TreeNode>>> {
if let Some(n) = node {
let mut n = n.borrow_mut();
let s = sum + n.val;
if n.left.is_none() && n.right.is_none() {
return if s >= limit { Some(Rc::new(RefCell::new(TreeNode::new(n.val)))) } else { None };
}
n.left = dfs(n.left.take(), s, limit);
n.right = dfs(n.right.take(), s, limit);
if n.left.is_none() && n.right.is_none() {
return None;
}
return Some(Rc::new(RefCell::new(TreeNode {
val: n.val,
left: n.left.clone(),
right: n.right.clone(),
})));
}
None
}
dfs(root, 0, limit)
}
}
TypeScript
class TreeNode {
val: number;
left: TreeNode | null;
right: TreeNode | null;
constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
this.val = val ?? 0;
this.left = left ?? null;
this.right = right ?? null;
}
}
class Solution {
sufficientSubset(root: TreeNode | null, limit: number): TreeNode | null {
function dfs(node: TreeNode | null, s: number): TreeNode | null {
if (!node) return null;
s += node.val;
if (!node.left && !node.right) return s >= limit ? node : null;
node.left = dfs(node.left, s);
node.right = dfs(node.right, s);
if (!node.left && !node.right) return null;
return node;
}
return dfs(root, 0);
}
}
Complexity
- ⏰ Time complexity:
O(n)— Each node is visited once. - 🧺 Space complexity:
O(h)— Call stack for recursion, where h is the height of the tree.