Is Array a Preorder of Some ‌Binary Tree

Problem

Given a 0-indexed integer 2D array nodes, your task is to determine if the given array represents the preorder traversal of some binary tree.

For each index i, nodes[i] = [id, parentId], where id is the id of the node at the index i and parentId is the id of its parent in the tree (if the node has no parent, then parentId == -1).

Return true if the given array represents the preorder traversal of some tree, and false otherwise.

Note: the preorder traversal of a tree is a recursive way to traverse a tree in which we first visit the current node, then we do the preorder traversal for the left child, and finally, we do it for the right child.

Examples

Example 1:

1
2
3
4
5


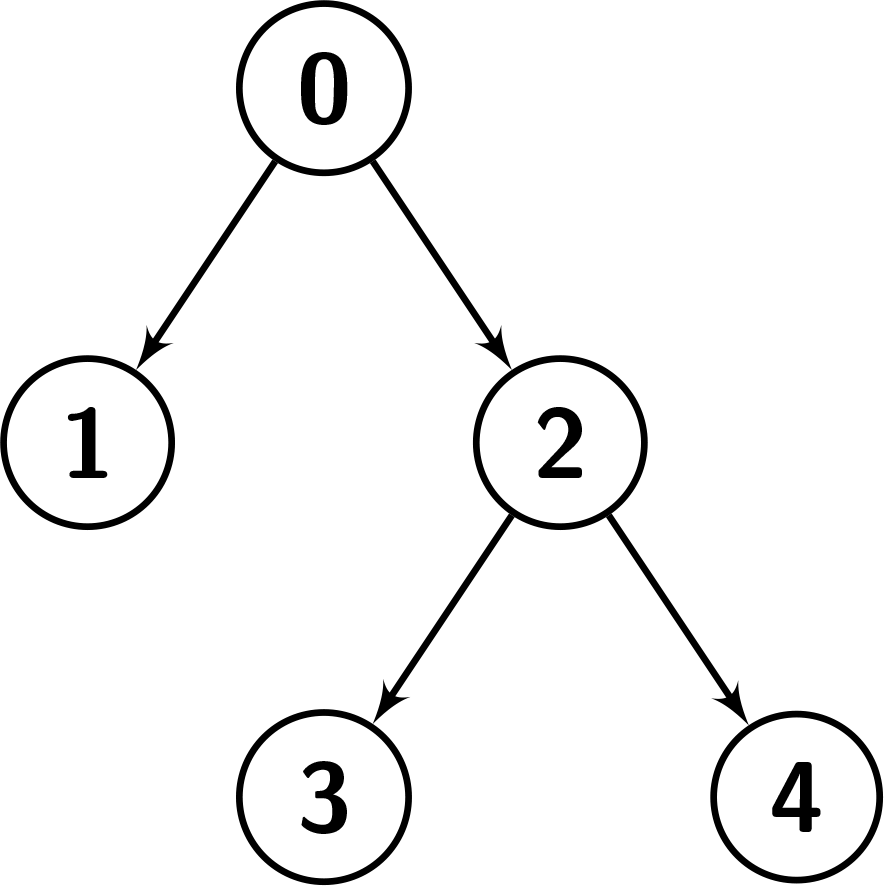
Input: nodes = [[0,-1],[1,0],[2,0],[3,2],[4,2]]
Output: true
Explanation: The given nodes make the tree in the picture below.
We can show that this is the preorder traversal of the tree, first we visit node 0, then we do the preorder traversal of the right child which is [1], then we do the preorder traversal of the left child which is [2,3,4].
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2700-2799/2764.Is%20Array%20a%20Preorder%20of%20Some%20%E2%80%8CBinary%20Tree/images/1.png)

Example 2:

1
2
3
4
5


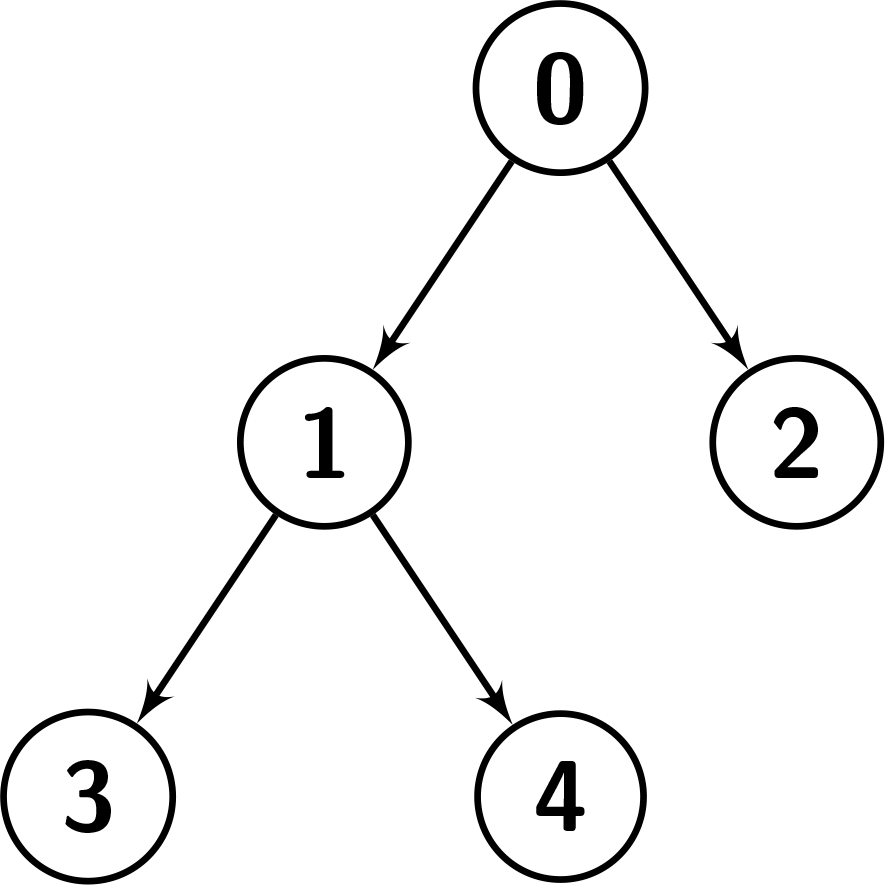
Input: nodes = [[0,-1],[1,0],[2,0],[3,1],[4,1]]
Output: false
Explanation: The given nodes make the tree in the picture below.
For the preorder traversal, first we visit node 0, then we do the preorder traversal of the right child which is [1,3,4], but we can see that in the given order, 2 comes between 1 and 3, so, it's not the preorder traversal of the tree.
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2700-2799/2764.Is%20Array%20a%20Preorder%20of%20Some%20%E2%80%8CBinary%20Tree/images/2.png)

Constraints:

1 <= nodes.length <= 10^5
nodes[i].length == 2
0 <= nodes[i][0] <= 10^5
-1 <= nodes[i][1] <= 10^5
The input is generated such that nodes make a binary tree.

Solution

Method 1 – Stack Simulation (Parent-Child Validation)

Intuition

To check if the given array is a valid preorder traversal of a binary tree, we simulate the traversal using a stack. We ensure that each node’s parent appears before it and that the parent-child relationships are consistent with preorder traversal.

Approach

Create a map from node id to its index in the array for quick lookup.
Initialize an empty stack.
Iterate through the nodes:
- If the node is a root (parentId == -1), push it to the stack.
- Otherwise, check if the parent is at the top of the stack. If not, pop from the stack until the parent is found or the stack is empty.
- If the parent is not found, return false.
- Push the current node to the stack.
If all nodes are processed without conflict, return true.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    bool validateBinaryTreeNodes(vector<vector<int>>& nodes) {
        int n = nodes.size();
        unordered_map<int, int> idx;
        for (int i = 0; i < n; ++i) idx[nodes[i][0]] = i;
        stack<int> st;
        for (int i = 0; i < n; ++i) {
            int id = nodes[i][0], par = nodes[i][1];
            if (par == -1) st.push(id);
            else {
                while (!st.empty() && st.top() != par) st.pop();
                if (st.empty()) return false;
                st.push(id);
            }
        }
        return true;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


func validateBinaryTreeNodes(nodes [][]int) bool {
    idx := map[int]int{}
    for i, v := range nodes {
        idx[v[0]] = i
    }
    st := []int{}
    for _, v := range nodes {
        id, par := v[0], v[1]
        if par == -1 {
            st = append(st, id)
        } else {
            for len(st) > 0 && st[len(st)-1] != par {
                st = st[:len(st)-1]
            }
            if len(st) == 0 {
                return false
            }
            st = append(st, id)
        }
    }
    return true
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
    public boolean validateBinaryTreeNodes(int[][] nodes) {
        int n = nodes.length;
        Map<Integer, Integer> idx = new HashMap<>();
        for (int i = 0; i < n; ++i) idx.put(nodes[i][0], i);
        Deque<Integer> st = new ArrayDeque<>();
        for (int i = 0; i < n; ++i) {
            int id = nodes[i][0], par = nodes[i][1];
            if (par == -1) st.push(id);
            else {
                while (!st.isEmpty() && st.peek() != par) st.pop();
                if (st.isEmpty()) return false;
                st.push(id);
            }
        }
        return true;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution {
    fun validateBinaryTreeNodes(nodes: Array<IntArray>): Boolean {
        val idx = mutableMapOf<Int, Int>()
        for (i in nodes.indices) idx[nodes[i][0]] = i
        val st = ArrayDeque<Int>()
        for (v in nodes) {
            val id = v[0]; val par = v[1]
            if (par == -1) st.addLast(id)
            else {
                while (st.isNotEmpty() && st.last() != par) st.removeLast()
                if (st.isEmpty()) return false
                st.addLast(id)
            }
        }
        return true
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def validate_binary_tree_nodes(nodes: list[list[int]]) -> bool:
    idx = {id: i for i, (id, _) in enumerate(nodes)}
    st = []
    for id, par in nodes:
        if par == -1:
            st.append(id)
        else:
            while st and st[-1] != par:
                st.pop()
            if not st:
                return False
            st.append(id)
    return True

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


use std::collections::HashMap;
fn validate_binary_tree_nodes(nodes: Vec<Vec<i32>>) -> bool {
    let mut idx = HashMap::new();
    for (i, v) in nodes.iter().enumerate() {
        idx.insert(v[0], i);
    }
    let mut st = vec![];
    for v in nodes {
        let id = v[0]; let par = v[1];
        if par == -1 {
            st.push(id);
        } else {
            while let Some(&top) = st.last() {
                if top == par { break; }
                st.pop();
            }
            if st.is_empty() { return false; }
            st.push(id);
        }
    }
    true
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


function validateBinaryTreeNodes(nodes: number[][]): boolean {
  const idx: Record<number, number> = {};
  for (let i = 0; i < nodes.length; ++i) idx[nodes[i][0]] = i;
  const st: number[] = [];
  for (const [id, par] of nodes) {
    if (par === -1) st.push(id);
    else {
      while (st.length && st[st.length-1] !== par) st.pop();
      if (!st.length) return false;
      st.push(id);
    }
  }
  return true;
}

Complexity

⏰ Time complexity: O(n) — Each node is pushed and popped at most once.
🧺 Space complexity: O(n) — For the stack and index map.

Problem#

Examples#

Solution#

Method 1 – Stack Simulation (Parent-Child Validation)#

Intuition#

Approach#

Code#

Complexity#