Jump Game 5

Problem

Given an array of integers arr and an integer d. In one step you can jump from index i to index:

i + x where: i + x < arr.length and 0 < x <= d.
i - x where: i - x >= 0 and 0 < x <= d.

In addition, you can only jump from index i to index j if arr[i] > arr[j] and arr[i] > arr[k] for all indices k between i and j (More formally min(i, j) < k < max(i, j)).

You can choose any index of the array and start jumping. Return the maximum number of indices you can visit.

Notice that you can not jump outside of the array at any time.

Examples

Example 1:

1
2
3
4
5


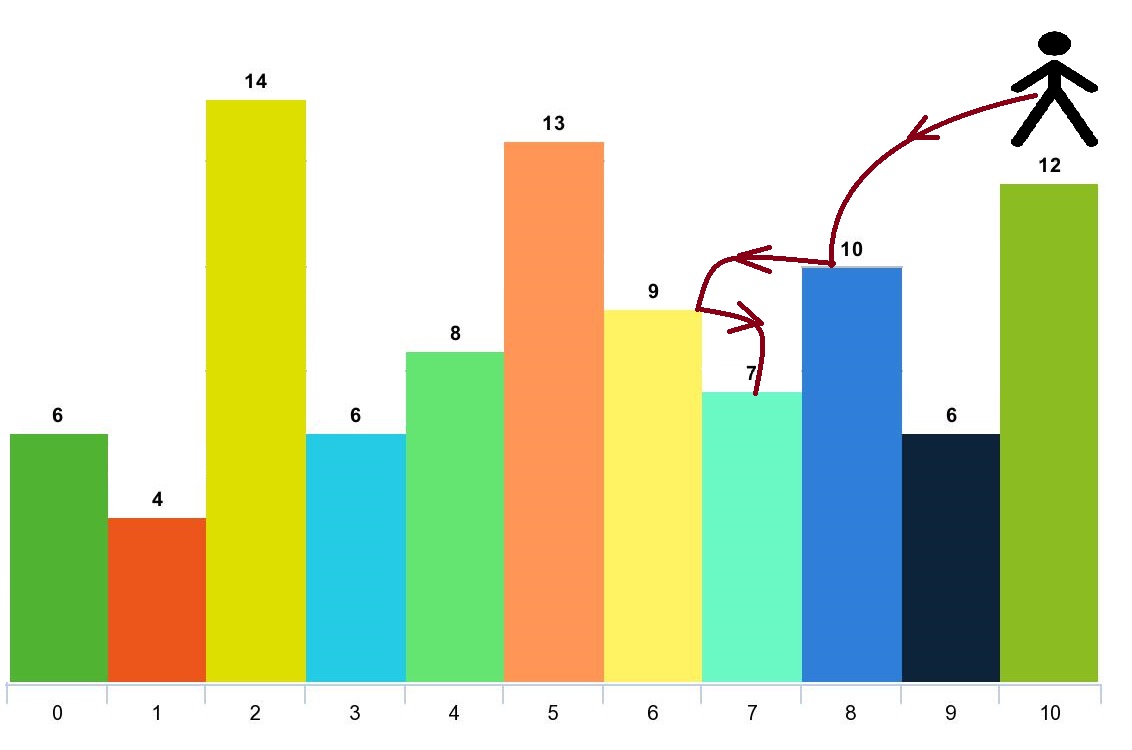
Input: arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
Output: 4
Explanation: You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.

Example 2:

1
2
3


Input: arr = [3,3,3,3,3], d = 3
Output: 1
Explanation: You can start at any index. You always cannot jump to any index.

Example 3:

1
2
3


Input: arr = [7,6,5,4,3,2,1], d = 1
Output: 7
Explanation: Start at index 0. You can visit all the indicies. 

Constraints:

1 <= arr.length <= 1000
1 <= arr[i] <= 10^5
1 <= d <= arr.length

Solution

Method 1 – Dynamic Programming with Memoization

Intuition

The problem asks for the maximum number of indices you can visit by jumping left or right up to d steps, but only to strictly lower values and without “jumping over” higher or equal values. The key insight is that from each index, the best you can do is the maximum of all possible valid jumps from that index, plus one (for the current index). Since jumps can overlap, we use memoization to avoid recomputation.

Approach

Define a recursive function dfs(i) that returns the maximum number of indices you can visit starting from index i.
Use a memoization array to store results for each index to avoid redundant calculations.
For each index, try all jumps to the left and right within distance d:

For each direction, stop if you hit an index with a value not less than the current.
For each valid jump, recursively compute the answer and keep track of the maximum.

The answer is the maximum value of dfs(i) for all indices i.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class Solution {
public:
   int maxJumps(vector<int>& arr, int d) {
      int n = arr.size();
      vector<int> memo(n, 0);
      function<int(int)> dfs = [&](int i) {
        if (memo[i]) return memo[i];
        int ans = 1;
        for (int dir = -1; dir <= 1; dir += 2) {
           for (int j = 1; j <= d; ++j) {
              int ni = i + dir * j;
              if (ni < 0 || ni >= n || arr[ni] >= arr[i]) break;
              ans = max(ans, 1 + dfs(ni));
           }
        }
        return memo[i] = ans;
      };
      int res = 0;
      for (int i = 0; i < n; ++i) res = max(res, dfs(i));
      return res;
   }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


func maxJumps(arr []int, d int) int {
   n := len(arr)
   memo := make([]int, n)
   var dfs func(i int) int
   dfs = func(i int) int {
      if memo[i] > 0 {
        return memo[i]
      }
      ans := 1
      for _, dir := range []int{-1, 1} {
        for j := 1; j <= d; j++ {
           ni := i + dir*j
           if ni < 0 || ni >= n || arr[ni] >= arr[i] {
              break
           }
           if v := 1 + dfs(ni); v > ans {
              ans = v
           }
        }
      }
      memo[i] = ans
      return ans
   }
   res := 0
   for i := 0; i < n; i++ {
      if v := dfs(i); v > res {
        res = v
      }
   }
   return res
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution {
   public int maxJumps(int[] arr, int d) {
      int n = arr.length;
      int[] memo = new int[n];
      return java.util.stream.IntStream.range(0, n)
        .map(i -> dfs(arr, d, i, memo))
        .max().getAsInt();
   }
   private int dfs(int[] arr, int d, int i, int[] memo) {
      if (memo[i] != 0) return memo[i];
      int ans = 1, n = arr.length;
      for (int dir = -1; dir <= 1; dir += 2) {
        for (int j = 1; j <= d; ++j) {
           int ni = i + dir * j;
           if (ni < 0 || ni >= n || arr[ni] >= arr[i]) break;
           ans = Math.max(ans, 1 + dfs(arr, d, ni, memo));
        }
      }
      return memo[i] = ans;
   }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
   fun maxJumps(arr: IntArray, d: Int): Int {
      val n = arr.size
      val memo = IntArray(n)
      fun dfs(i: Int): Int {
        if (memo[i] != 0) return memo[i]
        var ans = 1
        for (dir in listOf(-1, 1)) {
           for (j in 1..d) {
              val ni = i + dir * j
              if (ni !in 0 until n || arr[ni] >= arr[i]) break
              ans = maxOf(ans, 1 + dfs(ni))
           }
        }
        memo[i] = ans
        return ans
      }
      return (0 until n).maxOf { dfs(it) }
   }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution:
   def maxJumps(self, arr: list[int], d: int) -> int:
      n: int = len(arr)
      memo: list[int] = [0] * n

      def dfs(i: int) -> int:
        if memo[i]:
           return memo[i]
        ans: int = 1
        for dir in (-1, 1):
           for j in range(1, d + 1):
              ni: int = i + dir * j
              if ni < 0 or ni >= n or arr[ni] >= arr[i]:
                break
              ans = max(ans, 1 + dfs(ni))
        memo[i] = ans
        return ans

      return max(dfs(i) for i in range(n))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


impl Solution {
   pub fn max_jumps(arr: Vec<i32>, d: i32) -> i32 {
      fn dfs(i: usize, arr: &Vec<i32>, d: i32, memo: &mut Vec<i32>) -> i32 {
        if memo[i] != 0 { return memo[i]; }
        let n = arr.len();
        let mut ans = 1;
        for &dir in &[-1, 1] {
           for j in 1..=d {
              let ni = i as i32 + dir * j;
              if ni < 0 || ni >= n as i32 || arr[ni as usize] >= arr[i] { break; }
              ans = ans.max(1 + dfs(ni as usize, arr, d, memo));
           }
        }
        memo[i] = ans;
        ans
      }
      let n = arr.len();
      let mut memo = vec![0; n];
      (0..n).map(|i| dfs(i, &arr, d, &mut memo)).max().unwrap()
   }
}

Complexity

⏰ Time complexity: O(n * d) where n is the length of arr (each index is visited once, and for each, up to d jumps are checked in both directions).
🧺 Space complexity: O(n) for the memoization array and recursion stack.

Problem#

Examples#

Similar Problems#

Solution#

Method 1 – Dynamic Programming with Memoization#

Intuition#

Approach#

Code#

Complexity#