K Highest Ranked Items Within a Price Range
Problem
You are given a 0-indexed 2D integer array grid of size m x n that represents a map of the items in a shop. The integers in the grid represent the following:
0represents a wall that you cannot pass through.1represents an empty cell that you can freely move to and from.- All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells.
It takes 1 step to travel between adjacent grid cells.
You are also given integer arrays pricing and start where pricing = [low, high] and start = [row, col] indicates that you start at the position
(row, col) and are interested only in items with a price in the range of
[low, high] (inclusive). You are further given an integer k.
You are interested in the positions of the k highest-ranked items whose prices are within the given price range. The rank is determined by the first of these criteria that is different:
- Distance, defined as the length of the shortest path from the
start(shorter distance has a higher rank). - Price (lower price has a higher rank, but it must be in the price range).
- The row number (smaller row number has a higher rank).
- The column number (smaller column number has a higher rank).
Return thek highest-ranked items within the price rangesorted by their rank (highest to lowest). If there are fewer than k reachable items within the price range, return all of them.
Examples
Example 1
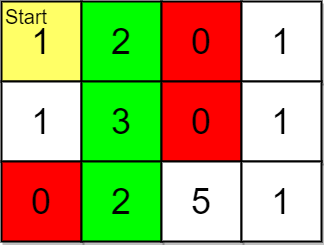
Input: grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
Output: [[0,1],[1,1],[2,1]]
Explanation: You start at (0,0).
With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2).
The ranks of these items are:
- (0,1) with distance 1
- (1,1) with distance 2
- (2,1) with distance 3
- (2,2) with distance 4
Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1).
Example 2
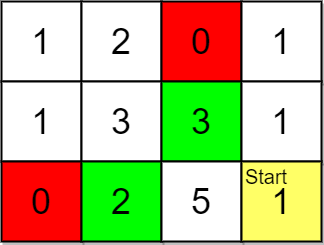
Input: grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
Output: [[2,1],[1,2]]
Explanation: You start at (2,3).
With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1).
The ranks of these items are:
- (2,1) with distance 2, price 2
- (1,2) with distance 2, price 3
- (1,1) with distance 3
- (0,1) with distance 4
Thus, the 2 highest ranked items in the price range are (2,1) and (1,2).
Example 3
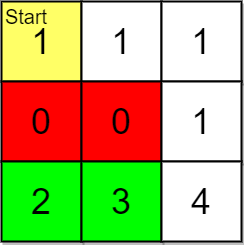
Input: grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
Output: [[2,1],[2,0]]
Explanation: You start at (0,0).
With a price range of [2,3], we can take items from (2,0) and (2,1).
The ranks of these items are:
- (2,1) with distance 5
- (2,0) with distance 6
Thus, the 2 highest ranked items in the price range are (2,1) and (2,0).
Note that k = 3 but there are only 2 reachable items within the price range.
Constraints
m == grid.lengthn == grid[i].length1 <= m, n <= 10^51 <= m * n <= 10^50 <= grid[i][j] <= 10^5pricing.length == 22 <= low <= high <= 10^5start.length == 20 <= row <= m - 10 <= col <= n - 1grid[row][col] > 01 <= k <= m * n
Solution
Method 1 – Breadth-First Search with Sorting
Intuition
We want to find the k highest-ranked items within a price range, where rank is determined by shortest distance from the start, then by lowest price, then by row, then by column. BFS is ideal for finding shortest paths in a grid, and we can collect all valid items and sort them by the required criteria.
Approach
- Use BFS from the start cell to explore all reachable cells, tracking distance.
- For each cell, if its value is within the price range, record its (distance, price, row, col).
- After BFS, sort the collected items by (distance, price, row, col).
- Return the first k items' positions.
Code
C++
class Solution {
public:
vector<vector<int>> highestRankedKItems(vector<vector<int>>& grid, vector<int>& pricing, vector<int>& start, int k) {
int m = grid.size(), n = grid[0].size();
vector<vector<bool>> vis(m, vector<bool>(n, false));
queue<pair<int, int>> q;
vector<tuple<int, int, int, int>> items;
int dirs[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
q.push({start[0], start[1]});
vis[start[0]][start[1]] = true;
int dist = 0;
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; ++i) {
auto [r, c] = q.front(); q.pop();
int val = grid[r][c];
if (val >= pricing[0] && val <= pricing[1])
items.emplace_back(dist, val, r, c);
for (auto& d : dirs) {
int nr = r + d[0], nc = c + d[1];
if (nr >= 0 && nr < m && nc >= 0 && nc < n && !vis[nr][nc] && grid[nr][nc] != 0) {
vis[nr][nc] = true;
q.push({nr, nc});
}
}
}
++dist;
}
sort(items.begin(), items.end());
vector<vector<int>> ans;
for (int i = 0; i < items.size() && ans.size() < k; ++i) {
auto [d, v, r, c] = items[i];
ans.push_back({r, c});
}
return ans;
}
};
Go
type tuple struct{d, v, r, c int}
func highestRankedKItems(grid [][]int, pricing []int, start []int, k int) [][]int {
m, n := len(grid), len(grid[0])
vis := make([][]bool, m)
for i := range vis { vis[i] = make([]bool, n) }
dirs := [][2]int{{0,1},{1,0},{0,-1},{-1,0}}
q := [][2]int{{start[0], start[1]}}
vis[start[0]][start[1]] = true
items := []tuple{}
dist := 0
for len(q) > 0 {
sz := len(q)
for i := 0; i < sz; i++ {
r, c := q[0][0], q[0][1]
q = q[1:]
v := grid[r][c]
if v >= pricing[0] && v <= pricing[1] {
items = append(items, tuple{dist, v, r, c})
}
for _, d := range dirs {
nr, nc := r+d[0], c+d[1]
if nr>=0 && nr<m && nc>=0 && nc<n && !vis[nr][nc] && grid[nr][nc]!=0 {
vis[nr][nc] = true
q = append(q, [2]int{nr, nc})
}
}
}
dist++
}
sort.Slice(items, func(i, j int) bool {
a, b := items[i], items[j]
if a.d != b.d { return a.d < b.d }
if a.v != b.v { return a.v < b.v }
if a.r != b.r { return a.r < b.r }
return a.c < b.c
})
ans := [][]int{}
for i := 0; i < len(items) && len(ans) < k; i++ {
ans = append(ans, []int{items[i].r, items[i].c})
}
return ans
}
Java
class Solution {
public List<List<Integer>> highestRankedKItems(int[][] grid, int[] pricing, int[] start, int k) {
int m = grid.length, n = grid[0].length;
boolean[][] vis = new boolean[m][n];
Queue<int[]> q = new LinkedList<>();
List<int[]> items = new ArrayList<>();
int[][] dirs = {{0,1},{1,0},{0,-1},{-1,0}};
q.offer(new int[]{start[0], start[1]});
vis[start[0]][start[1]] = true;
int dist = 0;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; ++i) {
int[] cur = q.poll();
int r = cur[0], c = cur[1];
int v = grid[r][c];
if (v >= pricing[0] && v <= pricing[1])
items.add(new int[]{dist, v, r, c});
for (int[] d : dirs) {
int nr = r + d[0], nc = c + d[1];
if (nr >= 0 && nr < m && nc >= 0 && nc < n && !vis[nr][nc] && grid[nr][nc] != 0) {
vis[nr][nc] = true;
q.offer(new int[]{nr, nc});
}
}
}
++dist;
}
items.sort((a, b) -> {
if (a[0] != b[0]) return a[0] - b[0];
if (a[1] != b[1]) return a[1] - b[1];
if (a[2] != b[2]) return a[2] - b[2];
return a[3] - b[3];
});
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < items.size() && ans.size() < k; ++i) {
ans.add(Arrays.asList(items.get(i)[2], items.get(i)[3]));
}
return ans;
}
}
Kotlin
class Solution {
fun highestRankedKItems(grid: Array<IntArray>, pricing: IntArray, start: IntArray, k: Int): List<List<Int>> {
val m = grid.size
val n = grid[0].size
val vis = Array(m) { BooleanArray(n) }
val dirs = arrayOf(intArrayOf(0,1), intArrayOf(1,0), intArrayOf(0,-1), intArrayOf(-1,0))
val q = ArrayDeque<Pair<Int, Int>>()
val items = mutableListOf<Quadruple>()
q.add(Pair(start[0], start[1]))
vis[start[0]][start[1]] = true
var dist = 0
data class Quadruple(val d: Int, val v: Int, val r: Int, val c: Int)
while (q.isNotEmpty()) {
repeat(q.size) {
val (r, c) = q.removeFirst()
val v = grid[r][c]
if (v in pricing[0]..pricing[1]) items.add(Quadruple(dist, v, r, c))
for (d in dirs) {
val nr = r + d[0]
val nc = c + d[1]
if (nr in 0 until m && nc in 0 until n && !vis[nr][nc] && grid[nr][nc] != 0) {
vis[nr][nc] = true
q.add(Pair(nr, nc))
}
}
}
dist++
}
items.sortWith(compareBy({it.d}, {it.v}, {it.r}, {it.c}))
return items.take(k).map { listOf(it.r, it.c) }
}
}
Python
class Solution:
def highestRankedKItems(self, grid: list[list[int]], pricing: list[int], start: list[int], k: int) -> list[list[int]]:
m, n = len(grid), len(grid[0])
vis = [[False]*n for _ in range(m)]
q = [(start[0], start[1])]
vis[start[0]][start[1]] = True
items: list[tuple[int,int,int,int]] = []
dist = 0
dirs = [(0,1),(1,0),(0,-1),(-1,0)]
while q:
nq = []
for r, c in q:
v = grid[r][c]
if pricing[0] <= v <= pricing[1]:
items.append((dist, v, r, c))
for dr, dc in dirs:
nr, nc = r+dr, c+dc
if 0<=nr<m and 0<=nc<n and not vis[nr][nc] and grid[nr][nc]!=0:
vis[nr][nc] = True
nq.append((nr, nc))
q = nq
dist += 1
items.sort()
ans = []
for d, v, r, c in items:
if len(ans) == k: break
ans.append([r, c])
return ans
Rust
impl Solution {
pub fn highest_ranked_k_items(grid: Vec<Vec<i32>>, pricing: Vec<i32>, start: Vec<i32>, k: i32) -> Vec<Vec<i32>> {
use std::collections::{VecDeque, HashSet};
let m = grid.len();
let n = grid[0].len();
let mut vis = vec![vec![false; n]; m];
let mut q = VecDeque::new();
let mut items = vec![];
let dirs = [(0,1),(1,0),(0,-1),(-1,0)];
q.push_back((start[0] as usize, start[1] as usize));
vis[start[0] as usize][start[1] as usize] = true;
let mut dist = 0;
while !q.is_empty() {
for _ in 0..q.len() {
let (r, c) = q.pop_front().unwrap();
let v = grid[r][c];
if v >= pricing[0] && v <= pricing[1] {
items.push((dist, v, r, c));
}
for (dr, dc) in dirs.iter() {
let nr = r as i32 + dr;
let nc = c as i32 + dc;
if nr>=0 && nr<m as i32 && nc>=0 && nc<n as i32 {
let (nr, nc) = (nr as usize, nc as usize);
if !vis[nr][nc] && grid[nr][nc]!=0 {
vis[nr][nc] = true;
q.push_back((nr, nc));
}
}
}
}
dist += 1;
}
items.sort();
let mut ans = vec![];
for (d, v, r, c) in items {
if ans.len() == k as usize { break; }
ans.push(vec![r as i32, c as i32]);
}
ans
}
}
TypeScript
class Solution {
highestRankedKItems(grid: number[][], pricing: number[], start: number[], k: number): number[][] {
const m = grid.length, n = grid[0].length;
const vis = Array.from({length: m}, () => Array(n).fill(false));
const q: [number, number][] = [[start[0], start[1]]];
vis[start[0]][start[1]] = true;
let dist = 0;
const items: [number, number, number, number][] = [];
const dirs = [[0,1],[1,0],[0,-1],[-1,0]];
while (q.length) {
const nq: [number, number][] = [];
for (const [r, c] of q) {
const v = grid[r][c];
if (v >= pricing[0] && v <= pricing[1]) items.push([dist, v, r, c]);
for (const [dr, dc] of dirs) {
const nr = r+dr, nc = c+dc;
if (nr>=0 && nr<m && nc>=0 && nc<n && !vis[nr][nc] && grid[nr][nc]!=0) {
vis[nr][nc] = true;
nq.push([nr, nc]);
}
}
}
q.splice(0, q.length, ...nq);
dist++;
}
items.sort((a, b) => {
for (let i = 0; i < 4; ++i) if (a[i] !== b[i]) return a[i] - b[i];
return 0;
});
const ans: number[][] = [];
for (const [d, v, r, c] of items) {
if (ans.length === k) break;
ans.push([r, c]);
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(m*n*log(m*n)), where m and n are grid dimensions. BFS visits each cell once, and sorting all found items takes O(N log N) where N is the number of items. - 🧺 Space complexity:
O(m*n), for visited array, queue, and storing all valid items.