K Radius Subarray Averages Problem

Problem

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

• For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

Examples

Example 1:

Input:
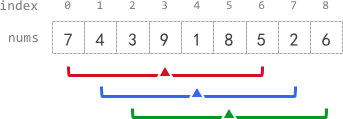
nums = [7,4,3,9,1,8,5,2,6], k = 3
Output:
 [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using **integer division**, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements **after** each index.

Example 2:

Input:
nums = [100000], k = 0
Output:
 [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input:
nums = [8], k = 100000
Output:
 [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

Constraints:

• n == nums.length
• 1 <= n <= 105
• 0 <= nums[i], k <= 105

Solution

Method 1 – Prefix Sum and Sliding Window

Intuition

To efficiently compute the average of every subarray of length 2k+1 centered at each index, we use a prefix sum array. This allows us to get the sum of any subarray in constant time. If there are not enough elements before or after an index, the answer is -1 for that index.

Approach

1. Initialize an answer array with -1 for all positions.
2. If 2k+1 > n, return the answer array (all -1).
3. Compute the prefix sum of the input array.
4. For each index i from k to n-k-1, compute the sum of the subarray from i-k to i+k using the prefix sum.
5. Set the average at index i as the integer division of the subarray sum by 2k+1.
6. Return the answer array.

Code

C++

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> ans(n, -1);
        if (2 * k + 1 > n) return ans;
        vector<long long> prefix(n + 1, 0);
        for (int i = 0; i < n; ++i) prefix[i + 1] = prefix[i] + nums[i];
        for (int i = k; i + k < n; ++i) {
            long long sum = prefix[i + k + 1] - prefix[i - k];
            ans[i] = sum / (2 * k + 1);
        }
        return ans;
    }
};

Go

func getAverages(nums []int, k int) []int {
    n := len(nums)
    ans := make([]int, n)
    for i := range ans {
        ans[i] = -1
    }
    if 2*k+1 > n {
        return ans
    }
    prefix := make([]int64, n+1)
    for i := 0; i < n; i++ {
        prefix[i+1] = prefix[i] + int64(nums[i])
    }
    for i := k; i+k < n; i++ {
        sum := prefix[i+k+1] - prefix[i-k]
        ans[i] = int(sum / int64(2*k+1))
    }
    return ans
}

Java

class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        int[] ans = new int[n];
        Arrays.fill(ans, -1);
        if (2 * k + 1 > n) return ans;
        long[] prefix = new long[n + 1];
        for (int i = 0; i < n; i++) prefix[i + 1] = prefix[i] + nums[i];
        for (int i = k; i + k < n; i++) {
            long sum = prefix[i + k + 1] - prefix[i - k];
            ans[i] = (int)(sum / (2 * k + 1));
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun getAverages(nums: IntArray, k: Int): IntArray {
        val n = nums.size
        val ans = IntArray(n) { -1 }
        if (2 * k + 1 > n) return ans
        val prefix = LongArray(n + 1)
        for (i in 0 until n) prefix[i + 1] = prefix[i] + nums[i]
        for (i in k until n - k) {
            val sum = prefix[i + k + 1] - prefix[i - k]
            ans[i] = (sum / (2 * k + 1)).toInt()
        }
        return ans
    }
}

Python

class Solution:
    def getAverages(self, nums: list[int], k: int) -> list[int]:
        n = len(nums)
        ans = [-1] * n
        if 2 * k + 1 > n:
            return ans
        prefix = [0]
        for num in nums:
            prefix.append(prefix[-1] + num)
        for i in range(k, n - k):
            s = prefix[i + k + 1] - prefix[i - k]
            ans[i] = s // (2 * k + 1)
        return ans

Rust

impl Solution {
    pub fn get_averages(nums: Vec<i32>, k: i32) -> Vec<i32> {
        let n = nums.len();
        let mut ans = vec![-1; n];
        let k = k as usize;
        if 2 * k + 1 > n {
            return ans;
        }
        let mut prefix = vec![0i64; n + 1];
        for i in 0..n {
            prefix[i + 1] = prefix[i] + nums[i] as i64;
        }
        for i in k..n - k {
            let sum = prefix[i + k + 1] - prefix[i - k];
            ans[i] = (sum / (2 * k + 1) as i64) as i32;
        }
        ans
    }
}

TypeScript

class Solution {
    getAverages(nums: number[], k: number): number[] {
        const n = nums.length;
        const ans = Array(n).fill(-1);
        if (2 * k + 1 > n) return ans;
        const prefix = [0];
        for (let i = 0; i < n; i++) prefix.push(prefix[prefix.length - 1] + nums[i]);
        for (let i = k; i + k < n; i++) {
            const sum = prefix[i + k + 1] - prefix[i - k];
            ans[i] = Math.floor(sum / (2 * k + 1));
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n), where n is the length of the array, since prefix sums and window averages are computed in linear time.
• 🧺 Space complexity: O(n), for the prefix sum array and answer array.